Функциональное программирование

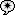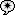Чистое `lambda`-исчисление – это исчисление анонимных функций, в нем отсутствуют константы, структуры данных и управляющие предложения. Но все эти возможности можно определить, используя `lambda`-выражения. Выражение в чистом `lambda`-исчислении имеет следующий синтаксис:

Все функции в `lambda`-исчислении имеют один аргумент, поэтому при применении функций используется карринг. Функция всегда применяется к самому левому аргументу, и скобки в вызове функции обычно не используются:

Вычисление `lambda`-выражений производится с помощью специальных правил вывода. `beta`-редукция заменяет вызов функции ее телом с заменой всех вхождений связанной переменной на выражение, соответствующее аргументу. `delta`-правила используются для вычисления базовых функций с достаточным количеством аргументов (если `lambda`-исчисление было расширено введением дополнительных типов данных и операций над ними, например, целые или вещественные числа). 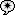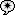Дополнительное `alpha`-преобразование выполняет переименование переменных таким образом, чтобы все связанные переменные в теле функции имели уникальные имена, и можно было применить `beta`-редукцию.

Выражение, которое можно преобразовать путем применения `beta`-редукции или `delta`-правила, называется редексом. Самым левым редексом называется редекс, символ `lambda` которого (или идентификатор базовой функции) расположен в `lambda`-выражении левее всех остальных редексов. Самым внешним редексом называется редекс, который не содержится внутри никакого другого редекса. Нормальный порядок редукций предписывает вначале преобразовывать самый левый из самых внешних редексов. Такой порядок соответствует ленивому вычислению.

Теперь рассмотрим, как основные возможности функциональных языков могут выражены средствами ?-исчисления. Условное предложение "`bb"если"\ p\ bb"то"\ q\ bb"иначе"\ r`" можно рассматривать как функцию, которая, используя значение `p`, выбирает одно из выражений `q` или `r`. Если функция `"TRUE"` будет возвращать свой первый аргумент, а функция `"FALSE"` – второй аргумент, то условный оператор выражается следующим образом:

Значения TRUE и FALSE представляются в виде:

Логические операции `"AND"`, `"OR"` и `"NOT"` можно выразить следующим образом:

Конструктор списка можно рассматривать как функцию, берущую в качестве своего аргумента функцию-селектор и применяющую ее к выражениям, соответствующим голове и хвосту списка:

Для выделения головы списка необходима функция-селектор `lambda\ h.\ lambda\ t.\ h`, а для хвоста – `lambda\ h.\ lambda\ t.\ t`, что в точности соответствует определениям `"TRUE"` и `"FALSE"`. Таким образом, определения функций выделения головы и хвоста списка могут быть определены следующим образом:

Функция проверки `"NULL"` должна `"TRUE"`, если список пустой, и `"FALSE"` в противном случае. То есть `"NULL"\ ("CONS"\ a\ b)` (т.е. `"NULL"\ (lambda\ s.\ s\ a\ b)`) должно давать `"FALSE"` для любых значений `a` и `b`. Выражение для `"NULL"` должно иметь вид:

А пустой список можно определить так:

Натуральное число `n` можно рассматривать `n`-элементный список из произвольных значений. Число 0 в этом представлении соответствует пустому списку `"NIL"`, функции сравнения с нулем (`"EQ"0`) и уменьшения числа на 1 (`"PRED"`) соответствуют функциям `"NULL"` и `"TAIL"`. Для увеличения числа на 1 будем использовать функцию `"SUCC"\ =\ lambda\ n.\ "CONS"\ (lambda\ x.\ x)\ n`.

Так как в `lambda`-исчислении функции не имеют имен, то для представления рекурсии необходим метод, позволяющий функциям вызывать себя не по имени, а каким-то другим способом. Можно представить рекурсивную функцию как функцию, имеющую саму себя в качестве аргумента. Например, функция сложения двух чисел `"add"(x,y)=(bb"если"\ x=0\ bb"то"\ y\ bb"иначе"\ "add"(x–1,y+1))` представляется в виде функции с дополнительным параметром:

Для вызова такой функции используется Y-комбинатор, удовлетворяющий уравнению Y f=f (Y f), который известен также как комбинатор фиксированной точки.

Одно из возможных определений Y-комбинатора имеет вид:

В правильности данного определения легко убедиться: `Y\ f` –> `(lambda\ h.\ (lambda\ x.\ h\ (x\ x))\ (lambda\ x.\ h\ (x\ x)))\ f` –> `(lambda\ x.\ f\ (x\ x))\ (lambda\ x.\ f\ (x\ x))` –> `f\ ((lambda\ x.\ f\ (x\ x))\ (lambda\ x.\ f\ (x\ x)))` = `f\ (Y\ f)`.

При вычислении `lambda`-выражений основной проблемой, снижающей эффективность, является порождение копии тела функции, чтобы заменить переменные соответствующими им выражениями. Комбинаторная логика позволяет избавиться от переменных и свести вычисление выражения к выполнению последовательности преобразований, определяемых комбинаторами.

Теоретически для представления любого `lambda`-выражения в комбинаторной логике достаточно двух комбинаторов – вычеркиватель `K\ =\ lambda\ x.\ lambda\ y.\ x` и распределитель `S\ =\ lambda\ f.\ lambda\ g.\ lambda\ x.\ f\ x\ (g\ x)`, – но обычно используются также тождественный комбинатор `I\ =\ lambda\ x.\ x`, комбинатор фиксированной точки Y, композитор `B\ =\ lambda\ f.\ lambda\ g.\ lambda\ x.\ f\ (g\ x)`, перестановщик `C\ =\ lambda\ f.\ \ lambda\ x.\ lambda\ y.\ f\ y\ x`, дубликатор `W\ =\ lambda\ x.\ lambda\ y.\ x\ y\ y` и другие. В качестве базиса в комбинаторной логике можно использовать наборы комбинаторов 1) K,S; 2) I,B,C,S; 3) B,W,K. Остальные комбинаторы можно выразить через другие, например, `I\ =\ S\ K\ K`.

Выражение в комбинаторной логике имеет следующий синтаксис:

Комбинаторы определены следующими правилами редукции:

Для преобразования `lambda`-выражения в комбинаторную форму можно использовать следующие правила:

Например, выражение `lambda\ x.\ lambda\ y.\ (+\ (times\ x\ y)\ 1)` соответствует формуле `S(S("KS")\ (S(K(S(K+)))\ times))\ (K(K\ 1))`. При частичном применении этой функции к аргументу 2 получаем формулу `S(S(K+)(times\ 2))(K\ 1)`. Использование дополнительных комбинаторов существенно уменьшает сложность получаемых выражений.

1. Оптимизируйте комбинаторную формулу для выражения `lambda\ x.\ \ lambda\ y.\ (+\ (times\ x\ y)\ 1)`, используя комбинаторы B и C, а также правила `S\ (K\ e_1)\ e_2\ ->\ B\ e_1\ e_2` и `S\ e_1\ (K\ e_2)\ ->\ C\ e_1\ e_2`.

2. Определите `lambda`-выражение для операции сравнения "больше" двух натуральных чисел.

3. Предложите `lambda`-представление для целых чисел.