Назад
 Начало Начало |
 Учебные материалы Учебные материалы |
Другие разделы
Дата и время
12/03/2026 21:24:04
 Функциональное программирование
Функциональное программирование
Функции и программирование Списки. Функции для работы со списками Определение новых функций Функции высших порядков и /\-выражения Представление и выполнение функциональных программ Виды вычислений. Карринг. Конвейеры. Запоминание. Монады Интерпретация и компиляция функциональных программ Функции высших порядков. Обозначение типа Чистое /\-исчисление. Комбинаторная логика
 Функции и программирование
Функции и программирование
Концепция функции является одним из фундаментальных понятий математики. Чтобы задать функцию `y=f(x)`, связывающую две переменные величины `x` и `y`, необходимо указать: 1) множество `A` значений, которые может принимать `x` (область определения функции), 2) множество `B` значений, которые может принимать `y` (область значения функции), 3) правило `f(x)`, по которому значениям `x` из `A` соотносятся значения `y` из `B`. Каждому элементу из области определения однозначная функция ставит в соответствие в точности один элемент из области значения. Правило в простейшем случае можно изобразить с помощью графа или с помощью таблицы (рис. 1).
а) 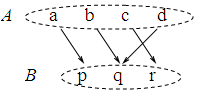 | б) 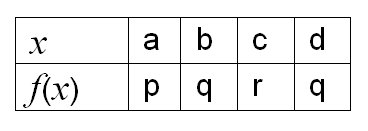 |
| Рис.1 | |
Чаще всего правило задается формулой, устанавливающей, какие вычислительные операции надо произвести над `x`, чтобы найти `y`: `"квадрат"(x)=x^2`. В этом определении область определения и область значений функции даны неявно и не всегда очевидны. Например, функция `"квадрат"` отображает множество вещественных чисел во множество неотрицательных вещественных чисел, а целые числа в неотрицательные целые числа.
Если есть элементы из области определения, для которых отображение посредством этой функции не определено, то функция называется частичной или частично определенной. Например, функция `"обратное"(x)=1/x` является частично определенной над множеством вещественных чисел. Функция, не являющаяся частичной, называется общей или всюду определенной.
Функцию нескольких аргументов можно рассматривать как функцию одного аргумента (кортежа), множество значений которого является декартовым произведением множеств значений всех аргументов функции. Другая интерпретация функции нескольких аргументов заключается в том, что применение функции `f` к аргументам `(a,b)` рассматривается как выражение `(f(a))(b)`, где результатом вызова функции `f` с аргументом `a` является новая функция `f\ '` с одним аргументом, которая затем вычисляется для аргумента `b`.
Некоторые функции на разных частях своей области определения задаются различными формулами, например:
`"макс"(x,y)={(x,text{если}\ x\ ≥\ y),(y,text{в противном случае}):}`Это правило удобнее записывать как `"макс"(x,y)=bb"если"\ x\ ≥\ y\ bb"то"\ x\ bb"иначе"\ y`. Условное предложение "если то иначе" позволяет выбрать одну из двух формул для вычисления результата функции в зависимости от некоторого условия. Часть предложения "иначе" не может быть опущена. При применении функции `"макс"` к аргументам `(1,3)` вычисление по данному правилу происходит так: параметрам функции `x` и `y` сопоставляются значения `1` и `3`, затем вычисляется значение выражения `x\ ≥\ y` (т.е. `1\ ≥\ 3`), что дает ложь, и в качестве результата функции возвращается значение `y` (т.е. `3`). Таким образом, вызов функции `"макс"(1,3)` дает результат `3`.
Важнейшим приемом в функциональном программировании является композиция функций, позволяющая определять одни функции через другие, например: `"макс"3(x,y,z)="макс"("макс"(x,y),z)`. Результат вызова функции `"макс"(x,y)` используется в качестве аргумента для функции `"макс"`.
Функциональная программа состоит из совокупности определений функций. Функции, в свою очередь, представляют собой вызовы других функций и предложения, управляющие последовательностью вызовов. Вычисления начинаются с вызова некоторой функции, которая, в свою очередь, вызывает функции, входящие в ее определение и т. д. в соответствии с иерархией определений и структурой условных предложений. Функции часто либо прямо, либо косвенно вызывают сами себя. В конечном итоге при вычислении функции должны ссылаться на основные базовые функции. Каждый вызов возвращает некоторое значение в вызвавшую его функцию, вычисление которой после этого продолжается; этот процесс повторяется до тех пор, пока запустившая вычисления функция не вернет конечный результат пользователю.
Рассмотрим следующую программу на языке Си:
double max(double x, double y)
{ if(x>=y)
return x;
else
return y;
}
С помощью данной функции легко найти максимум из трех значений, используя композицию:
m=max(max(a,b),c);
Можно определить функцию max и другим способом:
void max(double x, double y, double *z)
{ if(x>=y)
*z=x;
else
*z=y;
}
Понятие функции при этом не нарушается, но результат возвращается через один из аргументов. В этом случае для вычисления максимума из трех чисел невозможно использовать композицию, и результат может быть вычислен только с помощью последовательности вызовов:
max(a,b,&m); max(m,c,&m);
То же самое произойдет, если результат функции будет возвращаться через глобальную переменную. Такие особенности работы функции называются "побочными эффектами". Функция, не имеющая побочных эффектов, называется строгой.
Строго функциональный язык не допускает побочных эффектов, не признает присваивание и передачу управления. Разветвление вычислений основано на механизме обработки частей условного предложения. Повторяющиеся вычисления осуществляются через рекурсию. Единственным "эффектом" выполнения любой функции является вычисленный результат.
Так как нет присваивания, переменные, получив значение в начале блока вычислений, например, при вызове функции, больше никогда его не меняют. Таким образом, переменные – это просто сокращенная запись их значений, и на место переменных в программе всегда можно вставить выражения, по которым они вычисляются. Порядок проведения вычислений становится несущественным. Так как на результат вычислений не влияют никакие побочные эффекты, то неважно, когда вычислять этот результат.
Кроме того, функциональный язык обладает двумя мощными механизмами, позволяющими писать более краткие и универсальные программы. Во-первых, аргументами или результатом функции могут быть сложные структуры данных. Однажды построенная структура не может изменяться, но может включаться в другие. Во-вторых, можно определить функцию высшего порядка, аргументами или результатом которой является функции.

