Назад
 Начало Начало |
 Учебные материалы Учебные материалы |
Другие разделы
Дата и время
18/02/2026 06:21:50
 Функциональное программирование
Функциональное программирование
Функции и программирование Списки. Функции для работы со списками Определение новых функций Функции высших порядков и /\-выражения Представление и выполнение функциональных программ Виды вычислений. Карринг. Конвейеры. Запоминание. Монады Интерпретация и компиляция функциональных программ Функции высших порядков. Обозначение типа Чистое /\-исчисление. Комбинаторная логика
 Виды вычислений. Карринг. Конвейеры. Запоминание. Монады
Виды вычислений. Карринг. Конвейеры. Запоминание. Монады
Так как в функциональном программировании время вычисления значения выражения является несущественным, то аргументы функции можно вычислять либо до вызова функции, либо только тогда, когда значение этого аргумента потребуется внутри тела функции. Первый способ вычисления называется энергичным, его реализация является простой и эффективной. Второй способ называется ленивым, его реализация менее эффективная, так как в функцию передаются невычисленные выражения, но это позволяет избежать затрат на вычисления, если значение аргумента не потребуется. Языки LISP и Scheme используют энергичную семантику, а Haskell и Standard ML – ленивую. Для повышения эффективности можно использовать смешанный способ вычислений, который использует анализ тела функции. Функция, которая всегда требует значение одного из своих аргументов, является строгой по отношению к этому аргументу. Например, функция `f(x,y)=(bb"если"\ x>0\ bb"то"\ x\ bb"иначе"\ y)` является строгой по отношению к `x` и нестрогой по отношению к `y`.
Ленивые вычисления позволяют создавать и обрабатывать циклические и бесконечные последовательности (при этом известная часть последовательности хранится в памяти, а остальная часть хранится в виде формулы). Также ленивые вычисления помогают избежать лишних вычислений. Рассмотрим, например, функцию `"элемент"(x,s)="редукция"(s,\ lambda(e,t)\ bb"если"\ е=x\ bb"то"\ #T\ bb"иначе"\ t,\ #F)`. В языке с энергичной семантикой при вычислении выражения `"элемент"(2,\ '(2\ 7\ 1\ 8))` потребуется полная обработка списка, при использовании ленивых вычислений результат будет получен сразу и поиска элемента в оставшейся части списка не потребуется.
В языках с энергичной семантикой для работы с ленивыми вычислениями будем использовать операции "задержать" и "возобновить". Операция "задержать" создает функциональное замыкание из выражения и контекста, определяющего значения пе-ременных, входящих в это выражение. Результат можно рассматривать как функцию без параметров, функцию-константу. Операция "возобновить" позволяет вызвать эту функцию и получить значение выражения. Обычно операция "возобновить" сохраняет вычисленное значение, и, если снова потребуется это значение, повторное вычисление не делается, а используется результат предыдущего вычисления.
Бесконечную последовательность целых чисел можно задать следующим образом:
`"целоеот"(m)="cons"(m,\ bb"задержать"\ "целоеот"(m+1))`Для получения первых элементов бесконечной последовательности будем использовать следующую функцию:
`"первые"(k,x)=bb"если"\ k=0\ bb"то"\ '()\ bb"иначе"\ "cons"("car"(x),\ "первые"(k–1,\ bb"возобновить"\ "cdr"(x)))`Например, выражение `"первые"(5,"целоеот"(1))` возвращает список `(1\ 2\ 3\ 4\ 5)`. Выражение `"целоеот"(1)` возвращает результат `(1\ .\ ["целоеот"(m+1),\ {m\ ->\ 1}])`. При возобновлении вычисления хвоста списка будет получен результат `(2\ .\ ["целоеот"(m+1),\ {m\ ->\ 2}])`.
Ряд Фибоначчи можно определить следующим образом:
`"суммспис"(x,y)="cons"("car"(x)+"car"(y),\ bb"задержать"\ "суммспис"(bb"возобновить"\ "cdr"(x),\ bb"возобновить"\ "cdr"(y)))`;`"фиб"={bb"возобновить"\ a1`
`bb"гдерек"\ a1=bb"задержать"\ "cons"(1,\ a2)`;
`a2=bb"задержать"\ "cons"(1,\ a3)`;
`a3=bb"задержать"\ "суммспис"(bb"возобновить"\ a1,\ bb"возобновить"\ a2)}`
В языках с ленивой семантикой текст программы является более декларативным, так как исчезают операции, управляющие процессом вычислений. Например, так будет выглядеть вычисление последовательности простых чисел.
`"целоеот"(m)="cons"(m,\ "целоеот"(m+1))`;`"фильтр"(p,y)={bb"если"\ "car"(y)\ mod\ p=0\ bb"то"\ z\ bb"иначе"\ "cons"("car"(y),z)`
`bb"где"\ z="фильтр"(p,"cdr"(y))}`;
`"решето"(x)="cons"("car"(x),"решето"("фильтр"("car"(x),"cdr"(x)))`;
`"простые"="решето"("целоеот"(2))`
Используя ленивые вычисления, можно определять циклические структуры данных:
`"ones"="cons"(1,"ones")`; /* последовательность единиц */`"twins"="соединить"(‘(1\ 2),"twins")`; /* последовательность 1 2 1 2 … */
`"цикл"(x)={w\ bb"гдерек"\ w="отобр"(x,\ lambda(z)\ "cons"(z,w))}`
Также можно определять функции, в которых результат работы функции зависит от величин, которые неизвестны до тех пор, пока вычисление не закончено. Например, рассмотрим функцию, заменяющую каждый элемент в числовом списке максимальным элементом этого списка. В энергичном языке два просмотра списка, сначала, чтобы найти максимальное значение, затем для замены элементов списка. Ленивая семантика допускает более простое решение.
`"заменить"(s)={"car"(v)\ ``bb"гдерек"\ v="редукция"(s,f,"cons"(‘(),"car"(s)));`
`f=lambda(x,y)\ "cons"("cons"(m,"car"(y)),\ bb"если"\ x>"cdr"(y)\ bb"то"\ x\ bb"иначе"\ "cdr"(y));`
`m="cdr"(v)}`
Функцию нескольких аргументов можно рассматривать как суперпозицию функций одного аргумента, например, функцию `"plus"=lambda(x,y)\ x+y` можно интерпретировать как `"plus"=lambda(x)lambda(y)\ x+y`. Вызов `"plus"(1,2)` интерпретируется как последовательность вызовов `("plus"(1))(2)`. Сначала применяется первый аргумент `"plus"(1)`, в результате получается новая функция `lambda(y)1+y`. Эта функция применяется ко второму аргументу `(lambda(y)1+y)(2)`, и получается окончательный результат 3. Такой способ обработки функции нескольких аргументов называется каррингом (currying) по имени математика Х. Карри.
Вызов функции с меньшим числом аргументов, чем указано в определении функции, результатом которого является новая функция, называется частичным применением. Частичное применение позволяет уменьшить число определяемых функций, определять более гибкие и мощные функции.
`"комп"(f,g)=lambda(x)\ f(g(x))`;`"отобр"(f,x)="редукция"(x,\ "комп"("cons",f),\ '())`;
`"плюс"(x,y)=x+y`;
`"увел"1="отобр"("плюс"(1))`
Вызов `"комп"("cons",f)` возвращает функцию, которая при применении к какому-либо аргументу возвращает новую функцию, которая сцепляет результат вычислений со своим аргументом. Таким образом, функция `"отобр"` легко определяется через функцию `"редукция"` с помощью частичного применения.
Пусть у нас есть функции `"фильтр"(f,s)`, `"отобр"(f,s)` и `"сорт"(s)` и мы хотим выбрать все четные элементы некоторого списка, отсортировать их и возвести в квадрат. Это можно сделать с помощью выражения:
`"отобр"(lambda(x)x*x,\ "сорт"("фильтр"(lambda(x)x\ mod\ 2=0,\ '(5\ 10\ 8\ 3\ 6\ 12))))`что выглядит не слишком понятно из-за большого количества скобок и необходимости чтения порядка действий справа налево. При использовании конвейера аргумент указывается слева от вызова функции, а её результат может быть отправлен в следующую функцию на конвейере. Количество и вложенность скобок при этом резко уменьшается, а порядок выполнения действий становится естественным – слева направо:
`'(5\ 10\ 8\ 3\ 6\ 12)\ |\ "фильтр"(lambda(x)x\ mod\ 2=0)\ |\ "сорт"\ |\ "отобр"(lambda(x)x*x)`Запоминание предыдущих значений аргументов, к которым применялась функция, и полученных при этом результатов в специальной таблице позволяет не вычислять результат заново для тех же аргументов, а использовать ранее вычисленный. Корректность результата такой мемо-функции гарантируется отсутствием побочных эффектов в функциональных языках. Рассмотрим функцию `"power"`, вычисляющую `2^n`.
`"power"(n)=bb"если"\ n=0\ bb"то"\ 1\ bb"иначе"\ "power"(n–1)+"power"(n–1)`При обычной реализации вычисление потребует `2^n+1` вызовов функции `"power"`. Если же `"power"` будет мемо-функцией, то второй вызов в ее определении сведется к простому поиску полученного ранее результата в таблице, и рекурсивные вызовы не потребуются. Таким образом, будет сделано лишь `n+1` вызовов, и время выполнения этого неоптимального решения существенно уменьшится.
Обычно в качестве мемо-таблицы используется таблица хеширования или двоичные деревья, а аргументы сравниваются не на полное совпадение, а на идентичность адресов. Адрес аргумента используется как ключа для поиска в таблица. Это особенно удобно для ленивых вычислений, так как это позволяет определять результат функции даже без вычисления аргументов. Запоминание существенно упрощает обработку бесконечных циклических структур.
`"отобр"(x,f)=bb"если"\ "null"(x)\ bb"то"\ '()``bb"иначе"\ "cons"(f("car"(x)),"отобр"("cdr"(x),f))`;
`"ones"="cons"(1,"ones")`;
`"double"(x)=2*x`;
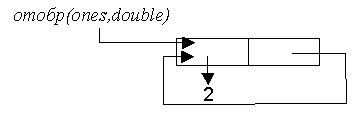
`"twos"="отобр"("ones",\ "double")`
Для создания структуры `"twos"` потребуется конечное время и конечный объем памяти, так как второй вызов функции `"отобр"` вернет указатель на вычисленное ранее значение (рис. 3).
Во многих языках программирования порядок вычислений частей выражения не фиксируется, а в языках с ленивой семантикой тем более.
Например, результат выполнения оператора выводЧисла(вводЧисла()-вводЧисла()); будет неопределен.
В процедурных языках (в том числе мультипарадигменных языках, таких как Kotlin) можно указать нужный порядок вычислений, используя конструкцию последовательности.
x=вводЧисла(); y=вводЧисла(); выводЧисла(x-y);
В языке Scheme также можно указать несколько последовательных действий в let, а его результатом является значение последнего выражения:
(let ((x (read))(y (read))) (display (- x y)) (newline))
Чтобы организовать линейную цепочку связанных вычислений и избежать сложностей с описанием того, что функции ввода-вывода имеют побочные эффекты, в функциональном языке с ленивой семантикой используются монады.  Аналогичная программа на языке Haskell будет выглядеть следующим образом:
Аналогичная программа на языке Haskell будет выглядеть следующим образом:
 Аналогичная программа на языке Haskell будет выглядеть следующим образом:
Аналогичная программа на языке Haskell будет выглядеть следующим образом:import IO
main = do
x <- вводЧисла
y <- вводЧисла
выводЧисла (x-y)
Кроме монады IO (строго последовательные вычисления), в Haskell используется монады State (вычисления с переменной состояния), Maybe (вычисления с отсутствующими значениями), List (вычисления с несколькими результатами) и другие.
Для реализации монад используются следующие идеи. При выполнении композиции вызовов `f(g(x))` результат выражения `g(x)` гарантированно будет вычислен до вычисления результата функции `f`. Состояние потоков ввода-вывода можно представить как дополнительное значение, которое передается в качестве аргумента функции и добавляется к результату. Операторы блока "do" превращаются компилятором языка Haskell в `lambda`-выражения, которым в качестве параметра передается структура с текущим состоянием потоков ввода-вывода и текущими значениями переменных.
`{bb"пусть"` `"op"1=lambda(a)"вводЧисла"(a)`
`"op"2=lambda(b)"cons"("car"(b),"вводЧисла"("cdr"(b)))`
`"op"3=lambda(c)"выводЧисла"("cddr"(c),"car"(c)-"cadr"(c))`
`в\ lambda("IO")"op"3("op"2("op"1("IO")))}`
Предполагается, что функция `"вводЧисла"` возвращает точечную пару из введенного числа и нового состояния потоков ввода-вывода, а `"выводЧисла"` – новое состояние потоков ввода-вывода.
Упражнения
1. Определите генератор случайных чисел, используя бесконечную последовательность `x_{i+1}=(8413453205*x_i+99991)\ mod\ 2^40`.
2. Определите бесконечную последовательность из чисел вида `1/(i!)`, начиная с `i=0`.
3. Определите функцию, вычисляющую сумму бесконечной последовательности с точностью `epsilon`.
4. Определите функцию слияния двух бесконечных возрастающих последовательностей. Одинаковые элементы последовательностей должны войти в список-результат только один раз.
5. Используя функцию слияния, определите возрастающую последовательность из элементов множества S, которое определяется следующим образом: `1\ ∈\ S`; если `x\ ∈\ S`, то `2*x+1\ ∈\ S` и `3*x+1\ ∈\ S`.
6. Определите возрастающую последовательность из чисел вида `2^k3^m5^n`, где `k,m,n\ ≥\ 0`. Первыми элементами этой последовательности являются 1 2 3 4 5 6 8 9 10 12.

