Подразделы

Другие разделы

Дата и время

01/04/2025 07:06:27

Авторизация

Структуры данных на основе деревьев

Определения Обходы бинарного дерева Двоичное дерево поиска Система непересекающихся множеств Сбалансированные деревья Декартово дерево Декартово дерево по неявному ключу Дерево отрезков

Дерево отрезков

Дерево отрезков — структура данных, позволяющая находить значение некоторой ассоциативной функции $f$ на произвольном отрезке $a_i, a_{i + 1},..., a_j$ массива за асимптотику $O(log N)$ . В качестве $f$ можно взять сумму, максимум или минимум. Изменять элементы (увеличивать, умножать, присваивать новое значение) можно также на отрезке за $O(log N)$ . Можно комбинировать несколько операций изменения и функций.

Для обеспечения указанной эффективности над массивом надстраивается пирамида, каждый элемент которой содержит результат вычислений функции для двух элементов ниже (и рекурсивно для всего поддерева) и "отложенную" операцию, которая применяется к этому результату.

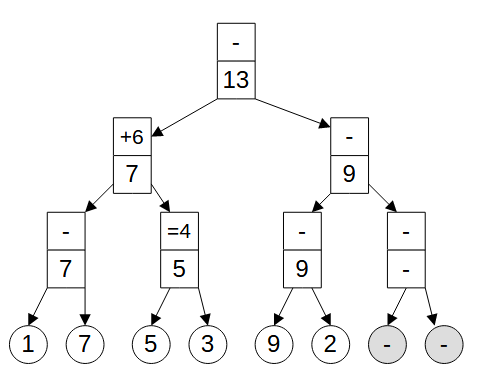
width:300px|stree

В нижнем слое пирамиды (листья бинарного дерева) находятся значения типа T, в остальных слоях – пара значений из типов Operation и State, у которого должен быть определен конструктор-преобразователь из типа T и конструктор по умолчанию, возращающий нейтральный элемент для функции $f$ . Функция $f$ принимает два значения типа State и возвращает значение типа State. "Отложенная" операция – это тип, у которого должны быть определены три метода:

struct Operation {
  State operator()(State s, size_t k) const;
  T operator()(T v) const;
  optional<Operation> combine(Operation other) const;
}

Если операции изменения выполняются только над одним элементом, то можно обновлять пирамиду снизу вверх. В общем случае операция изменения спускается сверху вниз, пока она будет соответствовать поддереву целиком, где она комбинируется с операцией, которая уже применена к этому поддереву, а при возврате из рекурсии обновляется поле State родительских вершин в пирамиде.

Указатели на дочерние вершины можно не хранить, если воспользоваться уже рассмотренным приемом для хранения пирамиды в массиве. Дочерние вершины для вершины $i$ имеют номера $2*i$ и $2*i+1$ , а родительская – номер $|__ i//2 __|$ . Вершина пирамиды находится в элементе массива с индексом 1.

template <typename T, typename State, typename Operation>
class STree {
using func=function<State(State,State)>;
size_t n,n2;
vector<pair<optional<Operation>,State>> pyrmd;
vector<T> values;
func f;
void update(size_t i, size_t k1, size_t k2) {
  if(i>=n2) return; // не применяется к листу
  pyrmd[i].second=f(state(2*i,k1),state(2*i+1,k2)); // обновляем состояние поддерева
}
void add_op(size_t i, Operation op) { // добавить или применить операцию
  if(i>=n2) values[i-n2]=op(values[i-n2]); // применить к листу
  else if(!pyrmd[i].first) pyrmd[i].first=op;
  else pyrmd[i].first=pyrmd[i].first->combine(op);
}
void clear_op(size_t i, size_t k) { // сдвинуть операцию вниз
  if(i>=n2 || !pyrmd[i].first) return;
  Operation op=*(pyrmd[i].first);
  pyrmd[i].second=op(pyrmd[i].second,k);
  pyrmd[i].first={};
  add_op(2*i,op);
  add_op(2*i+1,op);
}
State state(size_t i, size_t k) { // состояние поддерева или листа
  if(i>=n2) {
    if(i-n2>=n) return State();
    return State(values[i-n2]);
  }
  if(pyrmd[i].first) return (*(pyrmd[i].first))(pyrmd[i].second,k);
  return pyrmd[i].second;
}
State calc(size_t p, size_t k, size_t pi, size_t pj, size_t i, size_t j) {
  if(k==1) return State(values[p-n2]); // лист
  if(i<=pi && pj<=j) // все поддерево
    return state(p,pj+1-pi);
  clear_op(p,pj+1-pi); // сдвинуть операцию
  k/=2;
  size_t m=pi+k;
  // вернуть из одного поддерева
  if(j<m) return calc(p*2,k,pi,m-1,i,j);
  if(i>=m) return calc(p*2+1,k,m,pj,i,j);
  // или комбинацию
  return f(calc(p*2,k,pi,m-1,i,j), calc(p*2+1,k,m,pj,i,j));
}
void apply(size_t p, size_t k, size_t pi, size_t pj, size_t i, size_t j, optional<Operation> op, T v) {
  if(k==1) { // лист
    if(op) values[p-n2]=(*op)(values[p-n2]); 
    else values[p-n2]=v;
    return;
  }
  if(i<=pi && pj<=j) // полный отрезок 
  { if(op) add_op(p,*op);
    return;
  }
  clear_op(p,pj+1-pi); // сдвинуть операцию
  k/=2;
  size_t m=pi+k;
  if(i<m) // обработать поддеревья, если есть
    apply(p*2,k,pi,m-1,i,j,op,v);
  if(j>=m) 
    apply(p*2+1,k,m,pj,i,j,op,v);
  update(p,min(pj+1,m)-pi,max((int)(pj+1-m),0)); // пересчитать
}
public:
STree(size_t n, func f):n(n),n2(bit_ceil(n-1)),pyrmd(n2,{{},State()}),values(n,T()),f(f) {}
size_t size() const { return n; } // размер
State calc(size_t i, size_t j) { // получить значение функции на отрезке
  if(i>=n || j>=n || i>j) throw runtime_error("Wrong index");
  return calc(1,n2,0,n-1,i,j);
}
T get(size_t i) { // получить i-й элемент
  if(i>=n) throw runtime_error("Wrong index");
  size_t p=1, k=n2, a=0, b=n;
  while(p<n2) // бинарный поиск, пока не дойдем до листа
  { clear_op(p,b-a);
    k/=2;
    size_t m=a+k;
    if(i<m) {
      p=2*p;
      b=m;
    }
    else {
      p=2*p+1;
      a=m;
    }
  }
  return values[p-n2];
}
void set(size_t i, T v) { // изменить i-й элемент
  if(i>=n) throw runtime_error("Wrong index");
  apply(1,n2,0,n-1,i,i,{},v);
}
void apply(size_t i, size_t j, Operation op) { // изменить значения на отрезке
  if(i>=n || j>=n || i>j) throw runtime_error("Wrong index");
  apply(1,n2,0,n-1,i,j,op,T());
}
};

В декартовом дереве по неявному ключу уже подсчитывается количество элементов в поддереве. Можно добавить еще несколько полей, которые будут рассчитываться при разрезании и слиянии дерева. Также можно сохранять операции, которые применяются ко всему поддереву. Преимуществом дерева отрезков на дерамиде по сравнению с реализацией на массиве фиксированного размера является возможность удаления и вставки значений.