Начало
Учебные материалы
Структуры данных на основе деревьев
Определения Обходы бинарного дерева Двоичное дерево поиска Система непересекающихся множеств Сбалансированные деревья Декартово дерево Декартово дерево по неявному ключу Дерево отрезков
Система непересекающихся множеств
Операция|Эффективность|Вызов
--|--|--
конструктор (пустой набор)\
(n элементов) | `O(1)`\
`O(n)` | ``DSU d;``\
``DSU d(n);``
количество множеств | `O(1)` | ``auto k=d.count();``
количество элементов | `O(1)` | ``auto n=d.size();``
количество элементов в множестве | `O(1)` | ``auto k=d.size(id);``
добавить элемент | `O(1)` | ``auto id=d.add();``
идентификатор множества| `O(alpha(n))` | ``auto ids=d.set(id);``
проверка принадлежности одному множеству| `O(alpha(n))` | ``if(d.set(id1)==d.set(id2))...``
объединение множеств| `O(alpha(n))` | ``d.union(id1,id2);``
Здесь `alpha(n)` -- обратная функция Аккермана, даже для очень больших `n` не более 4. В качестве идентификатора множества выступает один из элементов этого множества. Первоначально все элементы образуют множества, включающие только сам элемент.
```c++
DSU d(6); // {0} {1} {2} {3} {4} {5}
d.union(1,3); // {0} {1,3} {2} {4} {5}
d.union(0,4); // {0,4} {1,3} {2} {5}
d.union(4,5); // {0,4,5} {1,3} {2}
cout<<d.count()<<"\n"; // 3
cout<<d.set(3)<<"\n"; // 1 (или 3)
cout<<(d.set(0)==d.set(1))<<"\n"; // 0 - в разных множествах
```
Удобно представить множества в виде леса деревьев
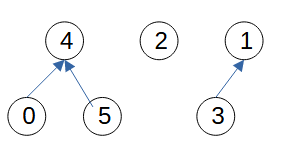
Достаточно хранить только указатель на родительскую вершину, так как элемент в корень дерева можно использовать в качестве идентификатора множества. Если вместо указателя хранить номер родительской вершины, то узлы леса деревья можно отобразить на массив целых чисел. Значение элемента можно заменить индексом элемента массива, и можно хранить только одно число -- номер родителя.
Для дерева возникает задача быстро находить его корень. При поиске корня все пройденные вершины можно переподвесить к корню, таким образом при следующих запросах длина пути сократится, в том числе у дочерних вершин на пройденном пути (сжатие пути).
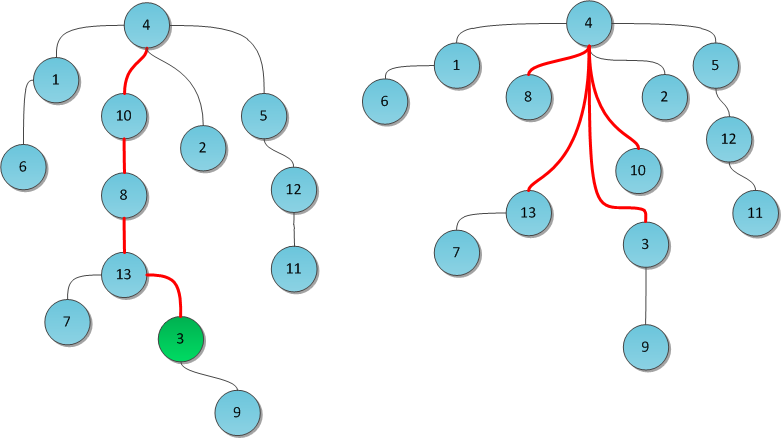
Еще одной полезной эвристикой является подвешивание дерева меньшей высоты к дереву большей высоты при объединении множеств: даже без сжатия пути оценка высоты дерева будет `O(log n)`. Но так как сжатие пути меняет высоту дерева, хранение этой информации и поддержание её в актуальном состоянии является бессмысленной тратой ресурсов. С другой стороны, при объединении множеств может получиться цепочка длины `n`. Хотя её сократит первый же запрос идентификатора множества, указанная оценка `O(alpha(n))` является амортизированной для `n` запросов, а для однократного запроса в худшем случае получается эффективность `O(n)`. Для уменьшения вероятности такой ситуации можно случайно выбирать какое дерево к какому присоединять, тогда математическое ожидание высоты дерева будет равно `4*log_2 n`. Или, если в DSU поддерживаются размеры множества, то можно множество меньшего размера присоединять к большему.
```
class DSU { // Система непересекающихся множеств
int n; // количество множеств
vector<int> p; // номер родителя
vector<int> s; // количество элементов в множестве
public:
DisjointSet(int n=0):n(n),p(n,-1),s(n,1) {}
int count() const { return n; } // количество непересекающихся множеств
int size() const { return p.size(); } // количество элементов
int size(int c) const { return s[set(c)]; } // количество элементов в множестве c
int add() { p.push_back(-1); s.push_back(1); return p.size()-1; } // добавить элемент
int set(int c) // к какому множеству принадлежит?
{ if(p[c]==-1) return c; // это корень?
return p[c]=set(p[c]); // присоединить узел к корню
}
void union(int a, int b) // соединить два множества
{ int pa=set(a), pb=set(b);
if(pa==pb) return; // уже соединены
if(s[pa]>s[pb]) // чтобы не допускать слишком высоких деревьев или if(rand()&1)
swap(pa,pb);
p[pa]=pb;
s[pb]+=s[pa];
n--;
}
};
```
[Применения](http://e-maxx.ru/algo/dsu)
* Нахождение компонент связности (как сильной, так и слабой)
* Наименьший общий предок в дереве
* Проверка двудольности графа онлайн
* Поиск мостов в графе онлайн
