 Структуры данных на основе деревьев
Структуры данных на основе деревьев
Определения Обходы бинарного дерева Двоичное дерево поиска Система непересекающихся множеств Сбалансированные деревья Декартово дерево Декартово дерево по неявному ключу Дерево отрезков
 Двоичное дерево поиска
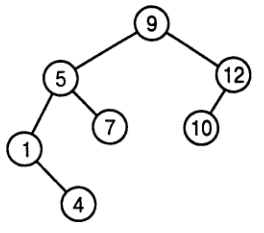
Двоичное дерево поиска
больше, чем число, назначенное ее левому потомку, и меньше, чем
число, назначенное ее правому потомку.
--
Реализация
```c++
template <typename T>
class BST {
public:
struct Node {
T key; // ключ
Node *left=nullptr, // левое поддерево
*right=nullptr, // правое поддерево
*parent=nullptr; // родитель (опционально)
Node(T key):key(key){}
};
Node* search(T key) const // поиск
{ Node *n=root;
while(n && key!=n->key)
{ if(key<n->key)
n=n->left;
else n=n->right;
}
return n;
}
...
private:
Node* root=nullptr;
};
```
--
```
Node* lower_bound(T key) const // поиск равного или большего ключа
{ Node* r=nullptr, *n=root;
while(n)
{ if(n->key<key)
n=n->right;
else
{ r=n;
n=n->left;
}
}
return r;
}
```
--
Обход дерева поиска - *внутренний итератор*. Время обхода `O(N)`.
```c++
private:
void inorder(Node* n, function<void(T)> fun) const
{ if(!n) return;
inorder(n->left,fun);
fun(n->key);
inorder(n->right,fun);
}
public:
void visit(function<void(T)> fun) const
{ inorder(root,fun);
}
...
// использование
BST<int> tree;
...
tree->visit([&](int k)->void { cout<<k<<" "; });
```
--
Обход дерева поиска -- *внешний итератор*.
```c++
Node* minim(Node* n) const // минимальный в поддереве
{ if(n)
while(n->left)
n=n->left;
return n;
}
Node* begin() const { // первый узел (минимальный в дереве)
return minim(root);
}
Node* next(Node* n) const { // следующий
while(n)
{ if(n->right)
{ n=minim(n->right);
break;
}
if(n->parent)
{ if(n->parent->left==n)
return n->parent;
}
n=n->parent;
}
return n;
}
// использование
BST<int> tree;
...
for(auto n=tree.begin();n;n=next(n))
print(n->key);
```
Переход за `O(log N)` в худшем случае. Суммарное время обхода с использованием указателя на родителя `O(N)`. Цикл по внешнему итератору легче прервать досрочно, можно комбинировать несколько внешних итераторов (например, сделать слияние двух BST), но работает медленнее внутреннего итератора.
--
Без указателя на родительскую вершину (для дерева без повторяющихся ключей). Суммарное время обхода -- `O(N log N)`.
```c++
Node* next(Node* n) const
{ Node *r=nullptr, *c=root;
int key=n->key;
while(c)
{ if(key<c->key)
{ r=c;
c=c->left;
}
else c=c->right;
}
return r;
}
```
Добавление (для мультимножества убрать проверку if(key<n->key) )
```c++
private:
void insert(Node*& n, T key, Node* p /* родительский узел */)
{ if(!n)
{ n=Node(value);
n->parent=p;
}
else if(n->key<key)
insert(n->right,key,n);
else if(key<n->key)
insert(n->left,key,n);
}
public:
void insert(T key) // вставка ключа
{ insert(root, key, nullptr);
}
```
--
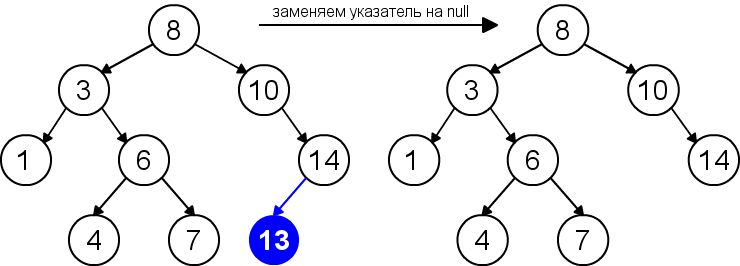
Удаление листа
--
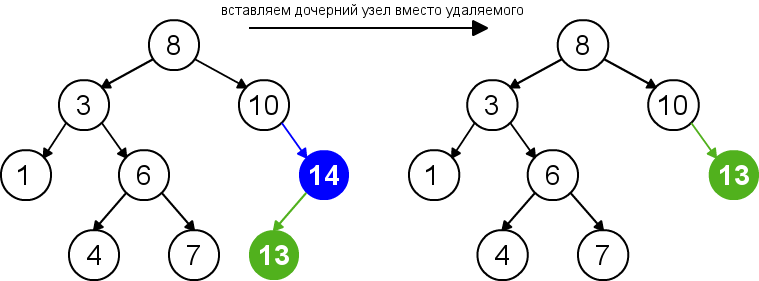
Удаление узла без правого поддерева
--
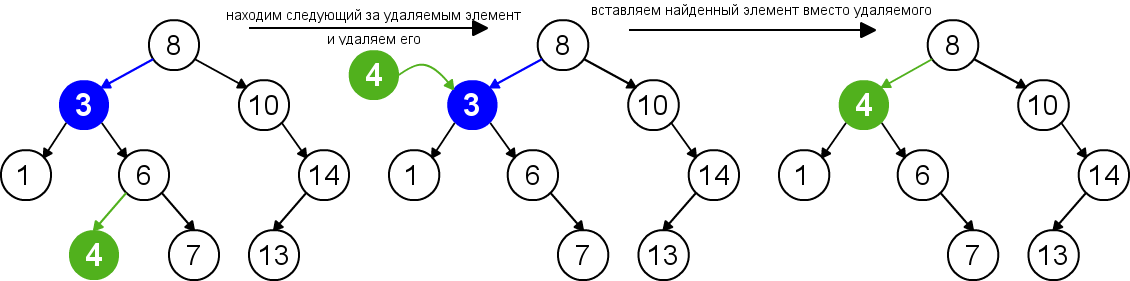
Удаление узла с правым поддеревом
--
```c++
private:
void erase(Node*& n, T key)
{ if(!n) return;
if(key<n->key) erase(n->left,key);
else if(key>n->key) erase(n->right,key);
else if(n->left && n->right)
{ n->key=minim(n->right)->key;
erase(n->right,n->key);
}
else
{ if(n->left)
n=n->left;
else if(n->right)
n=n->right;
else
n=nullptr;
}
}
public:
void erase(T key) // удаление ключа
{ erase(root, key);
}
```
Недостаток -- при создании BST из упорядоченной последовательности вместо дерева может получиться список и время поиска будет `O(n)`.

 Начало
Начало Учебные материалы
Учебные материалы