Подразделы

Другие разделы

Дата и время

01/04/2025 16:07:09

Авторизация

Структуры данных на основе деревьев

Определения Обходы бинарного дерева Двоичное дерево поиска Система непересекающихся множеств Сбалансированные деревья Декартово дерево Декартово дерево по неявному ключу Дерево отрезков

Декартово дерево

Декартово дерево — это структура данных, объединяющая в себе бинарное дерево поиска и бинарную кучу (treap = tree + heap, дерамида = дерево + пирамида), была предложена Сиделем и Арагоном в 1996 г.

Дерамида – это бинарное дерево, в узлах которого хранятся пары $(x,y)$ , где $x$ — это ключ, а $y$ — это приоритет. Оно является бинарным деревом поиска по $x$ и пирамидой по $y$ . Предполагая, что все $x$ и все $y$ являются различными, получаем, что если некоторый элемент дерева содержит $(x_0,y_0)$ , то у всех элементов в левом поддереве $x<x_0$ , у всех элементов в правом поддереве $x>x_0$ , а также и в левом, и в правом поддереве имеем: $y<y_0$ .

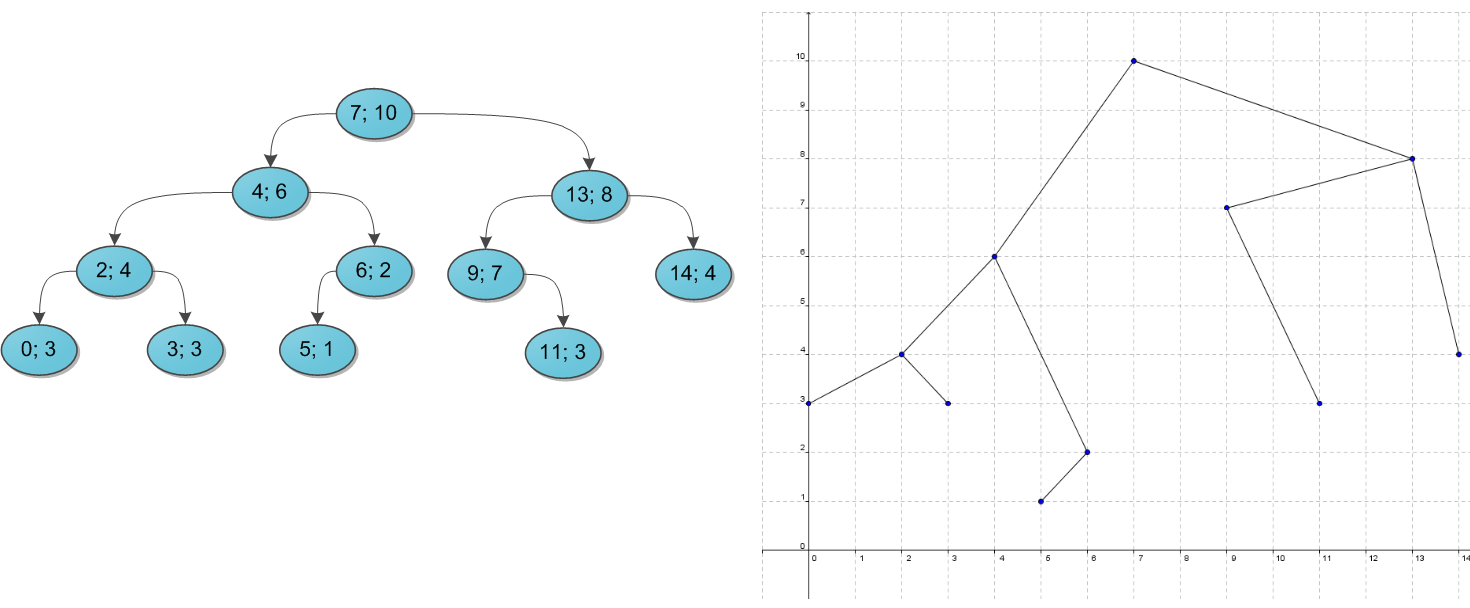
Почему дерево называется декартовым? Попробуем его нарисовать. Возьмем какой-нибудь набор пар «ключ-приоритет» и расставим на координатной сетке соответствующие точки $(x, y)$ . А потом соединим соответствующие вершины линиями, образуя дерево. Таким образом, декартово дерево отлично укладывается на плоскости благодаря своим ограничениям, а два его основных параметра — ключ и приоритет — в некотором смысле, координаты.

width:900px|дерево

Если бы приоритетов $y$ не было, то это было бы обычное бинарное дерево поиска по $x$ , и в зависимости от порядка добавления значений можно построить разные деревьев, в том числе вырожденные (в виде цепочки), в которых поиск выполнялся бы за $O(N)$ .

После добавления приоритетов из данных пар (x,y) можно построить единственное дерево, вне зависимости от порядка поступления ключей.

Если в качестве приоритета $y$ будем использовать случайное число, тогда полученное декартово дерево с очень высокой вероятностью будет иметь высоту, не превосходящую $4*log_2 N$ . И хоть оно не является сбалансированным (даже по сравнению с красно-черным деревом, в котором высота гарантированно не превышает $2*log_2 N$ ), математическое ожидание времени поиска ключа в таком дереве равно $O(log_2 N)$ .

Декартово дерево имеет следующие преимущества:

Проще реализуется по сравнению с настоящими самобалансирующимися деревьями.
Хорошо ведёт себя «в среднем», если ключи $y$ раздать случайно.
Типичная для сортирующего дерева операция «разделить по ключу на „меньше $k$ “ и „не меньше $k$ “» выполняется тривиально, а на красно-чёрных деревьях придётся восстанавливать балансировку и окраску узлов.

template <typename Key>
class Treap {
struct node {
  Key x; // ключ (координата x)
  int y; // случайная высота
  node *left=nullptr, // указатель на левое поддерево
     *right=nullptr; // указатель на правое поддерево
  node(Key x) : x(x), y(rand()) {}
};
node* root;
void free(node *t) { // освобождение
  if(!t) return; 
  // обратный обход
  free(t->left);
  free(t->right);
  delete t;
}
public:
Treap():root(nullptr) {}
Treap(const Treap&)=delete; // запрет копирования
Treap& operator=(const Treap&)=delete; // запрет присваивания
~Treap() { free(root); }
...

Основные операции

private:
void inorder(node* n, function<void(Key)> fun) const
{ if(!n) return;
  inorder(n->left,fun);
  fun(n->x);
  inorder(n->right,fun);
}
public:
void visit(function<void(Key)> fun) const // обход дерева
{ inorder(root,fun);
}
bool contains(Key k) const { // поиск как у всех BST
  node *n=root;
  while(n)
  { if(k<n->x)
      n=n->left;
    else if(n->x<k)
      n=n->right;
    else return true;
  }
  return false;
}

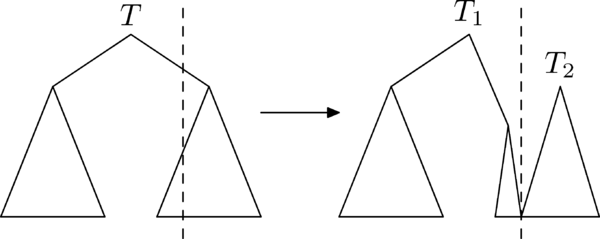
Операция разрезать исходное дерево $T$ по ключу $k$ возвращает пару деревьев $(T_1,T_2)$ , что в дереве $T_1$ ключи меньше $k$ , а в дереве $T_2$ все остальные.

split

private:
pair<node*, node*> split(node* t, function<bool(node*)> cond /* условие разделения */) {
  if (!t) return {nullptr,nullptr};
  if (cond(t)) {
    auto [t1,t2]=split(t->right,cond);
    t->right=t1;
    return {t,t2};
  } else {
    auto [t1,t2]=split(t->left,cond);
    t->left=t2;
    return {t1,t};
  }
}

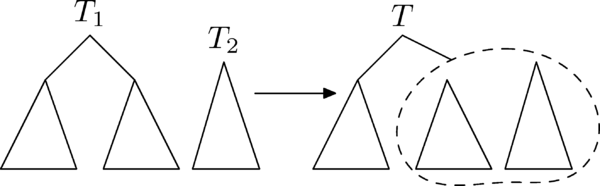
Операция слить соединяет пару деревьев $(T_1,T_2)$ в одно.

merge

private:
node* merge(node* t1, node* t2) {
  if(!t2) return t1;
  if(!t1) return t2;
  if (t1->y > t2->y) {
    t1->right=merge(t1->right,t2);
    return t1;
  } else {
    t2->left=merge(t1,t2->left);
    return t2;
  }
}

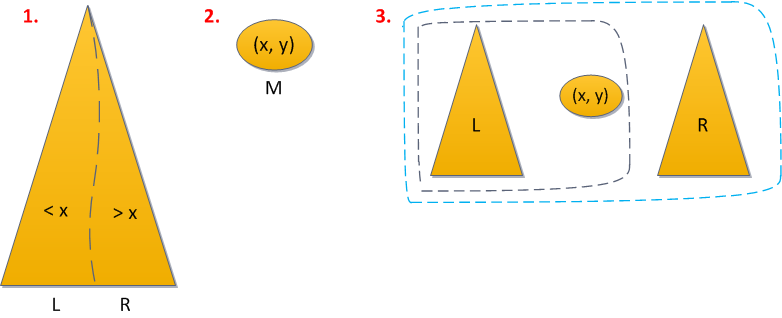
Добавление реализуется с помощью этих операций:

Разделим (split) дерево по ключу $x$ на дерево $L$ , с ключами меньше $x$ , и дерево $R$ , с большими $x$ .
Создадим из данного ключа дерево $M$ из единственной вершины $(x, y)$ , где $y$ — только что сгенерированный случайный приоритет.
Объединим (merge) по очереди $L$ с $M$ , то что получилось — с $R$ .

width:800px|add

public:
void insert(Key k) {
   if(contains(k)) return;
   auto [t1,t2]=split(root,[=](node *t){ return t->x<k; });
   node *m=new node(k);
   root=merge(merge(t1,m),t2);
}

Удаление реализуется аналогично:

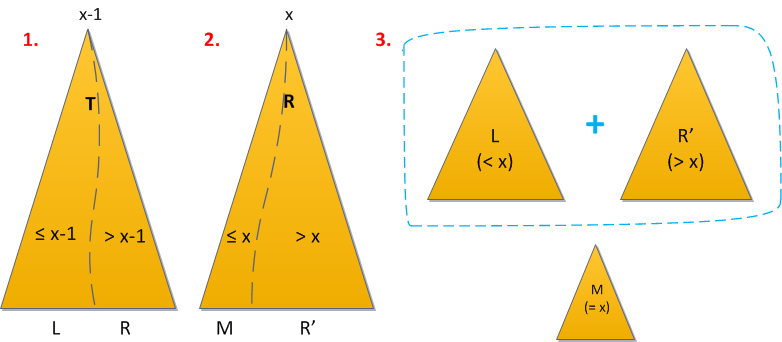
Разделим сначала дерево по ключу $x$ . Все элементы, меньшие $x$ , отправились в левый результат, значит, искомый элемент — в правом.
Разделим правый результат так, чтобы в новый правый результат отправились все элементы с ключами, большими $x$ , а в «средний» (левый от правого) — все меньшие либо равные $x$ . Но поскольку строго меньшие после первого шага все были отсеяны, то среднее дерево и есть искомый элемент.
Теперь просто объединим снова левое дерево с правым, без среднего, и дерамида осталась без ключей $x$ .

width:800px|del