Начало
Учебные материалы
Метод преобразования
Идея метода преобразования Предварительная сортировка Метод исключения Гаусса Пирамиды и пирамидальная сортировка Схема Горнера Приведение задачи
Пирамиды и пирамидальная сортировка
частично упорядоченную структуру данных, которая в особенности
хорошо подходит для реализации *очередей с приоритетами*.
В очереди с приоритетами каждый элемент
имеет характеристику, называемую *приоритетом*, и обеспечивает выполнение следующих операций:
* поиск элемента с наивысшим (т.е. с наибольшим) приоритетом;
* удаление элемента с наибольшим приоритетом;
* добавление нового элемента в множество.
--
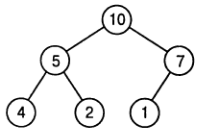
Пирамида определяется как бинарное дерево
с ключами, назначенными ее узлам (по одному ключу на узел), для которого
выполняются два следующих условия:
1. Требование к форме дерева. Бинарное дерево практически полное,
т.е. все его уровни заполнены, за исключением, возможно, последнего уровня, в котором
могут отсутствовать некоторые крайние справа листья.
2. Требование доминирования родительских узлов. Ключ в каждом узле не
меньше ключей в его дочерних узлах.
--
Последовательность значений на любом пути от корня к листу убывающая
(невозрастающая, если допускается наличие одинаковых ключей). Однако
упорядоченности ключей слева направо нет, т.е. нет никаких соотношений между
значениями ключей в узлах на одном уровне дерева или, в общем случае, в левом
и правом поддеревьях одного узла.
Свойства пирамиды:
1. Высота пирамиды равна `|__log2 n__|`.
2. Корень пирамиды всегда содержит её наибольший элемент.
3. Любой узел пирамиды со всеми его потомками также является пирамидой.
--
Пирамида может быть реализована в виде массива `H[1..n]` путем записи ее
элементов сверху вниз слева направо. Дочерние ключи по отношению к родительскому в позиции `i`
находятся в позициях `2i` и `2i + 1`; родительский ключ для ключа в позиции `i` в позиции `|__i//2__|`.
Для построения пирамиды можно добавлять элементы в ранее построенную пирамиду, применяя метод уменьшения размера задачи снизу вверх.
--
Добавим новый узел с ключом `K` после последнего листа имеющейся
пирамиды, а затем переместим `K` в соответствующее его значению место в
новой пирамиде следующим образом. Сравним `K` с родительским ключом: если
он не меньше `K`, алгоритм прекращает работу (полученная структура является
пирамидой). В противном случае обменяем эти два ключа и будем сравнивать `K`
с новым родителем. Этот процесс продолжается до тех пор, пока `K` не перестанет
превышать значение ключа в родительском узле или не достигнет корня.
Такая вставка не может требовать большего количества
сравнений ключей, чем высота пирамиды. Поскольку высота пирамиды с `n` узлами
`|__log2 n__|`, временная эффективность вставки составляет `O(log n)`.
--
Удаление корневого ключа из пирамиды можно выполнить при
помощи следующего алгоритма:
1. Обменять ключ в корне с последним ключом пирамиды.
2. Уменьшить размер пирамиды на 1.
3. "Пирамидизировать" уменьшенное дерево путем перемещения `K` вниз по
дереву.
Эффективность операции удаления определяется количеством выполняемых
сравнений ключей, необходимых для "пирамидизации" дерева. Поскольку не может
потребоваться сравнений больше, чем удвоенная высота пирамиды, временная
эффективность удаления из пирамиды — `O(log n)`.
--
*Пирамидальная сортировка* выполняется следующим образом:
1. Строим пирамиду для заданного массива.
2. Применяем операцию удаления корня `n-1` раз.
Так как элементы массива удаляются в порядке уменьшения и удаляемый элемент
располагается последним, массив, получающийся в результате пирамидальной
сортировки, оказывается отсортирован в порядке возрастания.
--
Выполним анализ количества сравнений ключей, необходимого
для удаления корневых ключей из пирамид уменьшающегося размера от `n` до 2:
`C(n) <= 2 sum_{i=1}^{n-1} log_2 i <= 2 sum_{i=1}^{n-1} log_2 (n-1) <= 2 n log_2 n in Theta(n log n)`.
Аналогичная оценка для первого шага алгоритма.
Подробный анализ показывает, что в временная эффективность пирамидальной сортировки равна
`Theta(n log n)` как в среднем, так и в наихудшем случаях, как у сортировки слиянием, но,
в отличие от последней, выполняется "на месте", без привлечения
дополнительной памяти.
