Подразделы

Другие разделы

Дата и время

04/04/2025 11:15:23

Авторизация

Метод декомпозиции

Идея метода декомпозиции Сортировка слиянием Быстрая сортировка Решение задач о паре ближайших точек и умножении в столбик

Решение задач о паре ближайших точек и умножении в столбик

Рассмотрим снова задачу поиска пары ближайших точек в множестве $S$ из $n$ точек. Предположим, что точки упорядочены в соответствии с возрастанием их координаты $x$ (если это не так, то их можно упорядочить за время $O(n log n)$ при помощи сортировки слиянием).

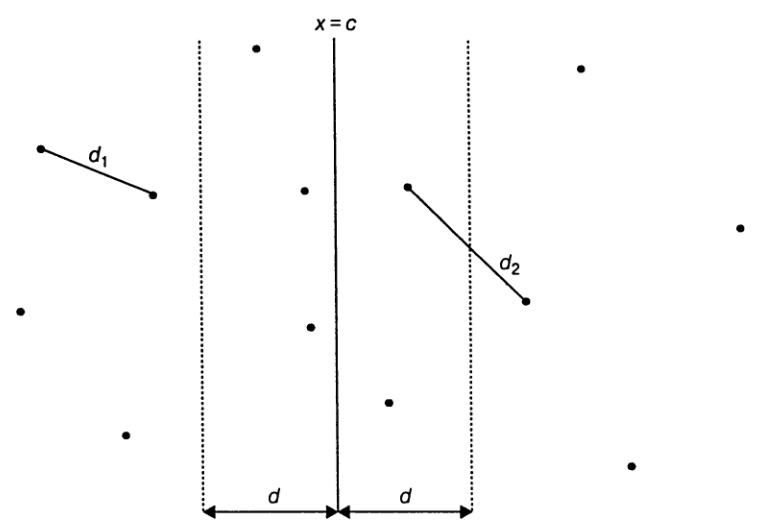
Используем метод декомпозиции и разделим множество на два подмножества $S_1$ и $S_2$ ( $S_1 uu S_2 = S$ ), состоящие из $n//2$ точек каждое, проведя вертикальную линию $x=c$ так, чтобы слева и справа от нее оказалось по $n//2$ точек.

Находим рекурсивно пары ближайших точек в левом подмножестве $S_1$ и в правом подмножестве $S_2$ . Пусть $d_1$ и $d_2$ – наименьшие расстояния между парами точек в подмножествах $S_1$ и $S_2$ , соответственно. Обозначим $d = min(d_1, d_2)$ . $d$ может не являться наименьшим расстоянием между парами точек в $S$ , поскольку точки с минимальным расстоянием между ними могут находиться в разных подмножествах.

Таким образом, этап комбинирования должен включать рассмотрение таких точек. Очевидно, что можно ограничиться рассмотрением точек, попадающих в вертикальную полосу шириной $2d$ , поскольку расстояние между любыми другими парами точек по разные стороны от разделяющей линии заведомо превосходит расстояние $d$ . Пусть $C_1$ и $C_2$ — подмножества таких точек в левой и правой части полосы, соответственно.

width:400px|Поиск

Теперь для каждой точки $P(x, y)$ из $C_1$ мы должны рассмотреть точки в $C_2$ , которые могут оказаться от точки $P$ на расстоянии, меньшем $d$ . Совершенно очевидно, что координаты $y$ таких точек не могут выходить за пределы интервала $[y-d, y + d]$ . Таких точек может быть не более шести, поскольку любая пара точек в $C_i$ находится как минимум на расстоянии $d$ друг от друга.

Если списки точек в $C_1$ и $C_2$ будут отсортированы в порядке возрастания их координат $y$ , то можно рассматривать точки $C_1$ по порядку, в то время как указатель в списке $C_2$ будет двигаться в пределах отрезка $2d$ , выбирая до шести кандидатов, для которых будут вычисляться расстояния до текущей точки $P$ из списка $C_1$ . Можно оценить количество операций $f(n)$ , необходимое для комбинирования решений меньших подзадач, как $O(n)$ .

Если рекурсивный вызов будет возвращать не только минимальное расстояние, но и отсортированное в порядке возрастания $y$ множество, тогда из отсортированных $S_1$ и $S_2$ мы сможем получить отсортированное $S$ с помощью алгоритма Merge за $O(n)$ .

Получить $C_1$ из $S_1$ и $C_2$ из $S_2$ можно с помощью фильтрации тоже за $O(n)$ .

В результате рекуррентное соотношение для времени работы $T(n)$ описанного алгоритма над $n$ предварительно отсортированными точками имеет вид:
$T(n) = 2 T(n/2) + O(n)$ .

Применяя основную теорему для $a=2$ , $b=2$ и $d=1$ , получаем, что $Т(n) in O(n log n)$ .

Предварительная сортировка точек по координате $x$ не меняет класс эффективности алгоритма, так как имеет такой же класс $O(n log n)$ .

Если мы используем классический алгоритм умножения двух $n$ -значных чисел в столбик, то каждая из $n$ цифр одного числа будет умножаться на каждую из $n$ цифр второго числа, что в результате дает нам $n^2$ умножений цифр. Если у одного числа количество цифр меньше, чем у второго, впереди к нему можно дописать некоторое количество нулей, чтобы длина чисел стала одинаковой.

Для любой пары двузначных чисел $a = a_1*10+a_0$ и $b =b_1*10+ b_0$ их произведение можно вычислить по формуле
$c=a*b=(a_1*10+a_0)*(b_1*10+ b_0)=$
$=a_1*b_1*100+(a_1*b_0+a_0*b_1)*10+a_0*b_0=c_2*100+c_1*10+c_0$
Здесь 4 умножения, но количество умножений можно уменьшить, если вычислять $c_1$ другим способом:
$c_1=(a_1+a_0)*(b_1+b_0)-(c_2+c_0)$ .

Теперь применим этот трюк к произведению двух $n$ -значных чисел $a$ и $b$ , где $n$ - положительное четное число. Разделим числа пополам, тогда $a = a_1*10^{n//2}+a_0$ и $b =b_1*10^{n//2} + b_0$ , а для произведения получим
$c=a*b=(a_1*10^{n//2}+a_0)*(b_1*10^{n//2}+ b_0)=$
$=a_1*b_1*10^n+(a_1*b_0+a_0*b_1)*10^{n//2}+a_0*b_0=c_2*10^n+c_1*10^{n//2}+c_0$
где $c_1=(a_1+a_0)*(b_1+b_0)-(c_2+c_0)$ .

Поскольку перемножение n-значных чисел требует трех умножений
$n//2$ -значных чисел, рекуррентное соотношение для количества умножений $M(n)$ имеет вид
$M(n) = 3*M(n//2)$ при $n> 1$ , $M(1) = 1$ .

Решение этого уравнения методом обратной подстановки для $n = 2^k$ дает
$M(2^k) = 3^k$

Поскольку $k = log_2 n$ ,
$M(n) = 3^{log_2 n} = n^{log_2 3} ~~ n^{1.585}$ .

В экспериментах алгоритм декомпозиции превосходил метод умножения в столбик только для чисел длиной более 600 цифр.

Задания для практики

а) Напишите псевдокод декомпозиционного алгоритма для поиска позиции наибольшего элемента в массиве из $n$ чисел.
б) Какими будут выходные данные алгоритма, если наибольшее значение имеют несколько элементов?
в) Напишите и решите рекуррентное соотношение для количества сравнений ключей, выполняемых алгоритмом.
г) Сравните созданный вами алгоритм с алгоритмом для решения указанной задачи, основанным на грубой силе.
а) Напишите псевдокод декомпозиционного алгоритма для вычисления $а^n$ , где $а > 0$ , а $n$ — натуральное число.
б) Напишите и решите (для $n=2^k$ ) рекуррентное соотношение для количества умножений, выполняемых алгоритмом.
в) Сравните созданный вами алгоритм с алгоритмом для решения указанной задачи, основанным на грубой силе.
Разработайте на основе метода декомпозиции алгоритм решения одномерной версии задачи о паре ближайших точек, т.е. задачи поиска пары ближайших чисел во множестве из п действительных чисел. Определите класс эффективности предложенного вами алгоритма.
Разработайте на основе метода декомпозиции алгоритм решения задачи о паре ближайших точек в пространстве (3d). Определите класс эффективности предложенного вами алгоритма.