Подразделы

Другие разделы

Дата и время

09/04/2025 21:48:44

Авторизация

Метод декомпозиции

Идея метода декомпозиции Сортировка слиянием Быстрая сортировка Решение задач о паре ближайших точек и умножении в столбик

Сортировка слиянием

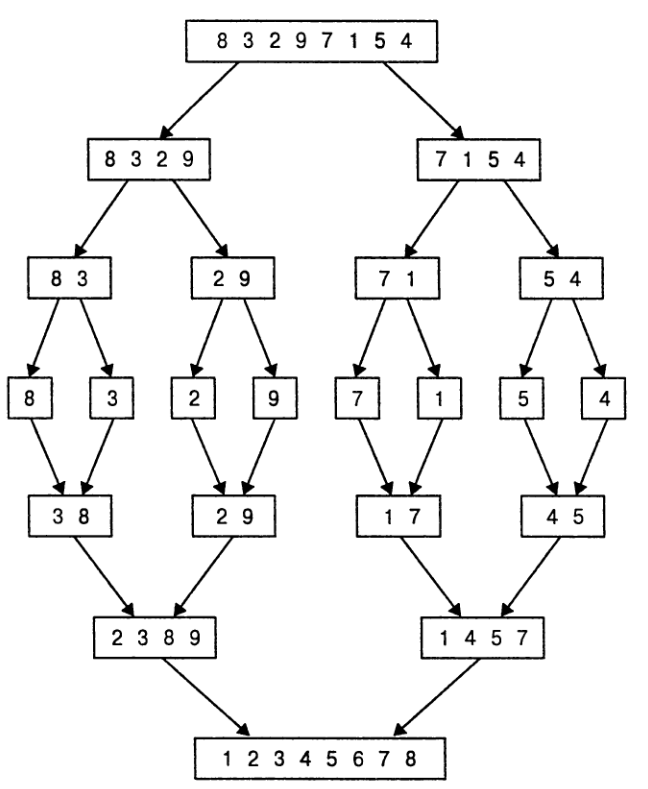
Сортировка слиянием является примером успешного применения метода декомпозиции. Она сортирует заданный массив $A[0...n-1]$ путем разделения его на две половины, рекурсивной сортировки каждой половины и слияния двух отсортированных половин в один отсортированный массив.

Алгоритм MergeSort $(A,l,r)$
// Входные данные: Подмассив $A[l...r]$ массива $A[0...n - 1]$ ,
// определяемый начальным и конечным индексами $l$ и $r$
// Выходные данные: Подмассив $A[l...r]$ , отсортированный
// в неубывающем порядке
if $l<r$
$quad m larr |__(l+r)//2__|$
$quad$ Mergesort $(A,l,m)$
$quad$ Mergesort $(A,m+1,r)$
$quad$ Merge $(A,l,m,r)$

Слияние двух отсортированных массивов можно выполнить следующим образом. Два указателя (индекса массивов) после инициализации указывают на первые элементы сливаемых массивов. Затем элементы, на которые указывают указатели, сравниваются, и меньший из них добавляется в новый массив. После этого индекс меньшего элемента увеличивается, и он указывает на элемент, непосредственно следующий за только что скопированным. Эта операция повторяется до тех пор, пока не будет исчерпан один из сливаемых массивов, после чего оставшиеся элементы второго массива просто добавляются в конец нового массива.

Алгоритм Merge $(A,l,m,r)$
// Входные данные: Сортированные подмассивы $A[l...m]$ и $A[m+1...r]$
// Выходные данные: Сортированный подмассив $A[l...r]$ ,
$p larr m-l+1; q larr r-m; i larr 0; j larr 0; k larr l$
Копировать $A[l...m]$ в массив $B[0...p-1]$
Копировать $A[m+1...r]$ в массив $C[0...q-1]$
while $i < p$ and $j < q$ do
$quad$ if $B[i] <= C[j]$
$quad quad A[k] larr B[i]; i larr i + 1$
$quad$ else
$quad quad A[k] larr C[j]; j larr j + 1$
$quad k larr k+1$
if $i < p$
$quad$ Копировать $B[i...p-1]$ в массив $A[k...r]$
else
$quad$ Копировать $C[j...q-1]$ в массив $A[k...r]$

width:300px|Сортировка

Основной операцией при слиянии является операция сравнения (операция присваивания для любых алгоритмов сортировки считается менее важной).

На каждом шаге выполняется в точности одно сравнение, после которого общее количество элементов в двух сливаемых массивах уменьшается на 1. В худшем случае ни один из массивов не исчерпывается до самого конца, пока в другом массиве не останется только один элемент. Следовательно, в наихудшем случае
$C_{"merge"}(n) =n-1$ ,
и мы получаем рекуррентное соотношение для количества сравнений:
$C_{"worst"} (n) = 2 C_{"worst"}(n//2) + n-1$ для $n > 1$ , $C_{"worst"} (1) = 0$ .

Согласно основной теореме, $C_{"worst"} (n) in Theta (n log n)$

Точное решение для $n=2^k$ : $C_{"worst"} (n)=n log_2 n -n+1$

Количество сравнений ключей, выполняемых сортировкой слиянием, в худшем случае весьма близко к теоретическому минимуму количества сравнений для любого алгоритма сортировки, основанного на сравнениях
$|~log_2 n!~| ~~ |~ n log_2 n - 1.44n ~|$ .