Подразделы

Другие разделы

Дата и время

09/04/2025 21:48:44

Авторизация

Метод декомпозиции

Идея метода декомпозиции Сортировка слиянием Быстрая сортировка Решение задач о паре ближайших точек и умножении в столбик

Быстрая сортировка

В отличие от сортировки слиянием, которая разделяет элементы массива в соответствии с их положением в массиве, быстрая сортировка разделяет элементы массива в соответствии с их значениями. Конкретно она выполняет перестановку элементов данного массива $А[0..n - 1]$ для получения разбиения, когда все элементы до некоторой позиции $s$ не превышают элемента $A[s]$ , а элементы после позиции $s$ не меньше $A[s]$ :

$ubrace(A_0, ..., A_{s-1})_("элементы "<=A_s), A_s, ubrace(A_{s+1}, ..., A_{n-1})_("элементы ">=A_s)$

Очевидно, что после разбиения $A[s]$ находится в окончательной позиции в отсортированном массиве, и мы можем сортировать два подмассива элементов до и после $A[s]$ независимо (например, тем же самым методом).

Алгоритм QuickSort $(A, l, r)$
// Входные данные: Подмассив $A[l...r]$ массива $A[0...n - 1]$ ,
// определяемый начальным и конечным индексами $l$ и $r$
// Выходные данные: Подмассив $A[l...r]$ , отсортированный
// в неубывающем порядке
if $l < r$
$quad s larr "Partition"(A,l,r)$ // $s$ — позиция разбиения
$quad$ Quicksort $(A,l,s-1)$
$quad$ Quicksort $(A,s+1,r)$

Разбиение массива $A[0...n - 1]$ и, в общем случае, его подмассива $A[l...r]$ ( $0 <= l < n <= n - 1$ ) можно выполнить следующим образом. Сначала выбирается элемент, относительно которого будет выполняться разбиение, он называется опорным. Имеется ряд стратегий для выбора опорного элемента, в простейшем случае можно выбрать первый элемент подмассива: $p = A[l]$ .

Для разбиения будем использовать метод, основанный на использовании двух указателей (индексах массива). Левый индекс $i$ сначала устанавливается на второй элемент. Поскольку мы хотим, чтобы элементы, меньшие опорного, находились в первой части подмассива, мы пропускаем элементы, меньшие опорного, и останавливамся, встретив первый элемент, который не меньше опорного. Правый индекс $j$ сначала устанавливается на последний элемент подмассива. Поскольку надо, чтобы все элементы, большие опорного, находились во второй части подмассива, мы пропускаем все элементы, большие опорного, и останавливаемся, встретив первый элемент, не превышающий опорный.

Возможны три ситуации для индексов $i$ и $j$ в момент остановки. Если $i < j$ , то мы просто обмениваем элементы $A[i]$ и $A[j]$ и продолжаем сканирование массива:

width:400px|Сортировка

Если $i > j$ , то мы завершаем разбиение, обменивая опорный элемент $A[l]$ с $A[j]$ и возвращая $j$ в качестве результата функции:

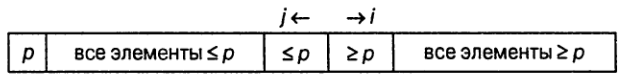
width:400px|Сортировка

Если индексы остановились на одном элементе ( $i=j$ ), то значение этого элемента должно быть равно $p$ .

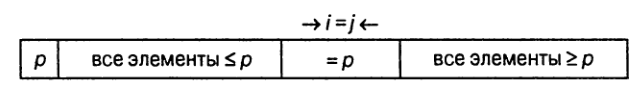
width:400px|Сортировка

Можно поступить так же, как в предыдущем случае.

Алгоритм Partition $(A,l,r)$
// Входные данные: Подмассив $A[l...r]$ массива $A[0...n - 1]$ ,
// определяемый начальным и конечным индексами $l$ и $r$
// Выходные данные: разбиение $A[l...r]$ , возвращается позиция разбиения
$p larr A[l]; i larr l+1; j larr r$
repeat
$quad$ while $A[i]<p$ do
$quad quad quad i larr i+1$
$quad$ while $A[j]>p$ do
$quad quad quad j larr j-1$
$quad$ if $i>=j$
$quad quad quad$ обмен $A[l]$ и $A[j]$
$quad quad quad$ return $j$
$quad$ обмен $A[i]$ и $A[j]$
$quad i larr i+1; j larr j-1$

Возможен выход индекса $i$ за пределы границ подмассива, нужно добавить проверку $i<=r$ .

Количество сравнений ключей, выполненных при разбиение, достигает величины $n+1$ , если $i>j$ .

Если все разбиения оказываются посредине соответствующих подмассивов, реализуется наилучший случай. Тогда количество сравнений вычисляется из рекуррентного соотношения
$C_{"best"}(n)=2 C_{"best"}(n//2) + n$ при $n > 1$ , $C_{"best"}(1) = 0$ .

Согласно основной теореме, $C_{"best"}(n) in Theta (n log_2 n)$ .

В наихудшем случае все разбиения оказываются такими, что один из подмассивов пуст, а размер второго на 1 меньше размера разбиваемого массива. Такая ситуация возникает, в частности, в возрастающем массиве, т.е. для входных данных, для которых задача сортировки уже решена!

После выполнения $n + 1$ сравнений, выясняется, что теперь следует сортировать строго возрастающий массив $A[1... n-1]$ .

Общее количество выполненных сравнений составляет
$C_{"worst"}(n)=n+1+n+...+3=(n+4)*(n-1)//2 in Theta(n^2)$ .

Таким образом, встает вопрос об эффективности алгоритма в среднем случае. Считая, что разбиение может выполняться в каждой позиции $s$ ( $0 <= s < n-1$ ) с одинаковой вероятностью $1//n$ , получаем следующую оценку:
$C_{"avg"}(n) ~~ 2 n ln n ~~ 1.38 n log_2 n$ .

Таким образом, алгоритм быстрой сортировки в среднем случае выполняет сравнений ключей всего на 38% больше, чем в наилучшем случае. Кроме того, внутренний цикл данного алгоритма настолько эффективен, что для случайных массивов он работает быстрее, чем сортировка слиянием.

Исследователями были предложены улучшенные методы выбора опорного элемента (например, разбиение на основе медианы трех элементов, когда в качестве опорного элемента используется медиана крайнего слева, справа и среднего элементов массива), переключение на сортировку вставками для малых подмассивов.

Назад

Подразделы

Другие разделы

Дата и время

Авторизация

Метод декомпозиции

Быстрая сортировка