Подразделы

Другие разделы

Дата и время

09/04/2025 21:48:44

Авторизация

Метод декомпозиции

Идея метода декомпозиции Сортировка слиянием Быстрая сортировка Решение задач о паре ближайших точек и умножении в столбик

Идея метода декомпозиции

Метод декомпозиции (он же метод "разделяй и властвуй") является, вероятно, наиболее популярным методом разработки алгоритмов. Ряд очень эффективных алгоритмов представляют собой реализации этой общей стратегии. Алгоритмы, основанные на методе декомпозиции, работают в соответствии со следующим планом.

Экземпляр задачи разбивается на несколько меньших экземпляров той же задачи, в идеале – одинакового размера.
Решаются меньшие экземпляры задачи (обычно рекурсивно, хотя иногда для небольших экземпляров применяется какой-нибудь другой алгоритм).
При необходимости решение исходной задачи находится путем комбинации решений меньших экземпляров.

Анализ метода декомпозиции

В качестве примера рассмотрим задачу вычисления суммы чисел $a_0,..., a_{n-1}$ . Если $n > 1$ , задачу можно разделить на два экземпляра той же задачи: вычисление суммы первых $|__ n//2 __|$ чисел и вычисление суммы оставшихся $|~ n//2 ~|$ чисел. При $n = 1$ в качестве ответа просто возвращается значение $a_0$ . Как только каждая из этих двух сумм будет вычислена (с применением описанного метода, т.е. рекурсивно), мы сможем сложить их значения, чтобы получить окончательный ответ.

Этот алгоритм не является более эффективным способом суммирования $n$ чисел по сравнению с алгоритмом на основе грубой силы, так как количество операций сложения не изменилось. Но каждая подзадача может быть решена отдельным процессором, поэтому метод декомпозиции является основным при разработке параллельных алгоритмов.

В общем случае задача размера $n$ может быть разделен на несколько подзадач размером $n/b$ , из которых требуется решить $a$ подзадач ( $а >= 1, b > 1$ ). Для упрощения анализа будем считать, что $n=b^k$ . Получаем следующее рекуррентное соотношение для времени работы алгоритма, которое называется обобщенным рекуррентным уравнением декомпозиции:
$T(n) = a T(n/b) + f(n)$ ,
где $f(n)$ – функция, учитывающая затраты времени на разделение задачи на меньшие подзадачи и комбинирование решений подзадач.

В примере с суммированием чисел $a=b=2$ и $f(n) =1$ .

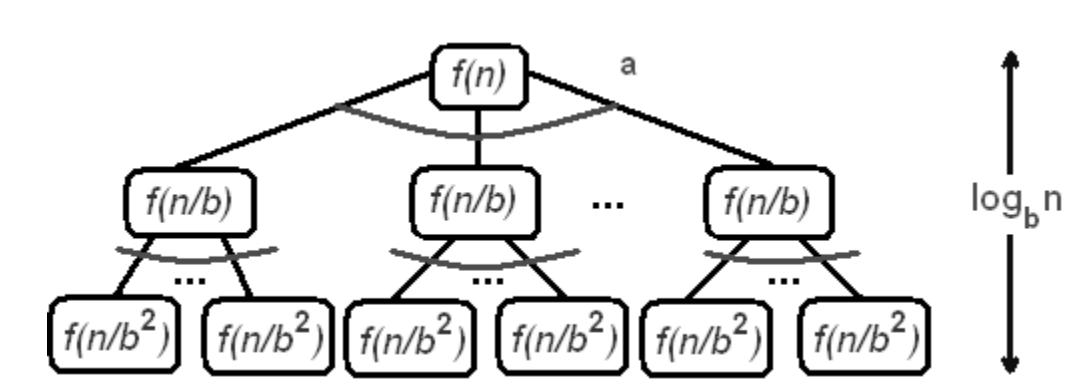
width:350px|Дерево

Дерево содержит $a^{log_b n}=n^{log_b a}$ листьев.

Основная теорема

Если в рекуррентном уравнении $f(n) in Theta(n^d)$ , где $d >= 0$ , то $T(n) in { (Theta(n^d)," если ",a<b^d),(Theta(n^d log n)," если ",a=b^d),(Theta(n^{log_b a})," если ",a>b^d) :}$

В примере с суммированием чисел $a=b=2$ и $f(n)=1=n^0$
$T(n)=Theta(n^{log_2 2})=Theta(n)$ , так как $a>b^0$ .

Таким образом мы можем указать класс эффективности алгоритма, не решая само рекуррентное уравнение.