Подразделы
Другие разделы
| Занятие 1 |
| Занятие 2 |
| Занятие 3 |
| Занятие 4 |
| Занятие 5 |
| Занятие 6 |
| Занятие 7 |
| Занятие 8 |
| Занятие 9 |
| Занятие 10 |
| Занятие 11 |
| Занятие 12 |
| Занятие 13 |
| Занятие 15 |
| Занятие 16 |
| Занятие 17 |
| Занятие 18 |
| Занятие 19 |
| Занятие 20 |
Дата и время
26/02/2026 10:02:12
 Занятие 14
Занятие 14
Классификация игр Минимаксный алгоритм, альфа-бета отсечение Игра ним и другие Ним-значение и теория Гранди
 Минимаксный алгоритм, альфа-бета отсечение
Минимаксный алгоритм, альфа-бета отсечение
Наиболее универсальным методом для решения задач на антагонистические игры является построение дерева игры, вершинами в которой служат позиции, возникающие в игре. Потомками в дереве являются те позиции, которые можно получить из родительской позиции. Листьями этого дерева являются финальные позиции игры. Если в финальной позиции выигрывает первый участник игры, то она получает оценку +1, если второй, то –1, если ничья, то 0. В играх, где сумма выигрыша может быть различной, в качестве оценки позиции можно использовать сумму выигрыша.
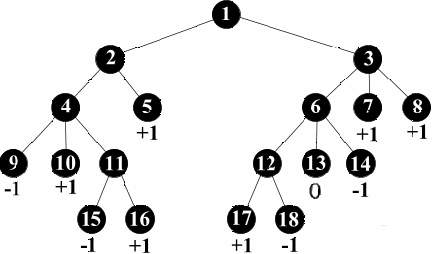
Для нахождения оценки начальной позиции используется минимаксный алгоритм. Оценка позиции, в которой ход делает первый участник, вычисляется как максимум из оценок позиций-потомков. Оценка позиции, в которой ход делает второй участник, вычисляется как минимум из оценок позиций-потомков. Первого участника часто называют Макс, а второго – Мин. Для начальной позиции на рисунке получается оценка +1. Выигрышным является любой ход из начальной позиции, приводящий к позиции с максимальной оценкой.
В сложных играх полный анализ дерева игры слишком трудоемок. Для решения этой проблемы можно использовать следующие способы.
- Можно не доводить построение дерева игры по финальных позиций, а использовать эвристические оценки текущей позиции. Позиция, в которой первый игрок имеет некоторое позиционное преимущество, получает положительное значение, и наоборот. Например, позиция в шахматах, в которой у первого игрока на 2 пешки больше, может получить оценку +0,1.
- Одинаковые позиции могут встречаться на разных ветках дерева игры. Можно повторно не вычислять их оценку, а использовать уже ранее вычисленную. Для этого необходимо сохранять вычисленные оценки в таблице вида [позиция,оценка].
- Можно не анализировать позиции, которые ведут к ухудшению предварительной оценки, полученной при анализе других возможных ходов. Для этого задают интервал `[α,β]`, где `α` – минимум оценки позиции, на который может надеяться Макс, `β` – максимум, на который может надеяться Мин. Если текущая оценка позиции выйдет за границы интервала, то остальные возможные ходы из этой позиции не рассматриваются, так как дальнейший анализ может только еще больше изменить оценку, а у Макса или Мина уже есть ход с лучшей оценкой. Сначала интервал `[α,β]` равен `(-∞,+∞)`, по мере вычислений его границы изменяются. Граница `α` меняется при вычислении оценки позиций Макса, а граница `β` – при вычислении оценки позиций Мина.
Этим способом можно решить, например, следующие задачи.
В некоторых играх можно обойтись без построения дерева игры, используя жадную стратегию, симметричную стратегию или шахматную раскраску поля. Примеры задач:
- Игра с карточками
- Игра в точки
- Игра в куриные яйца. Игроков — двое, и они по очереди выкладывают яйца одинакового размера на квадратную салфетку. После того, как яйцо положено на стол, его нельзя ни передвигать, ни касаться другим яйцом. Так продолжается до тех пор, пока салфетка не будет столь густо покрыта яйцами, что свободного места для очередного яйца уже не останется. Игрок, положивший яйцо последним, объявляется победителем. Если тот, кто начинает игру, выберет правильную стратегию, он обязательно выиграет. «Проще простого, если вы знаете, в чем тут дело», — так говорил великий мореплаватель. По преданию начинавший игру первым Колумб стукнул яйцом по столу, слегка надломил скорлупу и поставил яйцо вертикально в центр платка. Что бы ни делал в дальнейшем противник, нужно повторять его ходы, кладя очередное яйцо с противоположной стороны первого яйца. Первое яйцо играет здесь роль центра симметрии, поэтому место для нового яйца обязательно отыщется. А противник в конце концов «задохнется».
- Игра Так-тикс. На доске `n`x`n` расставлены одинаковые фишки, на каждом поле по одной. Игроки по очереди берут несколько фишек из одного вертикального или горизонтального ряда, причем обязательно подряд. Выигрывает тот, кто берет последнюю фишку. Используя симметричную стратегию, первый игрок выигрывает на досках нечетного размера, а второй на досках четного размера. Интересно, что для мизерного варианта этой игры (взявший последнюю фишку проигрывает) нет такой простой стратегии и требуется полный анализ дерева игры.

 Начало
Начало