Подразделы
Другие разделы
| Занятие 1 |
| Занятие 2 |
| Занятие 3 |
| Занятие 4 |
| Занятие 5 |
| Занятие 6 |
| Занятие 7 |
| Занятие 8 |
| Занятие 9 |
| Занятие 10 |
| Занятие 11 |
| Занятие 12 |
| Занятие 14 |
| Занятие 15 |
| Занятие 16 |
| Занятие 17 |
| Занятие 18 |
| Занятие 19 |
| Занятие 20 |
Дата и время
05/01/2026 07:32:24
 Занятие 13
Занятие 13
A. ASCII Art B. Billing Tables C. Cellular Automaton D. Driving Directions E. Exchange F. Fool's Game G. Graveyard H. Hard Life I. Interconnect J. Java vs C++ K. Kickdown
 H. Hard Life
H. Hard Life
 Олимпиадные задачи на английском языке
Олимпиадные задачи на английском языке
| 12/12/2006 | Практическое занятие 13 (задачи NEERC 2006) (H) |
Ограничения: время – 3s/6s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
John is a Chief Executive Officer at a privately owned medium size company. The owner of the company
has decided to make his son Scott a manager in the company. John fears that the owner will ultimately
give CEO position to Scott if he does well on his new manager position, so he decided to make Scott’s
life as hard as possible by carefully selecting the team he is going to manage in the company.
John knows which pairs of his people work poorly in the same team. John introduced a hardness factor
of a team — it is a number of pairs of people from this team who work poorly in the same team divided
by the total number of people in the team. The larger is the hardness factor, the harder is this team to
manage. John wants to find a group of people in the company that are harderst to manage and make it
Scott’s team. Please, help him.
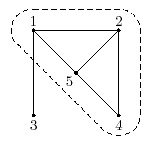
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5
pairs work poorly in the same team, thus hardness factor is equal to 5/4 . If we add person number 3 to
the team then hardness factor decreases to 6/5.
Input
The first line of the input file contains two integer numbers `n` and `m\ (1\ ≤\ n\ ≤\ 100,\ 0\ ≤\ m\ ≤\ 1000)`. Here
`n` is a total number of people in the company (people are numbered from 1 to `n`), and `m` is the number
of pairs of people who work poorly in the same team. Next `m` lines describe those pairs with two integer
numbers `a_i` and `b_i\ (1\ ≤\ a_i;\ b_i\ ≤\ n,\ a_i\ ≠\ b_i)` on a line. The order of people in a pair is arbitrary and no
pair is listed twice.
Output
Write to the output file an integer number `k\ (1\ ≤\ k\ ≤\ n)` — the number of people in the hardest team,
followed by `k` lines listing people from this team in ascending order. If there are multiple teams with the
same hardness factor then write any one.
Sample Input #1
5 6 1 5 5 4 4 2 2 5 1 2 3 1
Sample Output #1
4 1 2 4 5
Sample Input #2
4 0
Sample Output #2
1 1
Note, that in the last example any team has hardness factor of zero, and any non-empty list of people is
a valid answer.
Source: NEERC ICPC, 2006
 Начало
Начало