Подразделы
Другие разделы
| Занятие 1 |
| Занятие 2 |
| Занятие 3 |
| Занятие 4 |
| Занятие 5 |
| Занятие 6 |
| Занятие 7 |
| Занятие 8 |
| Занятие 9 |
| Занятие 10 |
| Занятие 11 |
| Занятие 12 |
| Занятие 14 |
| Занятие 15 |
| Занятие 16 |
| Занятие 17 |
| Занятие 18 |
| Занятие 19 |
| Занятие 20 |
Дата и время
05/01/2026 07:08:18
 Занятие 13
Занятие 13
A. ASCII Art B. Billing Tables C. Cellular Automaton D. Driving Directions E. Exchange F. Fool's Game G. Graveyard H. Hard Life I. Interconnect J. Java vs C++ K. Kickdown
 C. Cellular Automaton
C. Cellular Automaton
 Производящие функции и матричное представление
Производящие функции и матричное представлениеМатрицы
Олимпиадные задачи на английском языке

| 12/12/2006 | Практическое занятие 13 (задачи NEERC 2006) (C) |
Ограничения: время – 3s/6s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number
of discrete time steps according to a set of rules that describe the new state of a cell based on the states
of neighboring cells. The order of the cellular automaton is the number of cells it contains. Cells of the
automaton of order n are numbered from 1 to `n`.
The order of the cell is the number of different values it may contain. Usually, values of a cell of order
m are considered to be integer numbers from 0 to `m` – 1.
One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed.
In this problem we examine the special kind of cellular automaton — circular cellular automaton of order
`n` with cells of order `m`. We will denote such kind of cellular automaton as `n,m`-automaton.
A distance between cells `i` and `j` in `n,m`-automaton is defined as `min(|i-j|;\ n-|i-j|)`. A `d`-environment
of a cell is the set of cells at a distance not greater than `d`.
On each `d`-step values of all cells are simultaneously replaced by new values. The new value of cell `i` after
`d`-step is computed as a sum of values of cells belonging to the `d`-enviroment of the cell `i` modulo `m`.
The following picture shows 1-step of the 5,3-automaton.
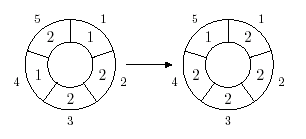
The problem is to calculate the state of the `n,m`-automaton after `k\ d`-steps.
Input
The first line of the input file contains four integer numbers `n,\ m,\ d,` and `k\ (1\ ≤\ n\ ≤\ 500,\ 1\ ≤\ m\ ≤\ 1\ 000\ 000,\ 0\ ≤\ d\ <\ n/2\ ,\ 1\ ≤\ k\ ≤\ 10\ 000\ 000)`. The second line contains `n` integer numbers
from 0 to `m` – 1 — initial values of the automaton’s cells.
Output
Output the values of the `n,m`-automaton’s cells after `k\ d`-steps.
Sample Input #1
5 3 1 1 1 2 2 1 2
Sample Output #1
2 2 2 2 1
Sample Input #2
5 3 1 10 1 2 2 1 2
Sample Output #2
2 0 0 2 2

 Начало
Начало