 Полиномы
Полиномы
 Быстрое умножение полиномов
Быстрое умножение полиномов
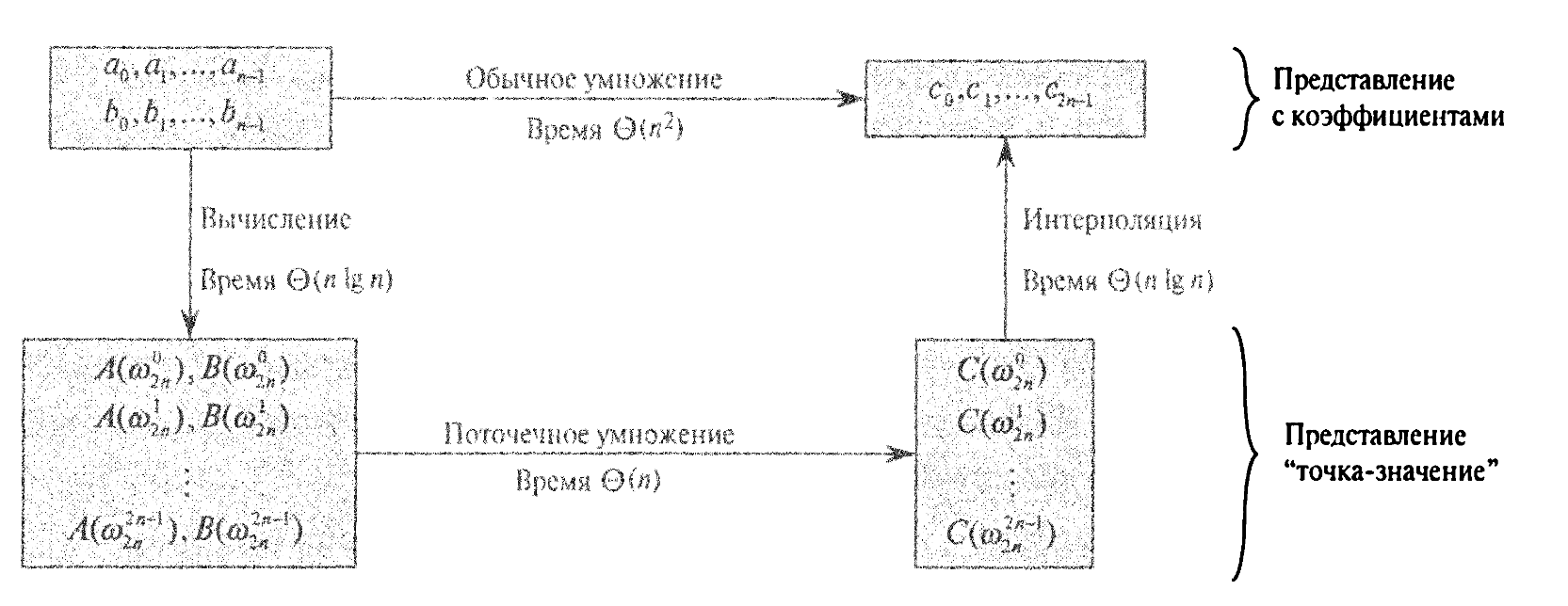
время выполнения которого линейно зависит от `n`, для ускорения
умножения полиномов, заданных в коэффициентной форме? Ответ зависит от способности
быстро выполнять преобразование полинома из коэффициентной формы
в форму пар точки-значения (вычисление) и обратно (интерполяция).
При правильном выборе точек `x_k` можно выполнять переход от одного представления к другому за время `Theta(n log n)`.
--
--
Если в качестве точек `x_k` выбрать комплексные корни из единицы, то представление
точки-значения можно получить с помощью дискретного преобразования Фурье
(DFT) вектора коэффициентов. Интерполяцию, можно выполнить путем применения обратного дискретного
преобразования Фурье к парам точки-значения, в результате чего получается вектор коэффициентов.
Можно предложить следующую основанную на БПФ процедуру умножения
двух полиномов `A(x)` и `B(x)` степени `n-1`, в которой исходные полиномы
и результат представлены в коэффициентной форме, а время выполнения
составляет `O(n log n)`. Предполагается, что `n+1=2^m`; это требование всегда
можно удовлетворить, добавив равные нулю старшие коэффициенты.
--
1. Удвоение степени. Создаются коэффициентные представления
полиномов `A(x)` и `В(x)` в виде полиномов степени `2n-1` путем
добавления `n` нулевых старших коэффициентов.
2. Вычисление. Определяются представления полиномов `A(х)` и `В(х)` в форме
набора пар точки-значения длины `2n` путем двукратного применения БПФ.
Эти представления содержат значения двух заданных полиномов в точках,
являющихся комплексными корнями степени `2n` из единицы.
--
3. Поточечное умножение. Вычисляется представление точки-значения
полинома `C(x) = A(x)*B(x)` путем поточечного умножения соответствующих
значений.
4. Интерполяция. Создается коэффициентное представление полинома `C(x)`
с помощью однократного применения БПФ к `2n` парам точка-значение для
вычисления обратного DFT.
--
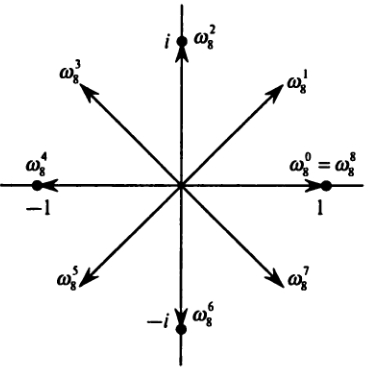 *Комплексным корнем n-й степени из единицы*
является комплексное число `omega`, такое что `omega^n = 1`.
Существует ровно `n` комплексных корней `n`-й степени из единицы: `е^{2 pi i k//n}= cos(2 pi k//n) + i*sin (2 pi k//n)`.
Значение `omega_n=е^{2 pi i//n}` называется главным значением корня `n`-й степени из единицы; все остальные комплексные корни `n`-й степени
из единицы являются его степенями: `omega_n^0, omega_n^1, ..., omega_n^{n-1}`.
--
Мы хотим вычислить полином
`P(x)=sum_{j=0}^{n-1} a_j*x^j`
в точках `omega_n^0, omega_n^1, ..., omega_n^{n-1}`:
`y_k=P(omega_n^k)=sum_{j=0}^{n-1} a_j*omega_n^{kj}`
`y = DFT_n (a)`
В методе БПФ применяется стратегия декомпозиции, в которой отдельно
используются коэффициенты полинома `P(х)` с четными и нечетными индексами:
`P'(x) =a_{n-2} x^{n//2-1}+a_{n-4} x^{n//2-2}+...+ a_2 x+a_0`
`P''(x) =a_{n-1} x^{n//2-1}+a_{n-3} x^{n//2-2}+...+ a_3 x+a_1`
--
Для определенных таким способом полиномов справедливо равенство `P(x)=P'(x^2)+x*P''(x^2)`
Задача вычисления полинома `P(x)` в точках `omega_n^0, omega_n^1, ..., omega_n^{n-1}` сводится
к вычислению двух полиномов `P'(x)` и `P''(x)` степени `n//2-1` в точках `(omega_n^0)^2, (omega_n^1)^2, ..., (omega_n^{n-1})^2`
а затем объединению результатов с использованием формулы.
Каждый корень встречается в списке `(omega_n^0)^2, (omega_n^1)^2, ..., (omega_n^{n-1})^2` ровно два раза, так как существует только `n//2` комплексных корней степени `n//2` из единицы.
--
Следовательно, полиномы `P'(x)` и `P''(x)` с границей степени `n//2` рекурсивно вычисляются в `n//2` комплексных корнях `n//2`-й степени из единицы.
Эти подзадачи имеют точно такой же вид, как и исходная задача, но их размерность вдвое меньше. Таким образом, мы свели
вычисление `n`-элементного `DFT_n` к вычислению двух `n//2`-элементных `DFT_{n//2}`.
--
```c++
void dft(vector<complex<double>>& a) {
int n = a.size();
if (n == 1) return;
int n2=n/2;
vector<complex<double>> a1(n2), a2(n2);
for (int i=0, j=0; i<n; i+=2, ++j) {
a1[j] = a[i];
a2[j] = a[i+1];
}
dft(a1); dft(a2);
double ang = 2.0*acos(-1.0)/n;
complex<double> w(1), wn(cos(ang), sin(ang));
for (int i=0; i<n2; ++i) {
a[i] = a1[i] + w*a2[i];
a[i+n2] = a1[i] - w*a2[i];
w *= wn;
}
}
```
--
Обратное дискретное преобразование Фурье `DFT_n^{-1}(у)` вычисляется по формуле:
`a_j=1/n * sum_{k=0}^{n-1} y_k*omega_n^{-kj}`
Сравнивая уравнения, мы видим, что если модифицировать алгоритм БПФ --
поменять ролями `a` и `y`, заменить `omega_n` на `omega_n^{-1}` и разделить каждый элемент результата на `n` -
получится обратное DFT. Таким образом, `DFT_n` также можно вычислить за время `O(n log n)`.
`c=DFT_{2n}^{-1} (DFT_{2n}(a) * DFT_{2n} (b))`
--
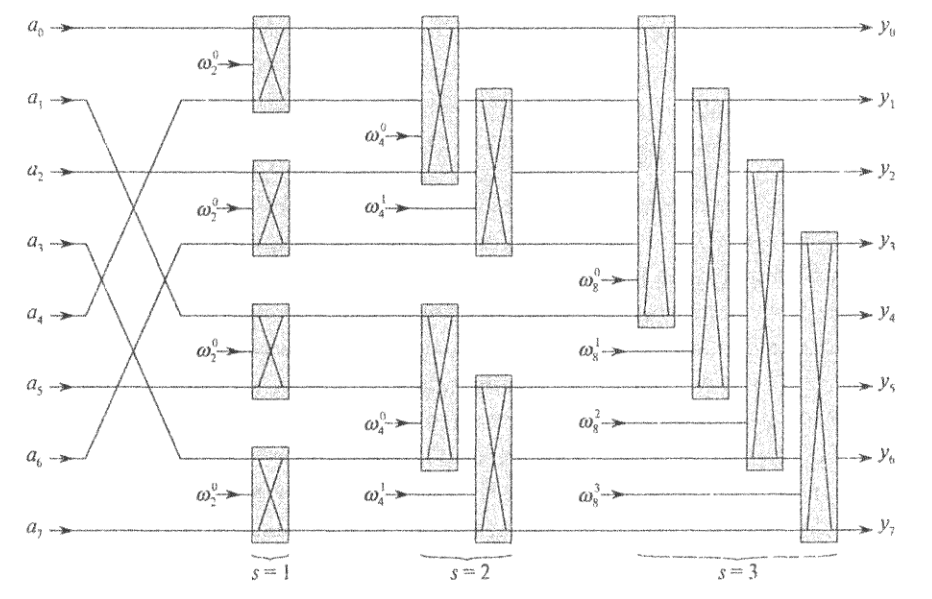
Рассмотренный алгоритм можно улучшить, если избавиться от рекурсии и копирования значений.
Выполнение процедуры DFT можно представить следующим образом. Берутся пары элементов, вычисляется DFT каждой пары,
и пара заменяется своим DFT. В результате получается вектор, содержащий `n//2` 2-элементных DFT. Затем эти DFT
объединяются в пары, с помощью двух преобразований вычисляются DFT для каждых четырех элементов вектора, объединенных в четверки, после
чего два 2-элементных DFT заменяются одним 4-элементным DFT. Процесс продолжается до тех пор, пока
не получится два `n//2`-элементных DFT, которые с помощью `n//2` преобразований объединяются в конечное `n`-элементное DFT.
--
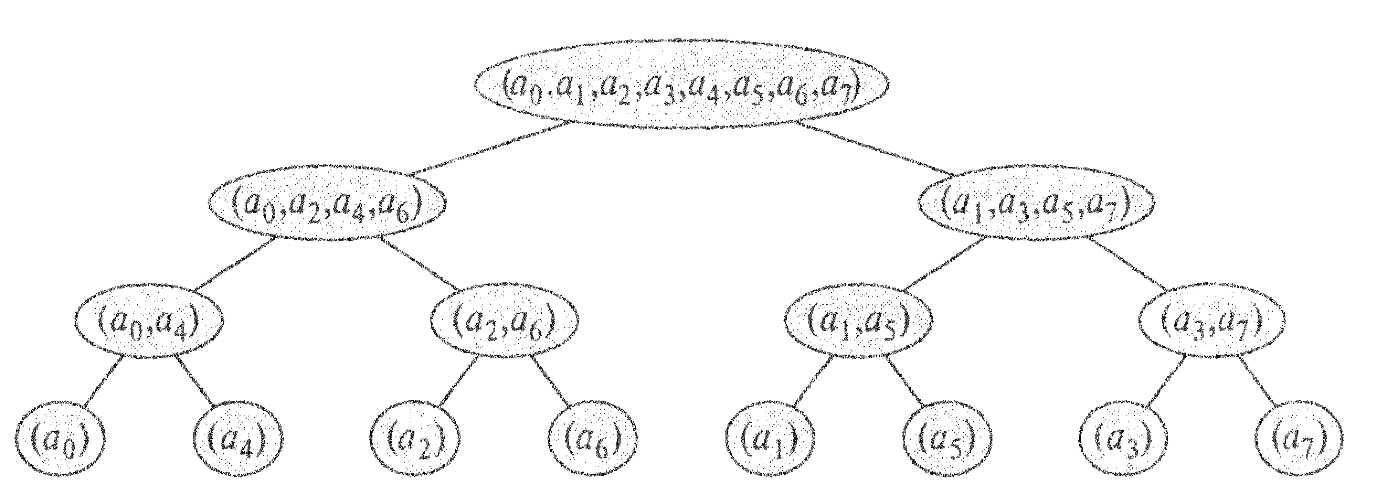
Для этого переставим элементы вектора `a` в том порядке, в котором они перечислены в листовых узлах дерева.
Это поразрядно обратная перестановка.
--
```c++
void fft (vector<complex<double>>& a, bool invert) {
int n = a.size();
for (int i=1, j=0; i<n; ++i) {
int bit = n >> 1;
for (; j>=bit; bit>>=1) j -= bit;
j += bit;
if (i < j) swap (a[i], a[j]);
}
for (int len=2; len<=n; len<<=1) {
double ang = 2*acos(-1.0)/len * (invert ? -1 : 1);
complex<double> wn(cos(ang), sin(ang));
for (int i=0; i<n; i+=len) {
complex<double> w(1);
for (int j=0; j<len/2; ++j) {
auto &a1=a[i+j];
auto &a2=a[i+j+len/2];
auto u = a1, v = a2*w;
a1 = u + v;
a2 = u - v;
w *= wn;
}
}
}
if (invert)
for (auto& ai:a) ai/= n;
}
```
--
```c++
void multiply (const vector<int>& a, const vector<int>& b, vector<int>& res) {
vector<complex<double>> fa(a.begin(), a.end()), fb(b.begin(), b.end());
int n = 1;
while (n < max(a.size(), b.size())) n <<= 1;
n <<= 1;
fa.resize(n); fb.resize(n);
fft(fa, false); fft(fb, false);
for (int i=0; i<n; ++i)
fa[i] *= fb[i];
fft(fa, true);
res.resize (n);
for (size_t i=0; i<n; ++i)
res[i] = round(fa[i].real());
}
```
--
Алгоритм легко распараллеливается:
--
Многоразрядные числа можно представить как полиномы `sum_{i=0}^n C_i*B^i`, где `B` -- основание системы счисления (10, 16 или 256), `C_i` `(0 <= C_i <B)` -- `i`-й разряд числа, и перемножить полиномы. После получения результата умножения полиномов нужно выполнить перенос старшей части коэффициентов в следующий коэффициент (разряд числа), так как коэффициент может достигать `n*B^2`. Таким образом умножение чисел можно выполнить за `O(n log n)`, что быстрее [алгоритма Карацубы](50959-4.html) за `O(n^{log_2 3})`, основанного на методе декомпозиции.
```c++
int p=0; // перенос
res.resize (n);
for (size_t i=0; i<n; ++i) {
p+= round(fa[i].real());
res[i]=p%B;
p/=B;
}
while(p>0) { // остались цифры
res.push_back(p%B);
p/=B;
}
```
При больших `n` возникает проблема неточности вычислений, но можно выполнять DFT в кольце по модулю `2^K+1` (алгоритм Фюрера, 2007 год), что усложняет алгоритм, и преимущество над алгоритмом Карацубы наблюдается только при `n>10000`.

 Начало
Начало Учебные материалы
Учебные материалы