Для полиномов можно определить множество разнообразных операций.
Суммой полиномов `A(x)` и `B(x)` степени `n` является полином `C(x)` степени `n`, такой что
`C(x) = A(x) + B(x)` для всех `x` из соответствующего поля.
Операция сложения выполняется за `O(n)` и для представления в виде вектора коэффициентов (`c_j=a_j+b_j`), и
для представления в виде значений в точках (`C.y_k=A.y_k+B.y_k`, при условии, что используется одинаковые наборы `x_k`)
--
Если `A(x)` и `B(x)` -- полиномы степени `n`, их *произведением* `C(x)` является полином
степени `2n`, такой что `C(x) = A(x)*B(x)` для всех `x` из соответствующего поля.
Например, умножение полиномов `A(x) = 6x^3 + 7x^2 -10x + 9` и `B(x) = -2x^3 + 4x -5` можно выполнить следующим
образом:
--
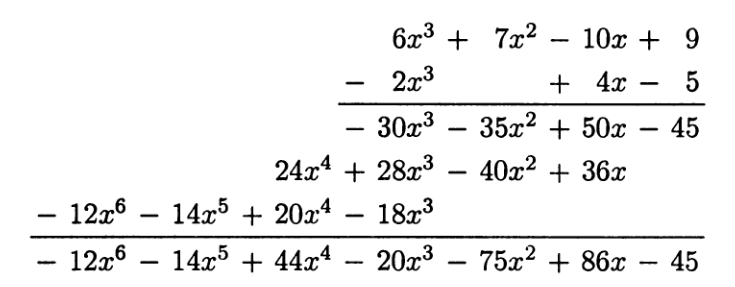
Операция умножения полиномов в коэффициентной форме оказывается гораздо более сложной, чем операции вычисления
полинома или сложения двух полиномов, поскольку каждый коэффициент из вектора `a` необходимо умножить на
каждый коэффициент из вектора `b`, что приводит к оценке `O(n^2)`.
Умножение для представлении в виде значений в точках выглядит проще -- достаточно перемножить значения в точках
`C.y_k=A.y_k*B.y_k`, но полином `C(x)` имеет степень `2n` и его представление должно содержать в 2 раза больше пар точка-значение.
Следовательно, необходимо использовать "расширенные" представления полиномов `A(x)` и `B(x)`, которые содержат по `2n+2` пар
точка-значение каждое.
--
Но как вычислить значение полинома, заданного в виде значений в точках, в некоторой новой точке?
По-видимому, для этой задачи не существует более простого подхода, чем преобразовать полином в коэффициентную
форму, а затем вычислить его значение в новой точке.
Полиномы
Начало
Учебные материалы