Подразделы

Другие разделы

Дата и время

09/04/2025 22:03:38

Авторизация

Численные алгоритмы

Вычислительная математика Классификация ошибок вычислений Алгоритмы численного интегрирования Алгоритмы для решения нелинейных уравнений Алгоритмы для поиска экстремума

Алгоритмы для решения нелинейных уравнений

Рассмотрим несколько алгоритмов для решения нелинейных уравнений с одним неизвестным $f(x) = 0$ .

Мы можем интерпретировать корень уравнения как точку, в которой график функции $f(x)$ пересекается с осью абсцисс $X$ .

График $f(x)$ может пересекать ось абсцисс в одной точке, многих или даже в бесконечном количестве точек (например, $sin x =0$ ) или не пересекать ее вообще ( $e^x =0$ ). Соответственно, уравнение будет иметь один корень, несколько корней или не иметь корней вовсе.

Перед тем как начинать поиск корней функции, нужно нарисовать её график. Это может помочь определить количество корней и их приближенное местоположение. В общем случае нужно определить интервалы, содержащие по одному корню рассматриваемого уравнения.

Метод деления пополам основан на наблюдении, что график непрерывной функции должен пересечь ось абсцисс между двумя точками $a$ и $b$ как минимум один раз, если значения функции имеют в этих точках разные знаки.

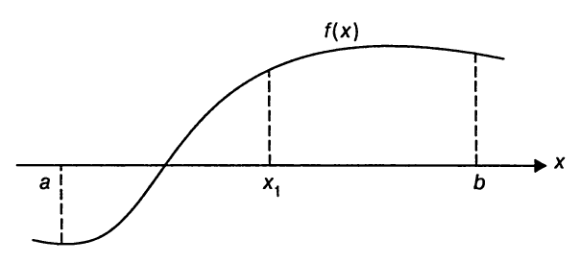
width:400px|Попалам

Начиная с отрезка $[a, b]$ , на концах которого $f(x)$ имеет разные знаки, алгоритм вычисляет среднюю точку $x_{m} = (a + b)//2$ . Если $f(x_{m}) = 0$ , корень найден, и алгоритм завершает работу. В противном случае он продолжает поиск корня либо на отрезке $[a,x_{m}]$ , либо на отрезке $[x_{m},b]$ — в зависимости от того, на какой из двух половин отрезка функция $f(x)$ имеет разные знаки на концах.

Поскольку мы не можем ожидать, что алгоритм "наткнется" на точное решение уравнения и завершит работу, нужен иной критерий для его завершения.

Можно остановиться, когда отрезок $[a_n,b_n]$ , содержащий некоторый корень $x^{**}$ , станет столь мал, что можно гарантировать, что абсолютная ошибка приближения $x^{**}$ величиной $x_n$ (средней точкой отрезка) меньше некоторого заранее выбранного значения $epsilon> 0$ . Поскольку $x_n$ — средняя точка отрезка $[a_n, b_n]$ и $x^{**}$ лежит внутри этого отрезка, мы имеем

$|x^{**}-x_n|<=(b_n-a_n)//2$

Следовательно, мы можем завершать работу алгоритма, как только $(b_n-a_n)//2<epsilon$ или $x_n-a_n<epsilon$ .

Нетрудно доказать, что

$|x^{**}-x_n|<=(b-a)/2^n$

То есть последовательность ${x_n}$ сходится к корню $x^{**}$ . На практике, если мы выберем значение $epsilon$ меньше ошибки округления, алгоритм может никогда не завершиться!

Поэтому вместо явного задания $epsilon$ часто ограничивают количество итераций, которое может выполнить алгоритм $n=|~ log_2 (b-a) - log_2 epsilon ~|$

Алгоритм Bisection( $f, a, b, n$ )
// Входные данные: непрерывная на $[a, b]$ функция $f(x)$ ,
// $f(а)*f(b) < 0$ , количество итераций $n$
// Выходные данные: Приближенное значение $x$
// корня уравнения $f(x)=0$ на отрезке $[a,b]$
while $n>0$ do
$quad x larr (a + b)//2$
$quad val larr f(x)$
$quad$ if $val = 0$
$quad quad$ return $x$
$quad$ if $val*f(a) <0$
$quad quad b larr x$
$quad$ else
$quad quad a larr x$
$quad n larr n-1$
return $a$

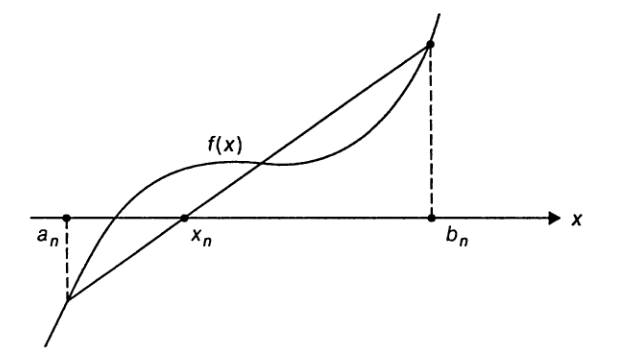
width:400px|Хорды

В отличие от метода деления пополам в методе хорд очередное приближение вычисляется как точка пересечения оси абсцисс с прямой линией, проведенной через точки $(a_n, f(a_n))$ и $(b_n, f(b_n))$ :

$x_n=(a_n*f(b_n)-b_n*f(a_n))/(f(b_n)-f(a_n))$

Задания для практики

Примените метод деления пополам для поиска корня уравнения $х^3+х-1 = 0$ с абсолютной ошибкой меньшей `10^{-2}.