Этапы решения алгоритмической задачи. Базовые структуры данных

Деревом называется связный ациклический граф. Для некоторых алгоритмов используется лес - граф, в котором каждая компонента связности является деревом.

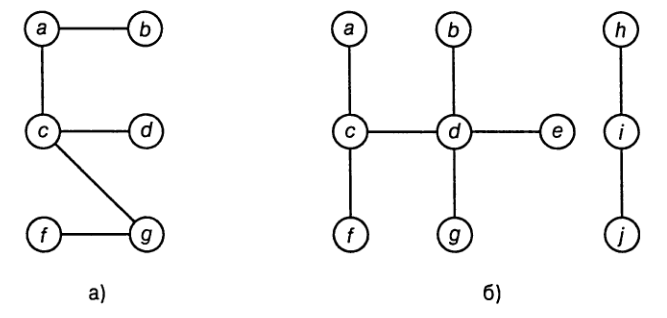
Число ребер в дереве всегда на единицу меньше, чем число его вершин.

Любую вершину в дереве можно назначить корнем и построить так называемое корневое дерево. Корень располагается вверху, на нулевом уровне дерева. Ниже корня располагаются смежные с ним вершины, составляющие первый уровень дерева. Вершины, соединенные с корнем через два ребра, составляют второй уровень дерева, и т.д.

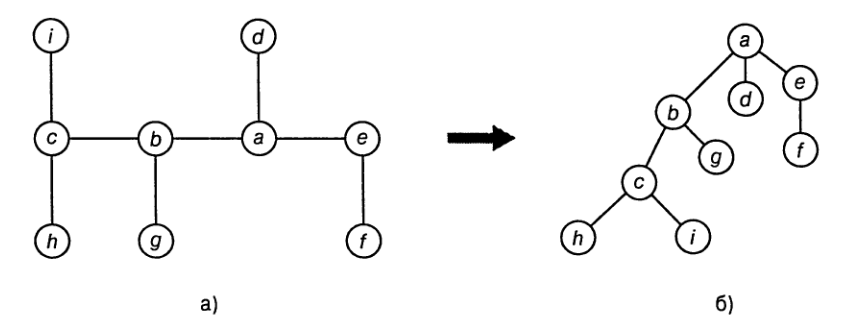
Корневые деревья используются в информатике для описания иерархических структур, таких как структура каталогов файловой системы, структура HTML-страницы (DOM).

Все вершины, принадлежащие маршруту от корня дерева до вершины `v`, называются предками вершины `v`. Совокупность всех вершин, для которых вершина `v` является предком, называют потомками `v`. Вершина, у которой нет потомков, называется листом.

Глубина вершины `v` вычисляется как длина пути от корня до этой вершины. Высота дерева вычисляется максимальная глубина для листьев дерева.

Упорядоченным называется такое корневое дерево, в котором важен порядок потомков каждой вершины. Двоичное (бинарное) дерево можно определить как упорядоченное дерево, каждая вершина которого имеет не более двух потомков, причем каждый из потомков считается либо левым, либо правым потомком своего родителя.

Двоичным деревом поиска называют двоичное дерево, каждой вершине которой назначено число, которое больше, чем число, назначенное ее левому потомку, и меньше, чем число, назначенное ее правому потомку.

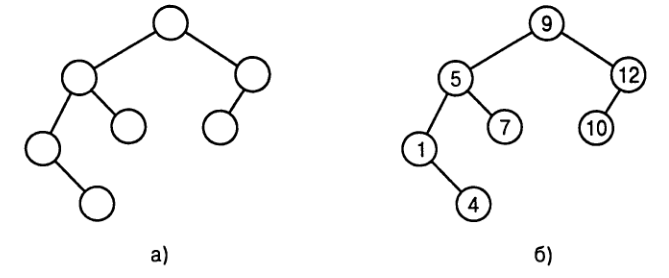
В программах бинарные деревья реализуют в виде структуры данных, узлы которой соответствуют вершинам дерева и содержат связянную с ней информацию, а также два указателя на его левого и правого потомка.

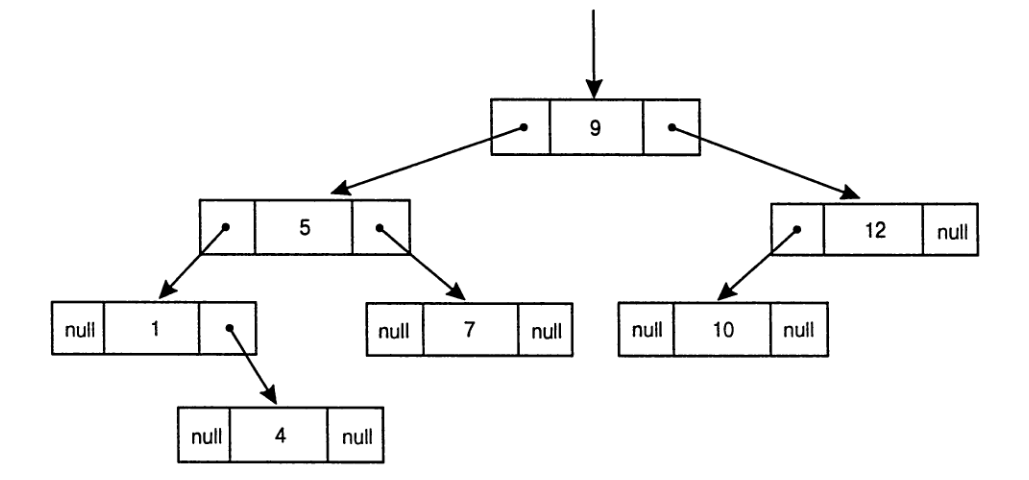
Для упрощения операций можно сделать дополнительные указатели на родительские узлы.

Произвольное упорядоченное дерево можно представить как двоичное, левый указатель будет содержать ссылку на первого потомка текущей вершины, а правый — на следующую родственную ей вершину.

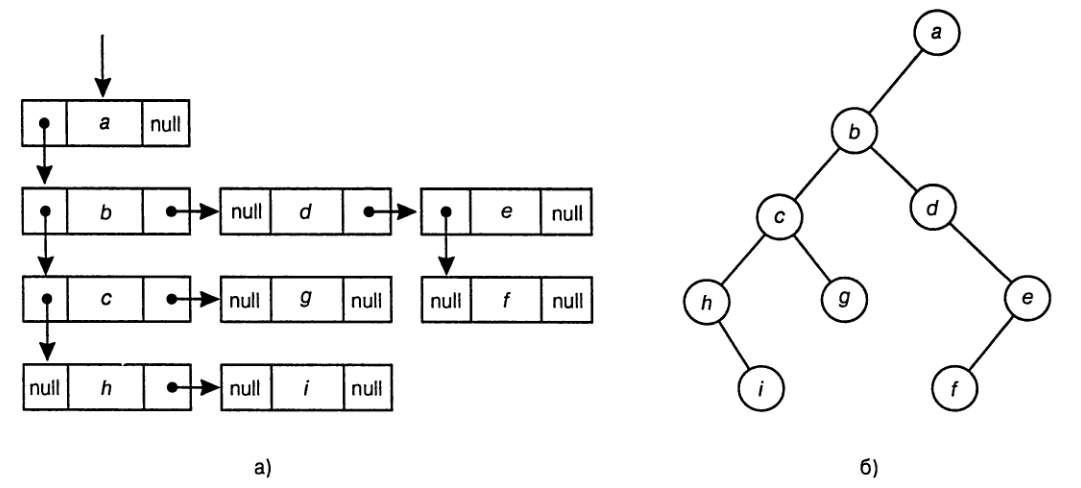
Также можно добавить два указателя на родительский узел и предыдущую родственную вершину (DOM).