Этапы решения алгоритмической задачи. Базовые структуры данных

Алгоритм является процедурным решением задачи.

Такое решение является не ответом, а инструкциями для получения ответа. Именно этот акцент отличает информатику от других дисциплин, в частности от математики, в которой обычно ограничиваются доказательством существования решения и (иногда) исследованиями характеристик решения.

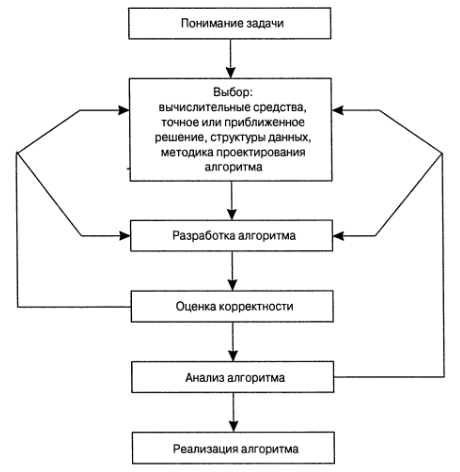
Сравнение процессов решения алгоритмических и математических задач

Понимание задачи

С практической точки зрения, прежде чем заняться проектированием алгоритма, необходимо полностью понять поставленную перед вами задачу. Прочтите внимательно условие задачи и задайте вопросы, если вы чего-то не поняли. Просчитайте вручную несколько небольших примеров, продумайте частные случаи и при необходимости снова задайте вопросы.

Если перед вами поставлена одна из типовых задач, для ее решения можно воспользоваться известным алгоритмом.

Области определения для входных данных должны учитываться в алгоритме. Если этого не сделать, то алгоритм может работать для большинства значений входных параметров, однако при подстановке отдельных "граничных" значений вы получите некорректные результаты.

Определение возможностей вычислительного устройства

Полностью уяснив суть поставленной задачи, необходимо оценить возможности вычислительного устройства, для которого создается алгоритм.

Большинство современных алгоритмов предназначено для работы на компьютерах с архитектурой фон Неймана, на которых в каждый момент времени может выполняться только одна команда. Такие алгоритмы являются последовательными. Для компьютеров, которые могут одновременно выполнять несколько команд, разрабатываются параллельные алгоритмы.

Необходимо учитывать быстродействие компьютера и доступный объем оперативной памяти.

Выбор между точным или приближенным методом решения задачи

Почему для решения задачи иногда выбираются приближенные алгоритмы? Во-первых, существуют задачи, которые нельзя решить точно Например, извлечение квадратного корня, решение нелинейных уравнений. Во-вторых, существующие алгоритмы для точного решения задачи могут быть недопустимо медленными. Классической из таких задач является задача коммивояжера, которая заключается в поиске кратчайшего маршрута между `n` городами.

Выбор подходящих структур данных

В некоторых алгоритмах не требуется, чтобы входные данные были представлены в каком-то специфическом формате. Однако для работы многих алгоритмов требуются совершенно определенные структуры данных. Cтруктуры данных непосредственно влияют на процесс программирования. ООП предполагает определение структур до написания алгоритмов.

Методы проектирования алгоритмов

Изучение этих методов в высшей степени важно по следующим причинам.

Во-первых, они обеспечивают набор универсальных принципов, руководствуясь которыми можно разработать алгоритмы решения новых задач, т.е. таких задач, для решения которых еще не существует достаточно хороших алгоритмов. Эти методов сродни подаренной удочке, а не рыбе.

Во-вторых, алгоритмы являются краеугольным камнем информатики. Классификация основополагающих понятий важна для любой науки, и информатика не является исключением.

Методы представления алгоритмов

После того как алгоритм спроектирован, нужно представить его в каком-либо виде: на естественном языке, в виде псевдокода или схемы.

Присущая любому естественному языку неопределенность иногда затрудняет лаконичное и понятное описание алгоритмов.

Схемы алгоритмов (flowchart) в современной литературе не используются, так как они становятся слишком громоздкими в случае больших и сложных алгоритмов (хотя и наглядны см. рисунок выше)

Описание алгоритма на псевдокоде обычно является более точным по сравнению с естественным языком. Странно, что специалисты до сих пор так и не приняли какую-либо форму псевдокода в качестве стандарта и в книгах можно встретить различные "диалекты" этого языка.

Алгоритм НОД(`m, n`)
while `n!=0` do
`quad r larr m mod n`
`quad m larr n`
`quad n larr r`
return `m`

Для создания программы необходимо вручную переписать алгоритм на какой-то из языков программирования, так как ни одно из описаний не может быть понято компьютером.

Оценка корректности алгоритма

После представления алгоритма в какой-либо форме, необходимо оценить его корректность. Это означает, что вы должны доказать, что выбранный алгоритм за ограниченный промежуток времени выдает требуемый результат для любых корректных значений входных данных.

Например, корректность алгоритма Евклида для вычисления НОД двух чисел следует из правильности равенства `gcd (m, n) = gcd (n, m mod n)`, а также из простого наблюдения, что второе число на каждой итерации будет все время уменьшаться, и по достижении им нуля, выполнение алгоритма прекращается.

Доказать корректность одних алгоритмов очень легко, других — невероятно сложно. Универсальным методом доказательства корректности алгоритма считается метод математической индукции, так как алгоритмы обычно являются итеративными.

Хотя доказательством некорректной работы алгоритма может служить лишь один набор входных данных, при обработке которых получается неправильный результат, доказать с помощью набора входных данных корректность алгоритма нельзя. Но правильно подобранный набор входных данных может дать оценку быстродействия алгоритма.

Оценка корректности приближенных алгоритмов сложнее, чем точных, так как при этом нужно показать, что погрешность получаемых в результате работы алгоритма выходных данных не превышает заранее установленных пределов.

Анализ алгоритма

Обычно создатели алгоритмов стараются, чтобы они удовлетворяли нескольким требованиям. После проверки корректности алгоритма одной из самых важных характеристик является оценка его эффективности. На практике существует два вида оценки эффективности алгоритма: временная и пространственная.

Еще одной важной характеристикой алгоритма является его простота. Её нельзя оценить с помощью строгих математических выражений, и такая оценка будет всегда субъективна. Например, поиск НОД двух чисел с помощью разложения на простые множители для 6-классника понятнее и проще, но даже начинающий программист предпочтет алгоритм Евклида.

Тем не менее к простоте нужно стремиться, потому что простые алгоритмы

• легче понять и запрограммировать;
• содержат меньше строк и, следовательно, ошибок;
• более эффективны, чем их сложные аналоги;
• имеют эстетическая привлекательность.

Следующей важной характеристикой алгоритма является его универсальность, на которую влияют два момента:

• общность задачи, для решения которой разработан алгоритм;
• диапазон допустимых значений его входных данных.

Иногда легче разработать алгоритм для решения общей задачи, чем заниматься поиском решения ее частного случая. Например, для проверки взаимной простоты двух целых чисел лучше написать алгоритм вычисления НОД и проверить, равен ли результат 1. С другой стороны, алгоритм для поиска корней квадратного уравнения нельзя обобщить для поиска корней полиномов более высоких степеней.

Диапазон изменения значений входных данных может колебаться в очень широких пределах и должен естественным образом соответствовать решаемой задаче. Например, алгоритм для поиска корней квадратного уравнения можно использовать и в случае отрицательного дискриминанта, но обычно этот случай исключают из рассмотрения, поскольку он должен оговариваться отдельно.

Если вас не устраивает эффективность, простота или универсальность алгоритма, то придется перепроектировать алгоритм.

Конструктор достигает совершенства не тогда, когда ему больше нечего добавить к своему детищу, а тогда, когда больше ничего удалить

Антуан де Сент-Экзюпери

Кодирование алгоритма

В конечном итоге алгоритм должен быть превращен в компьютерную программу. В процессе написания программы могут быть внесены ошибки, либо отдельные шаги алгоритма реализованы неэффективно.

Корректность программы может быть проверена с помощью тестирования.

Неэффективность реализации частично может решена с помощью современных компиляторов, которые могут оптимизировать код, вынося вычисления инвариантного выражения за пределы цикла, но производительность при этом может увеличиться только на 10-50%, тогда как использование более эффективного алгоритма иногда ускоряет выполнение программы на несколько порядков.

Достижение идеала — это сложная задача, и часто приходится использовать компромиссное решение, так как время разработки также является одним из ресурсов.

Для конкретного алгоритма легко вычислить его эффективность, сложнее ответить на вопрос, какова оптимальность алгоритма для этой задачи, существует ли алгоритм с лучшей эффективностью?

Для некоторых задач ответ на этот вопрос найден. Например, определено, что сортировка `n` произвольных элементов требует `n * log_2 n` операций. Для задачи перемножения матриц вопрос остается открытым. Простейший алгоритм требует `n^3` операций, но были придуманы алгоритмы с лучшей эффективностью (`n^{2.372}` в 2020 году), но все они из-за сложности эффективны только для матриц размерности более 100.