Начало
Учебные материалы
Этапы решения алгоритмической задачи. Базовые структуры данных
Этапы решения алгоритмической задачи Важные типы задач Линейные структуры данных Графы Деревья Множества и словари
Графы
соединена линиями или стрелками.
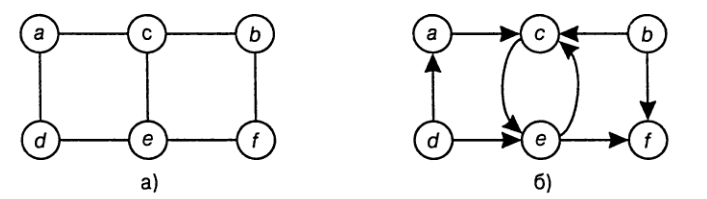
Математически граф `G(V, E)` есть совокупность двух множеств:
* конечное непустое множество элементов V, называемых *вершинами*;
* множества Е, содержащего пары `(u,v)`, где `u,v in V`, называемые *ребрами*.
Если вершины в паре неупорядочены, т.е. пара `(u, v)` означает то же самое,
что и пара `(v, u)`, то граф `G` называют неориентированным.
Если порядок в паре важен, то граф `G` называют ориентированным (орграфом). Ребра в орграфе называют *дугами*.
--
Ребра, начинающиеся и заканчивающиеся в одной вершине называются *петлями*.
Граф, в котором каждая пара вершин соединяется ребром, называется
*полным*. В полном графе количество ребер равно `k=(n*(n-1))/2`, где `n` - количество вершин в графе.
Граф, в котором количество ребер близко к `k`, называется *плотным*.
Граф, в котором количество ребер близко к `n`, называется *разреженным*.
От того, является граф плотным или разреженным, зависит
способ его представления и выбор используемого для решения задачи алгоритма.
--
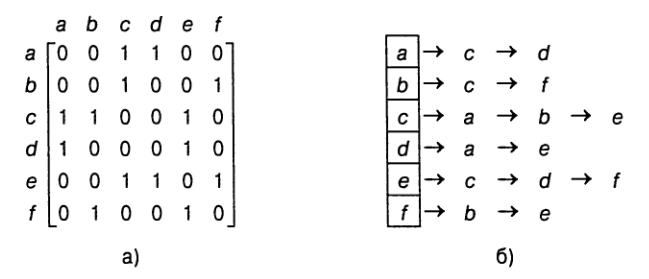
*Матрица смежности* используется для представления плотных графов и представляет
собой булеву матрицу размером `n xx n`, в которой каждая строка и каждый столбец соответствуют одной из вершин
графа. Элемент этой матрицы, находящийся на пересечении `i`-ой строки и `j`-ro
столбца, равен 1 в случае, если `i`-я и `j`-я вершины графа соединяются ребром,
и 0 в противном случае.
*Cписки смежных вершин* предпочтительно использовать для разреженных графов.
Это одномерный массив, каждый элемент которого соответствует одной из вершин графа и
содержит список всех смежных вершинах текущей вершины. В списках присутствуют вершины
графа, которым в матрице смежности соответствуют единичные элементы.
--
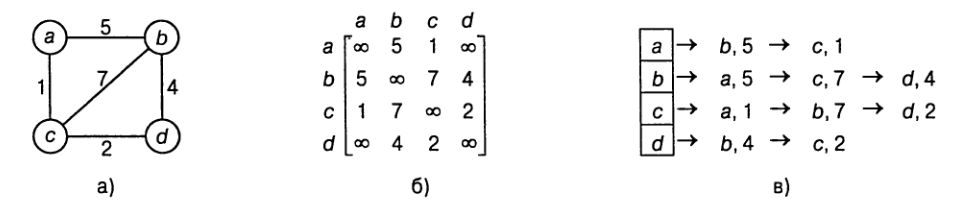
Под *взвешенным графом* подразумевается граф, ребрам которого поставлены в соответствие числа, которые могут означать
*вес* или *стоимость* или *пропускную способность* ребра. Оба способа представления легко приспособить для случая взвешенных графов.
Элемент *матрицы весов* `A_{ij}` должен равняться весу ребра, соединяющего `i`-ю и `j`-ю вершины. Если вершины не соединены ребром, то
элемент `А_{ij}` должен содержать какое-нибудь специальное значение `+oo` или 0. Для списков смежных вершин в каждый узел списка
нужно включить не только номер смежной вершины, но и вес соответствующего ребра.
--
Граф называется *связным*, если для любой пары его вершин `u` и `v` существует путь от `u` к `v`. Граф,
не содержащий циклов, называют *ациклическим*.
