 Разбор задач
Разбор задач
 1. Черно-белая графика
1. Черно-белая графика
Простая задача на технику программирования.
Так как во входных данных значения для пикселов изображений не разделены пробелами, то проще использовать тип string для хранения строк изображений. Аналогично можно поступить с информацией о логической операции. Описание переменных и ввод выглядит так:
var
p1,p2:array[1..100]of string; { Изображения }
op:string; { Логическая операция }
w,h,i,j:integer; { Размеры и переменные цикла }
...
{Ввод}
for i:=1 to h do
readln(p1[i]);
for i:=1 to h do
readln(p2[i]);
readln(op);
Вычисление результата можно совместить с выводом. Для перевода символа c в число используется выражение ord(c)-ord('0').
for i:=1 to h do
begin
for j:=1 to w do
write(op[(ord(p1[i][j])-ord('0'))*2+(ord(p2[i][j])-ord('0'))+1]);
writeln;
end;
 2. Газон
2. Газон
Задача средней сложности, на эффективный алгоритм.
Простая проверка всех точек прямоугольника по отдельности на попадание в круг не эффективна, необходимо добавлять точки отрезками. Для этого рассматриваем все `x`, которые попадают в область пересечения, и находим минимальную и максимальную ординаты точек с выбранным `x`. К результату добавляем `y_max-y_min+1`.
var res:int64; { ответ может быть больше, чем 2*10^9 }
...
res:=0;
for x:=max(x1,x3-r) to min(x2,x3+r) do
begin
d:=trunc(sqrt(sqr(extended(r))-sqr(extended(x3-x))));
ymin:=max(y1,y3-d);
ymax:=min(y2,y3+d);
if ymin<=ymax then
res:=res+ymax-ymin+1;
end;
Перед возведением в квадрат число преобразуется в вещественное, чтобы избежать переполнения. Функции max и min вычисляют максимум и минимум из двух чисел.
 3. Трамвай
3. Трамвай
Сложная задача, необходимо использовать специальные структуры данных.
Фактически нужно промоделировать поездку трамвая. Когда пассажир входит в трамвай, если есть свободное место, и его `a_i-b_i\ >\ 0`, то он садится, иначе ищем среди сидящих пассажиров пассажира с минимальной разностью `a_i-b_i`. Если эта разность окажется меньше, чем у вошедшего, то этот пассажир должен уступить место вошедшему. Когда сидящий пассажир выходит из трамвая, то его место занимает пассажир с наибольшей положительной разностью `a_i-b_i` среди стоящих.
Для быстрого нахождения пассажира с минимальной разностью среди сидящих и максимальной разностью среди стоящих в C++ можно использовать класс STL set, который реализован на красно-черных деревьях. Реализовать эту структуру на Паскале очень сложно, но для данной задачи можно использовать гораздо более простое дерево сумм, которое позволяет находить `m`-ое по величине значение в наборе за логарифмическое время. Выглядит это дерево так:
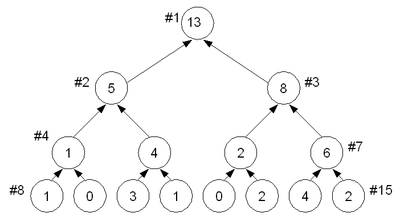
В вершине с номером `k` хранится сумма значений в вершинах с номерами `2*k` и `2*k+1`. При изменении значений в листьях дерева в нижней строке, корректное состояние дерева восстанавливается за логарифмическое время.
Разность `a_i-b_i` не превышает `2\ 000\ 000` (отрицательные разности обрабатываются отдельно), поэтому храним дерево в массиве размером `4\ 194\ 303`, элементы с 1 по `2\ 097\ 151` хранят узлы дерева, а элементы с `2\ 097\ 152` по `4\ 194\ 303` – листья. Для обращения к нужному листу, хранящему количество пассажиров с некоторой разностью, нужно добавить к разности `2\ 097\ 152`
var sumtree:array[1..4194303] of longint;
...
k:=pass[j].a-pass[j].b+2097152;
if pass[j].c=i then
inc(sumtree[k]) { пассажир вошел }
else
dec(sumtree[k]); { пассажир вышел }
{ восстанавливаем корректность дерева }
while k>1 do
begin
k:=k div 2;
sumtree[k]:=sumtree[2*k]+sumtree[2*k+1];
end;
Для нахождения разности у `m`-го пассажира в отсортированном по разности наборе используем следующий код:
if sumtree[1] < m then
difm:=0 { пассажиров с положительной разностью меньше m }
else
begin
k:=1;
mm:=m;
while k<2097152 do
begin
k:=2*k+1; { переходим к правому потомку узла }
if sumtree[k]<mm then
begin { в правом потомке менее mm пассажиров }
mm:=mm-sumtree[k];
dec(k); { выбираем левого потомка }
end;
end;
difm:=k-2097152;
end;
После добавления или удаления пассажира проверяем как изменилась разность у `m`-го пассажира и изменяем сумму разностей сидящих пассажиров.
if pass[j].c=i then
begin { пассажир вошел }
if oldifm<pass[j].a-pass[j].b then { занял чье-то место }
sumd:=sumd+pass[j].a-pass[j].b-oldifm
end
else
begin { пассажир вышел }
if difm<pass[j].a-pass[j].b then { на его место кто-то сел }
sumd:=sumd-(pass[j].a-pass[j].b)+difm;
end;
oldifm:=difm;
Вместо написания быстрой сортировки пассажиров по номерам остановок, на которых они входят и выходят, можно сделать разделение пассажиров по спискам, соответствующим остановкам.
var
sl:array [1..100001] of integer; { номера первых пассажиров в спиcках }
pass:array [1..100000] of record
a,b,c,d:longint;
nextin,nextout:longint; { номер следующего в списке }
end;
...
{ Ввод и распределение по спискам }
readln(N,M,S);
for i:=1 to N do
begin
readln(pass[i].a,pass[i].b,pass[i].c,pass[i].d);
pass[i].nextin:=sl[pass[i].c];
sl[pass[i].c]:=i;
pass[i].nextout:=sl[pass[i].d];
sl[pass[i].d]:=i;
end;
Обработка списка для каждой остановки и вычисление результата выглядит так:
res:=0;
sumd:=0; { сумма разностей у сидящих }
sumb:=0; { сумма b[i] у всех пассажиров трамвая }
oldifm:=0;
for i:=1 to S do
begin
j:=sl[i]; { индекс первого пассажира,
вошедшего или вышедшего на i-ой остановке }
while j<>0 do { список не закончился }
begin
if pass[j].a>pass[j].b then
begin
{ модифицируем дерево сумм }
...
{ пересчитываем сумму разностей сидящих пассажиров }
...
end;
if pass[j].c=i then
begin { пассажир вошел }
sumb:=sumb+pass[j].b
j:=pass[j].nextin; { к следующему в списке }
end
else
begin { пассажир вышел }
sumb:=sumb-pass[j].b;
j:=pass[j].nextout; { к следующему в списке }
end;
end;
res:=res+sumd+sumb;
end;
writeln(res);
В операторе res:=res+(sumd+sumb); при сложении суммы разностей `a_i-b_i` для сидящих (sumd) и суммы `b_i` для всех пассажиров (sumb) получается сложение сумма `a_i` для сидящих и сумма `b_i` для стоящих.
 4. Треугольники
4. Треугольники
Сложная задача, необходимо знание алгоритма быстрой сортировки.
Сначала докажем, что треугольник с целочисленными координатами вершин равносторонним быть не может. Площадь равностороннего треугольника равна `{a^2\ sqrt(3)}/4`, где `a` – длина стороны. Для вершин с целыми координатами `a^2` будет целым, следовательно площадь равностороннего будет выражаться иррациональным числом. Площадь многоугольника с целочисленными координатами вершин может быть вычислена по формуле Пика как `p\ +\ q/2\ -\ 1`, где `p` – количество точек с целочисленными координатами внутри многоугольника, а `q` – на границе многоугольника, включая вершины. Площадь треугольника с целочисленными координатами вершин будет рациональным числом. Получили противоречие, следовательно, можно при решении задачи не рассматривать равносторонние треугольники.
Возьмем какую-нибудь точку из заданного множества и отсортируем остальные вершины по квадрату расстояния до нее. Для сортировки необходимо использовать быструю сортировку со временем работы `O(N\ log\ N)`. Если существует `k` точек, лежащих на одинаковом расстоянии от выбранной точки, то из них можно составить `{k*(k-1)}/2` равнобедренных треугольников. Из этого количества нужно вычесть вырожденные треугольники, образованные центрально-симметричными точками относительно выбранной. Для этого либо сравниваем попарно положения точек, лежащих на одинаковом расстоянии от выбранной (сложность такого сравнения `O(N^2)`, но из-за геометрической основы задачи общее количество таких сравнений будет небольшим и общее время работы алгоритма не ухудшится), либо отсортировать после ввода все точки по `x`, затем по `y` и выполнять поиск центрально-симметричной точки относительно выбранной точки для всех остальных точек за время `O(log\ N)`.
Такие действия необходимо выполнить для всех точек, время работы алгоритма с использованием двух сортировок равно `O(N^2\ log\ N)`. Основная часть решения выглядит так:
var N,i,j,k,m,jj:longint;
x,y:array[1..1500] of longint;
d:array[1..1500] of record d:int64;x,y:longint; end;;
res:int64;
...
{ ввод данных }
readln(N);
for i:=1 to N do
readln(x[i],y[i]);
res:=0;
for i:=1 to N do
begin
{ заполняем массив с расстояниями и относительными координатами }
k:=0;
for j:=1 to N do
if i<>j then
begin
inc(k);
d[k].d:=sqr(int64(x[i]-x[j]))+sqr(int64(y[i]-y[j]));
d[k].x:=x[j]-x[i];
d[k].y:=y[j]-y[i];
end;
{ сортировка }
qsort(1,k);
j:=1;
while j<=k do
begin
{ считаем количество точек на одинаковом расстоянии }
m:=1;
while (j+m<=k) and (d[j].d=d[j+m].d) do
begin
{ вычитаем вырожденные треугольники }
for jj:=j to j+m-1 do
if (d[j+m].x=-d[jj].x) and (d[j+m].y=-d[jj].y) then
dec(res);
inc(m);
end;
res:=res+m*(m-1) div 2;
j:=j+m;
end;
end;
writeln(res);
 5. Клавиатура
5. Клавиатура
Очень простая задача.
Считываем ограничения на число нажатий каждой клавиши в массив `c`, затем считываем номера нажатых клавиш и уменьшаем на 1 значения соответствующих элементов в массиве `c`. По окончании просматриваем массив `c` и для отрицательных элементов выводим "no", для неотрицательных – "yes".
Основные ошибки были связаны с неправильным размером массива для последовательности нажатых клавиш и неправильным типом для переменной цикла (byte вместо longint).
 6. Неправильное сложение
6. Неправильное сложение
Задача средней сложности на перебор, технику программирования.
Для описанного в задаче способа сложения выполняется свойство коммутативности, поэтому достаточно рассмотреть три варианта сложения трех чисел: `(a+b)+c`, `(a+c)+b` и `(b+c)+a`. Полученные три результата сортируем по возрастанию (для сравнения чисел, хранящихся в string, можно использовать выражение (length(s1)>length(s2)) or (length(s1)=length(s2)) and (s1>s2)), выбрасываем одинаковые результаты. Если остался один результат, выводим "NO", иначе "YES". Функцию для сложения двух чисел можно определить так:
function sum(s1,s2:string):string;
var r:string;
i,p:integer;
begin
{выравниваем числа по длине }
while length(s1)<length(s2) do s1:='0'+s1;
while length(s1)>length(s2) do s2:='0'+s2;
{ складываем }
r:='';
for i:=length(s1) downto 1 do
begin
p:=ord(s1[i])+ord(s2[i])-2*ord('0');
r:=chr(p mod 10+ord('0'))+r;
if p>=10 then
r:='1'+r;
end;
sum:=r;
end;
 7. Числа
7. Числа
Задача средней сложности на динамическое программирование.
Если существует `k` способов получить последовательность из `(i-1)` символа и число с позиции `i` до позиции `j` не превышает `C`, то `k` способов должно быть добавлено к числу способов получения последовательности из `j` символов. Суммирование нужно выполнять по модулю `10^k`. Рассматриваем все возможные `i` и `j` `(0\ ≤\ i\ ≤\ j\ ≤\ n)` и заполняем таблицу `t` с результатами. По окончании выводим значение `t_n`.
var
c,n,k,v,i,j:longint;
s:string;
t:array[0..50000] of int64;
p:int64;
...
readln(n,c,k);
readln(s);
{ вычисляем 10^k }
p:=1;
for i:=1 to k do
p:=p*10;
{ основной цикл: заполнение таблицы }
t[0]:=1;
for i:=1 to n do
begin
v:=0;
for j:=i to n do
begin
{ увеличиваем значения всех ячеек, достижимых с позиции i }
v:=v*10+ord(s[j])-ord('0');
if v>c then break;
t[j]:=(t[j]+t[i-1]) mod p;
if s[i]='0' then break; { c 0 достижима только следующая ячейка }
end;
end;
writeln(t[n]);
 8. Перестановки
8. Перестановки
Сложная задача на динамическое программирование, представление множеств в виде двоичных чисел.
Для нахождения НОД двух чисел используем следующую функцию.
function gcd(a,b:longint):longint; begin if b=0 then gcd:=a else gcd:=gcd(b, a mod b); end;
Чтобы ускорить вычисления, можно заполнить результаты вычисления НОД для элементов множества в таблице.
var
_gcd:array[1..16,1..16]of longint;
...
for i:=1 to n do
for j:=1 to n do
_gcd[i,j]:=gcd(p[i],p[j]);
Использование при реализации алгоритма динамического программирования запоминающей ранее вычисленные результаты функции позволяет не заботиться о правильном порядке заполнения таблицы с результатами для отдельных подзадач.
Функция count вычисляет количество `k`-перестановок подмножества из элементов, заданных параметром mask (в `j`-м бите числа стоит 1, если в подмножесто входит `(j+1)`-й элемент исходного множества), в которых на первом месте стоит `i`-й элемент исходного множества.
var
c:array[1..16,1..65535]of int64; { таблица с результатами подзадач }
...
function count(i,mask:longint):int64;
var j:longint;
begin
if c[i,mask]<0 then { значение еще не вычислялось }
begin
c[i,mask]:=0;
for j:=1 to n do
if (i<>j) and
((mask and (1 shl (j-1)))<>0) and { есть в подмножестве }
(_gcd[i,j]>=k) { НОД > k }
then
{ j-й элемент можно поставить следующим после i-го }
c[i,mask]:=c[i,mask]+count(j,mask and not(1 shl (i-1)));
end;
count:=c[i,mask];
end;
...
{ начальная заполнение таблицы }
mask:=(1 shl n)-1;
for i:=1 to n do
for j:=1 to mask do
c[i,j]:=-1; { вычисления не выполнены }
for i:=1 to n do
c[i,1 shl (i-1)]:=1; { существует только одна перестановка из одного элемента }
После ввода необходимо отсортировать элементы множества, чтобы рассматривать перестановки в лексикографическом порядке.
var
p:array[1..16]of longint;
n,m,k,t,i,j,mask:longint;
...
read(n,m,k);
for i:=1 to n do
read(p[i]);
for i:=1 to n do
for j:=i+1 to n do
if p[i]>p[j] then
begin
t:=p[i];
p[i]:=p[j];
p[j]:=t;
end;
После подготовительных операций выбираем, с какого элемента должна начинаться перестановка. Если количество перестановок, начинающихся с `j`-го элемента меньше `m`, рассматриваем в качестве кандидата `(j+1)`-й элемент, при этом из `m` вычитаем количество `k`-перестановок, начинающизся с `j`-го элемента. Если количество перестановок, начинающихся с `j`-го элемента больше или равно `m`, печатаем `j`-й элемент и убираем его из множества. Алгоритм выполняется, пока множество не опустеет, либо не будет найден ни один кандидат на первое место в перестановке.
var fl:boolean;
...
i:=0; { предыдущий элемент перестановки }
while mask<>0 do { пока не выведем все элементы из множества }
begin
fl:=false;
for j:=1 to n do
begin
if (i<>j) and
((mask and (1 shl (j-1)))<>0) and { есть в подмножестве }
((i=0) or (_gcd[i][j]>=k)) { НОД > k или 1 элемент перестановки }
then
begin
if m<=count(j,mask) then
begin { попали на нужный элемент }
write(p[j],' ');
i:=j;
mask:=mask and not(1 shl (j-1));
fl:=true;
break;
end
else
m:=m-count(j,mask);
end;
end;
if not fl then { нет подходящего элемента }
begin
writeln(-1);
halt(0);
end;
end;
writeln;

 Начало
Начало Соревнования
Соревнования