Подразделы

Другие разделы

Дата и время

05/04/2025 23:48:20

Авторизация

Зарегистрироваться
Восстановить пароль

Приближенные, рандомизированные и вероятностные алгоритмы

Приближенные алгоритмы для трудных задач Рандомизированные и вероятностные алгоритмы

Рандомизированные и вероятностные алгоритмы

Алгоритм будем называть рандомизированным, если его поведение определяется не только набором входных величин, но и значениями, которые выдает генератор случайных чисел. Будем использовать этот термин только для алгоритмов, которые дают точный результат, независящий от качества генератора случайных чисел.

Перемешивание входных данных

Ранее мы обсуждали, что для случайных массивов алгоритм быстрой сортировки работает быстрее, для отсортированных или почти отсортированных.

Поэтому повышения эффективности нужно либо добавить обмен $A[l]$ с $A["random"(l,r)]$ перед вызовом Partition, либо выполнить перемешивание перед вызовом QuickSort. Перемешивание работает за $Theta(n)$ и не ухудшит эффективность алгоритма сортировки.

Алгоритм Shuffle( $A$ )
// Входные данные: Массив $A[0...n-1]$
// Выходные данные: Массив $A[0...n-1]$ , в случайном порядке
for $i in [n-1...1]$ do
$quad "Обмен " A[i] " и " A["random"(0,i)]$

В данном случае мы получаем точное решение задачи. Рандомизация служит только для предотвращения худшего случая – его вероятность снижается до $1//n!$ .

Такое перемешивание можно применить перед построением двоичного дерева поиска, чтобы уменьшить его высоту, так как в худшем случае его высота может стать равной $n$ и поиск в дереве превратится в последовательный поиск. На практике вместо этого используют декартово дерево, в котором к узлам добавляется специальный случайный ключ, используемый для формирования дерева как в пирамиде.

В алгоритме максимального паросочетания рекомендуется сначала сделать случайное паросочетание, а затем улучшать его до максимального.

Вероятностный алгоритм – алгоритм, предусматривающий обращение на определённых этапах своей работы к генератору случайных чисел с целью получения экономии во времени работы за счёт замены абсолютной достоверности результата достоверностью с некоторой вероятностью или за счёт шанса получения результата за заданное время. Качество генератора случайных чисел влияет на качество работы вероятностного алгоритма.

Часто вероятностные алгоритмы используют для получения приближенного решения. Например, если мы не можем придумать хорошую жадную эвристику, можно получить несколько случайных решений и выбрать из них лучшее. Чем больше попыток мы делаем, тем точнее результат. В этом заключается метод Монте-Карло. Примеры: генетические алгоритмы, моделирование молекул.

Алгоритм Лас-Вегаса получает точный результат, но за счет случайного времени на решение. Можно указать только вероятность получения результата за заданное время. Примеры: недетерминистический алгоритм для $NP$ -задач, случайный поиск в задачах многомерной оптимизации, получение беспристрастных случайных бит от нестандартной монеты.

Тест простоты Миллера-Рабина

Малая теорема Ферма утверждает, что если число $n$ – простое, a $a$ – число, не делящееся на $n$ , то $a^{n-1)=1 (mod n)$ . Если $n$ не удовлетворяет этому уравнению для $a in [1...n-1]$ , то можно сказать наверняка, что это число составное. Однако существуют так называемые числа Кармайкла (первое из таких чисел $561=3*11*17$ ), для которых эта формула выполняется, но число является составным. Проблема решается небольшим изменением процедуры проверки. Мы должны проверить на нескольких числах выполнение малой теоремы Ферма, и чем больше таких проверок мы сделаем, тем больше уверенность, что число $n$ – простое.

Алгоритм PrimeTestMillerRabin( $n, s$ )
// Входные данные: $n>2$ – нечетное число, s – количество проверок
for $j in [1...s]$ do
$quad a larr "random"(2, n-1)$
$quad$ if $"Witness(a, n)"$
$quad quad quad$ return false // точно составное
return true // почти точно простое

где Witness( $a, n$ )
Пусть $t$ – количество нулей в бинарном представлении $n-1$
$u larr (n-1)//2^t$
$b larr "ModPow"(a,u,n)$
for $i in [1...t]$ do
$quad c larr b^2 mod n$
$quad$ if $c=1 and b!=1 and b!=n-1$
$quad quad quad$ return true
$quad b larr c$
if $b!=1$
$quad$ return true
return false

где ModPow( $a, b, n$ )
// $a^b mod n$ методом уменьшения задачи в 2 раза
$r larr 1$
while $b>0$
$quad$ if $b$ нечетно
$quad quad quad r larr (r*a) mod n$
$quad a larr (a*a) mod n$
$quad b larr |__b//2__|$
return $r$

В этой задаче мы получаем точное решение, но с некоторой вероятностью. Другим примером такой задачи можно считать проверку сортирующей сети, состоящей из специальных элементов:

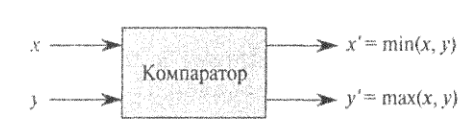
width:300px|Граф

Если сравнивающая сеть с $n$ входами правильно сортирует все $2^n$ возможных последовательностей, состоящих из нулей и единиц, то она правильно сортирует все последовательности чисел произвольного вида.

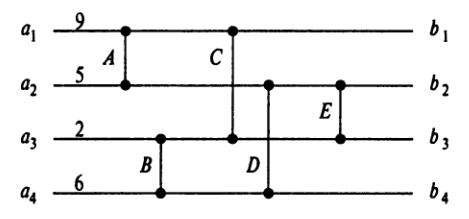
width:250px|Граф

Полное количество проверок экспоненциально. Вместо этого можно подать на вход сравнивающей сети несколько случайных тестов.

Еще одним примером вероятностного алгоритма является поиск максимального паросочетания в произвольном графе с использованием матрицы Татта.

Задания для практики

Для получение беспристрастных случайных бит от нестандартной монеты, нужно подбрасывать монету по 2 раза, пока результаты бросков не станут различными.

Алгоритм FairCoin:
do
$quad a larr$ результат броска монеты
$quad b larr$ результат броска монеты
while $a!=b$
return a

Вероятность $q$ выпадения комбинации орел-решка равна $p(1-p)$ и равна вероятности выпадения комбинации решка-орел – $(1-p)p$ .

Вероятность, что одна из двух комбинаций выпадет только на $k$ -й итерации равна $2q(1-2q)^{k-1}$ . Математическое ожидание количества итераций цикла $L=sum_{k=1}^{+oo} 2qk(1-2q)^{k-1}$ . Если $p=0.95$ , то $L=10.5$ . Но с некоторой вероятностью может быть число итераций может быть намного больше. Например, вероятность что потребуется 100 или больше итераций равна $5*10^{-5}$ . Выведите формулу и вычислите вероятность, что потребуется 1000 или более итераций.

Назад