Приближенные, рандомизированные и вероятностные алгоритмы

Для трудных задач нет полиномиальных алгоритмов, поэтому мы можем решать только экземпляры задач небольших размеров.

Но решение подобных задач может быть важно с практической точки зрения. В этом случае используют радикально иной подход к сложным оптимизационным задачам – их решают приближенно при помощи быстрого алгоритма, так как часто для практических целей достаточно хорошего, но не обязательно оптимального решения.

Хотя диапазон сложности приближенных алгоритмов весьма широк, многие из них представляют собой жадные алгоритмы, основанные на некоторой специфичной для данной предметной области эвристике. Эвристика – это основанные на здравом смысле правила, вытекающие из опыта, а не из строгих математически доказанных положений.

Если мы используем алгоритм, выходом которого является приближение настоящего оптимального решения, надо знать, насколько точным является это приближение.

Мы можем измерять точность приближенного решения `s_a` задачи минимизации некоторой функции `f` величиной относительной ошибки этого приближения
`re(s_a)=(f(s_a)-f(s^{*}))/(f(s^{*})`
где `s^{*}` – точное решение задачи.

В качестве альтернативы мы можем в качестве меры точности sa использовать отношение точности `r(s_a)=(f(s_a))//(f(s^{*})` для задачи минимизации и `r(s_a)=(f(s^{*})//(f(s_a))` для задачи максимизации.

Очевидно, что чем ближе значение `r(s_a)` к 1, тем лучшим является приближение решения.

Наилучшая (т.е. наинизшая) верхняя граница возможных значений `r(s_a)`, взятая по всем экземплярам задачи, называется коэффициентом производительности алгоритма и обозначается `R_a`. Коэффициент производительности служит в качестве основной меры, указывающей качество приближенного алгоритма.

К сожалению, некоторые простые алгоритмы имеют неограниченно большие коэффициенты производительности `R_a -> oo`. Это не означает, что такие алгоритмы нельзя использовать; надо просто быть осторожными с результатами их работы.

Приближенный алгоритм является `c`-приближенным алгоритмом, если его коэффициент производительности не превышает `c`, т.е. для любого экземпляра рассматриваемой задачи `f(s_a)<=c f(s^{*})`.

Приближенный алгоритм для решения задачи коммивояжера

В целях упрощения задачи обычно считается, что граф является полным, то есть между всеми парами вершин существует ребро. В тех случаях, когда между отдельными городами не существует сообщения, можно добавить рёбра с максимальной длиной, которые никогда не попадут в оптимальный маршрут, если он существует.

Алгоритм ближайшего соседа

Этот простой жадный алгоритм основан на эвристике ближайшего соседа: всегда идти в ближайший непосещенный город.

1. Выбрать произвольный город в качестве начального.
2. Повторять следующую операцию до тех пор, пока не будут посещены все города: идти в непосещенный город, ближайший к последнему посещенному (неоднозначности разрешаются произвольным образом).
3. Вернуться в начальный город.

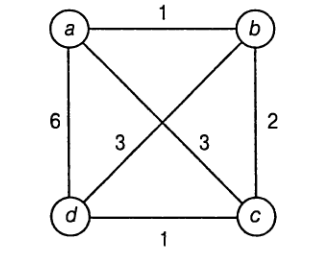Алгоритм ближайшего соседа приводит к следующему маршруту (гамильтонову циклу): `s_a : a-b-c-d-a` длиной 10. Оптимальным решением является маршрут `s^{*} : a-b-d-c-a` длиной 8. Таким образом, отношение точности этого приближения `r(s_a)=10//8=1.25`.

В общем случае нельзя ничего сказать о точности получаемых им решений, так как он может заставить нас идти по очень длинному ребру на последнем этапе пути. Мы можем изменить вес ребра `(a, d)` с 6 на произвольное сколь угодно большое число `w >= 6`, но алгоритм все равно будет давать в качестве решения маршрут `s_a : a-b-c-d-a`, длина которого равна `4 + w`. Следовательно, для этого алгоритма `R_a = oo`.

Но для важного подмножества экземпляров этой задачи, в которых выполняется два естественных условия `d[i,j]=d[j,i]` (симметрия) и `d[i,j]<=d[i,k]+d[k,j]` (неравенство треугольника), отношение точности этого алгоритма удовлетворяет неравенству `r(s_a)<=0.5(|~log_2 n~|+1)`.

Существует 1.5-приближенный алгоритм Кристофидеса решения задачи коммивояжера с евклидовыми расстояниями.

Но для произвольных графов полиномиального алгоритма с конечным `R_a` не существует, так как его можно было бы использовать для решения задачи о гамильтоновом цикле, которая также является `NP`.

Приближенные алгоритмы для задачи о рюкзаке

Жадный алгоритм

1. Вычислим удельные стоимости всех предметов множества `r_i = v_i//w_i`.
2. Отсортируем предметы в невозрастающем порядке по их удельным стоимостям, вычисленным на шаге 1 (неоднозначности разрешаются произвольным образом).
3. До тех пор пока в отсортированном списке не останется ни одного предмета, повторяем следующие действия: если текущий предмет помещается в рюкзак, мы помещаем его туда; в противном случае переходим к следующему предмету.

При помощи этого алгоритма нельзя получить гарантированную конечную верхнюю границу точности, что можно показать на следующем примере.

Емкость рюкзака `W>2`.

Алгоритм выбирает первый предмет и пропускает второй; общая стоимость подмножества равна при этом 2. Оптимальным же является выбор второго предмета стоимостью `W`. Следовательно, отношение точности `r(s_a)` этого приближенного решения равно `W//2` - величине, не ограниченной сверху.

Алгоритм очень легко модифицировать, получив 2-приближенный алгоритм. Все, что для этого нужно, – выбрать лучшее из двух решений: одно из них получается при помощи жадного алгоритма, а второе – из одного предмета наибольшей стоимости, который может поместиться в рюкзаке.

Обобщая эту идею, можно получить полиномиальный алгоритм с эффективностью `O(n^{k+1})` и `R_a=1+1/k`, где `k<n`. Алгоритм генерирует все подмножества из `k` или меньшего количества предметов и для каждого из подмножеств, которое помещается в рюкзак, добавляет оставшиеся предметы жадным способом (т.е. в невозрастающем порядке их удельных стоимостей).

Задания для практики

1. К какому классу временной эффективности принадлежит жадный алгоритм для решения задачи о рюкзаке?
2. Разработайте жадный алгоритм с полиномиальным временем работы для задачи о раскраске графа.
3. Есть `N` шаров, из них `M` (`1<=M<=N`) шаров радиоактивные. В детектор можно загрузить от 1 до `N` шаров. Детектор подает сигнал, если среди них окажется `K` (`1<=K<=M`) или более радиоактивных. Необходимо найти радиоактивные шары, сделав как можно меньше испытаний.