 Классы сложности задач. Методы решения трудных задач
Классы сложности задач. Методы решения трудных задач
Классы сложности задач Сравнение методов решения трудных задач Метод поиска с возвратом Метод ветвей и границ
 Метод ветвей и границ
Метод ветвей и границ
задачи, как только можно сделать вывод, что она не ведет к решению. Эта идея
может быть усилена при работе с оптимизационными задачами, которые
должны минимизировать или максимизировать целевую функцию, обычно при
наличии некоторых ограничений.
*Допустимое решение* удовлетворяет всем ограничениям задачи
(например, гамильтонов цикл в задаче коммивояжера), в то время как *оптимальное
решение* является допустимым решением с наилучшим
значением целевой функции (например, кратчайший гамильтонов цикл).
--
По сравнению с методом поиска с возвратом метод ветвей и границ требует:
* способа получить для каждого узла дерева пространства состояний
границу наилучшего значения целевой функции для всех решений,
которые могут быть получены путем дальнейшего добавления
компонентов к частичному решению, представленному узлом;
* значение наилучшего решения, полученного к этому моменту.
--
Если такая информация доступна, мы можем сравнивать значение границы
узла со значением наилучшего решения, полученного к этому моменту: если
значение границы не лучше значения уже имеющегося наилучшего решения —
т.е. не меньше в случае задачи минимизации или не больше в случае задачи
максимизации, — то такой узел является бесперспективным и его обработка может быть
завершена, поскольку ни одно получаемое из него решение не может оказаться лучше того,
что уже имеется. В этом заключается основная идея метода ветвей и границ.
Также ветвь обрезается из-за нарушений ограничений, как в поиске с возвратом.
При достижении допустимого решения мы сравниваем значение целевой функции для этого
решения со значением целевой функции наилучшего
полученного к настоящему моменту решения и обновляем последнее
текущим, если новое решение оказывается лучше.
--
##### Задача о назначениях
В задаче о назначениях имеется `n` работников, которым надо выполнить `n` заданий, и надо найти
распределение заданий по работникам с наименьшей общей стоимостью.
В терминах матрицы стоимости `C` в задаче требуется
выбрать по одному элементу из каждой строки матрицы так, чтобы выбранные
элементы находились в разных столбцах, а их общая сумма имела наименьшее
возможное значение.

--
Стоимость любого решения, включая оптимальное, не может быть меньше суммы
наименьших элементов в каждой из строк матрицы. Для приведенного
примера эта сумма равна `2 + 3 + 1 + 4= 10`.
Мы можем применять такие же рассуждения и к частично построенным решениям. Например, для любого
допустимого решения, которое выбирает из первой строки 9, нижняя граница `lb` равна
`9 + 3 + 1 + 4 = 17`.
--
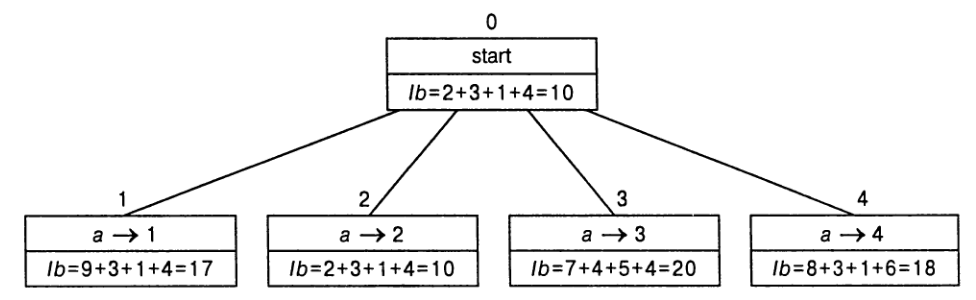
Значение нижней границы `lb` для корня равно 10. Узлы на первом уровне
дерева соответствуют четырем элементам (заданиям) в первой строке матрицы,
поскольку все они могут быть потенциальными первыми компонентами решения.
Наиболее обещающим среди них является узел 2,
поскольку он имеет наименьшее значение нижней границы. Следуя стратегии
выбора наилучшего варианта, исследуем сперва эту ветвь, перед тем как перейти
к остальным.
--
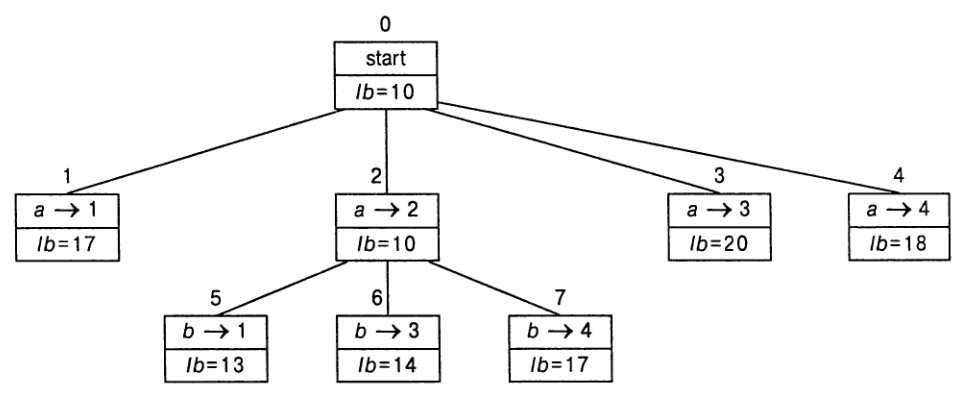
Из рассматриваемого листа выходят три ветви, соответствующие
выбору элемента из второй строки, не находящегося во втором столбце, и
представляющие три различные задания, назначенные работнику `b`.
--
Из шести листьев (узлы 1, 3, 4, 5, 6 и 7), которые могут содержать
оптимальное решение, мы вновь выбираем лист с наименьшим значением нижней
границы, а именно — узел 5. Сначала рассмотрим выбор третьего элемента из строки `c` —
при этом у нас не остается иного выбора, кроме назначения задания 4 работнику `d`, что дает нам лист 8.
--
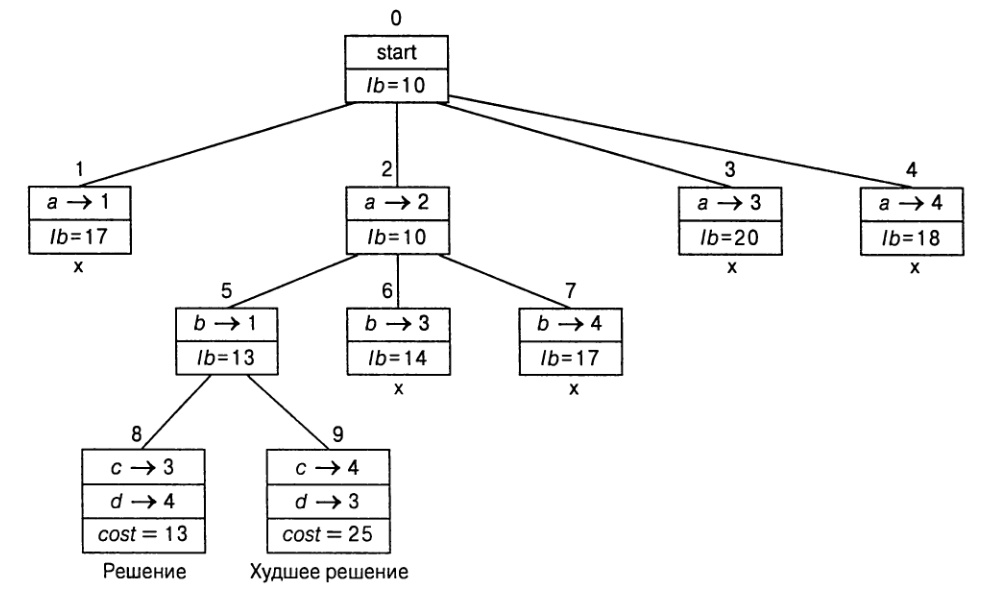
Лист 8 соответствует допустимому решению `{a -> 2, b -> 1, c -> 3 ,d -> 4}` с
общей стоимостью 13. Узел 9 соответствует допустимому решению
`{a -> 2, b -> 1, c -> 4 ,d -> 3}` с большей стоимостью 25.
Далее, если мы обратимся к каждому из пяти листьев последнего дерева
пространства состояний (узлы 1, 3, 4, 6 и 7 на рис. 11.7), то обнаружим, что
их значения нижних границ не меньше значения целевой функции наилучшего
решения, обнаруженного к настоящему времени (равного 13, в листе 8).
Следовательно, работа с ними прекращается, и решение, представленное листом 8,
является оптимальным решением поставленной задачи.
--
##### Задача о рюкзаке
Дано `n` предметов с весами `w_1,...,w_n` (возможно не целыми!) и ценами `v_1,..., v_n`, а также рюкзак, выдерживающий вес `W`.
Требуется найти подмножество предметов, которое можно разместить в рюкзаке
и которое имеет при этом максимальную цену.
Оказывается удобным упорядочить предметы в убывающем порядке по их удельной цене:
`v_1/w_1 >= v_2 / w_2 >= ... >= v_n/ w_n`
--
Дерево пространства состояний для данной задачи
является бинарным деревом, каждый
узел на уровне `0 <= i <=n` представляет все подмножества из `n` элементов.
Этот выбор однозначно определяется путем от корня к узлу: ветвь, идущая
влево, указывает на включение очередного элемента в подмножество, в то время
как правая ветвь указывает на отсутствие элемента в подмножестве.
Запишем общий вес `w` и общую стоимость `v` выбора, соответствующего узлу, вместе
с верхней границей `ub` значения для любого подмножества, которое может быть
получено путем добавления некоторых элементов (возможно, никаких) к этому
выбору.
--

--
Простым способом вычисления верхней границы `ub` является добавление к
общей стоимости уже выбранных элементов v произведения оставшейся емкости
рюкзака `W - w` и наибольшего значения удельной стоимости среди оставшихся
элементов, которое равно `v_{i+i}//w_{i+1}`:
`ub = v + (W - w) v_{i+i}//w_{i+1}`.
Пусть `W=10`
Предмет|Вес|Стоимость|Удельная стоимость
--|--|--|--
1 |4 |40|10
2 |7 |42|6
3 |5 |25|5
4 |3 |12|4
--
В корне дерева пространства состояний не выбран ни один элемент.
Следовательно, как общий вес, так и общая стоимость выбранных элементов равны 0.
Значение верхней границы, вычисленное по формуле, равно 100.
Узел 1, левый дочерний узел корня, представляет подмножество, состоящее из одного
предмета, 1; общий вес и стоимость в этом узле равны, соответственно, 4 и 40,
а значение верхней границы — `40 + (10 -4) -6 = 76`.
Узел 2 представляет подмножество, которое не включает предмет 1, так что в этом узле `w =0`, `v = 0`
и `ub = 0 + (10 -0) *6 = 60`.
Поскольку узел 1 имеет большую верхнюю границу, чем узел 2, он является
более перспективным для данной задачи максимизации, и мы
начинаем ветвление с узла 1.
--
Его дочерние узлы — 3 и 4 — представляют подмножества с элементом 1 и с и без элемента 2, соответственно.
Поскольку общий вес любого подмножества, представленного узлом 3, превосходит емкость рюкзака,
работа с этим узлом завершается.
У узла 4 те же значения общего веса и общей
стоимости, что и у родительского, так что значение верхней границы у этого узла
`ub = 40+(10 -4)*5 = 70`.
Из узлов 2 и 4 для дальнейшего ветвления мы выбираем узел 4 и получаем узлы 5 и 6,
включающий и не включающий, соответственно, предмет 3.
Ветвление из узла 5 дает узел 7, который дает недопустимое решение, и узел 8, представляющий подмножество
`{1,3}`.
Оставшиеся узлы 2 и 6 имеют меньшие значения верхней границы, чем решение,
представленное узлом 8. Следовательно, работа с этими узлами завершается, и множество
`{1,3}` из узла 8 является оптимальным решением задачи.
--
Поиск хорошей функции для вычисления границ -- задача обычно
непростая. С одной стороны, требуется, чтобы эта функция была легко вычислимой.
С другой, она не может быть слишком упрощенной -- в противном случае она не
сможет выполнять свою основную задачу отсечения как можно большего
количества ветвей дерева пространства состояний. Поиск компромисса между этими
конкурирующими требованиями может потребовать интенсивных экспериментов
с широким диапазоном экземпляров рассматриваемой задачи.
---
##### Задания для практики
1. Герой одним выстрелом из BFG может уничтожить врага и двух его соседей, стоящих рядом (после выстрела в ряду врагов образуется пустое место). Затем враги стреляют в него, нанося ущерб `D_i` (`D={4,6,1,12,3,5,5,5}`). Определите наименьший суммарный ущерб, который могут нанести враги герою, пока герой не уничтожит всех врагов.

 Начало
Начало Учебные материалы
Учебные материалы