Начало
Учебные материалы
Классы сложности задач. Методы решения трудных задач
Классы сложности задач Сравнение методов решения трудных задач Метод поиска с возвратом Метод ветвей и границ
Метод поиска с возвратом
Задача заключается в размещении `n` ферзей на
шахматной доске размером `n x n` так, чтобы никакие два ферзя не угрожали друг другу,
находясь на одной горизонтали, вертикали или диагонали. Для `n = 1` задача
имеет тривиальное решение; легко убедиться, что для `n = 2` и `n = 3` решений не
существует.
 Решим задачу для `n=4` с помощью поиска с возвратом.
Поскольку каждый ферзь должен находиться на собственной горизонтали, все, что надо, — это указать вертикаль для каждого ферзя на доске.
--
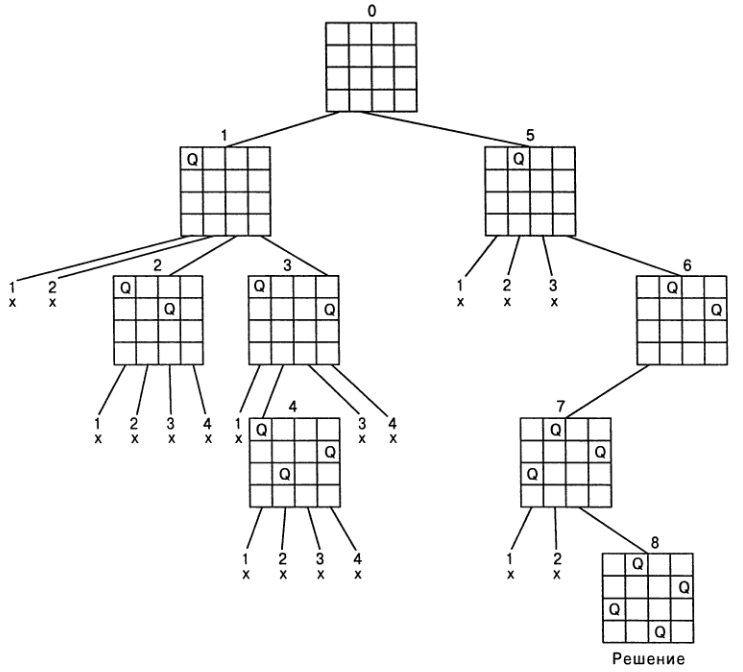
Начинаем с пустой доски и помещаем ферзя 1 в первую возможную позицию
на его горизонтали; это позиция на вертикали 1. Затем мы размещаем ферзя 2
в первую допустимую позицию (после неудачных попыток размещения на
вертикалях 1 и 2) на вертикали 3, в квадрате (2,3). Это тупиковая позиция, поскольку
при ней оказывается невозможно разместить третьего ферзя так, чтобы он не
был под боем. Соответственно, алгоритм осуществляет возврат к предыдущему
состоянию и помещает ферзя в позицию (2,4). После этого третий ферзь может
быть помещен только в позицию (3,2), что приводит к очередному тупику После
этого алгоритм осуществляет возврат к ферзю 1 и помещает его в очередной
допустимой позиции (1,2). Ферзь 2 может быть размещен только в позиции (2,4),
ферзь 3 — только в позиции (3,1), а ферзь 4 — в позиции (4,3), что дает
решение поставленной задачи.
--
--
##### Задача о гамильтоновом цикле
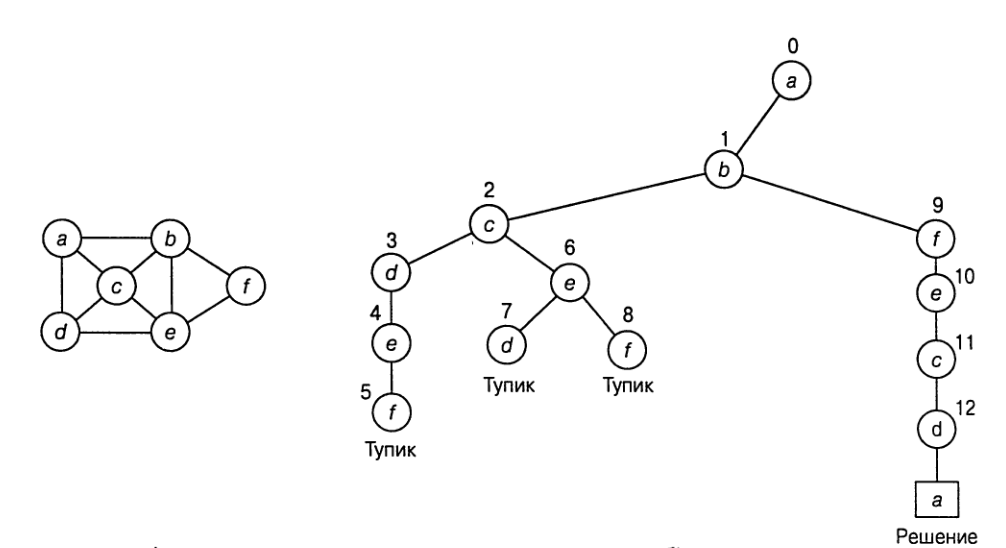
Без потери общности можно считать, что если гамильтонов цикл существует,
то он начинается в вершине `a`. Соответственно, мы делаем вершину `a` корнем
дерева пространства состояний. Используя алфавитный порядок для разрешения
неоднозначности при выборе вершин, смежных с вершиной `a`, мы выбираем вершину `b`.
После вершины `b` алгоритм обращается к вершинам `c`, `d`, `e` и, наконец, к `f`, которая
является тупиком.
Соответственно алгоритм возвращается к вершине `c` —
первой вершине, которая позволяет получить отличное от рассмотренного решение.
Переход от `c` к `e` не приводит к решению, и алгоритм должен вернуться к вершине
`b`. Из вершины `b` мы попадаем в вершину `f`, а за ней —
в вершины `e`, `c` и `d`, из которой можно вполне законным путем вернуться в `a`, что
дает гамильтонов цикл `a-b-f-e-c-d-a`. Если мы хотим найти еще какой-то гамильтонов цикл, то можем
продолжить процесс возврата из листа, соответствующего найденному решению.
--
--
##### Задача о подмножестве с заданной суммой
Требуется найти подмножество данного множества `S = {s_1,...,s_n}`, состоящего из `n` натуральных чисел,
такое, что сумма его элементов равна заданному натуральному числу `d`. Например,
для `S = {1,2,5,6,8}` и `d = 9` имеется два решения — {1,2,6} и {1,8}.
Удобно отсортировать элементы множества в возрастающем порядке. Будем
считать, что `s_1<=s_2<=...<=s_n`.
--
Дерево пространства состояний может быть построено как бинарное дерево.
Корень дерева представляет начальную точку, в которой не принято решение ни по одному из
элементов множества. Его левый и правый дочерние узлы представляют,
соответственно, включение `s_1` в искомое подмножество и отсутствие в нем этого элемента.
Аналогично, переход влево от узла на первом уровне означает включение `s_2` в
искомое подмножество, а переход вправо — отсутствие этого элемента в искомом
множестве. Таким образом, путь от корня к узлу на `i`-ом уровне дерева указывает,
какие из первых `i` чисел будут включены в подмножество, представленное этим
узлом.
--
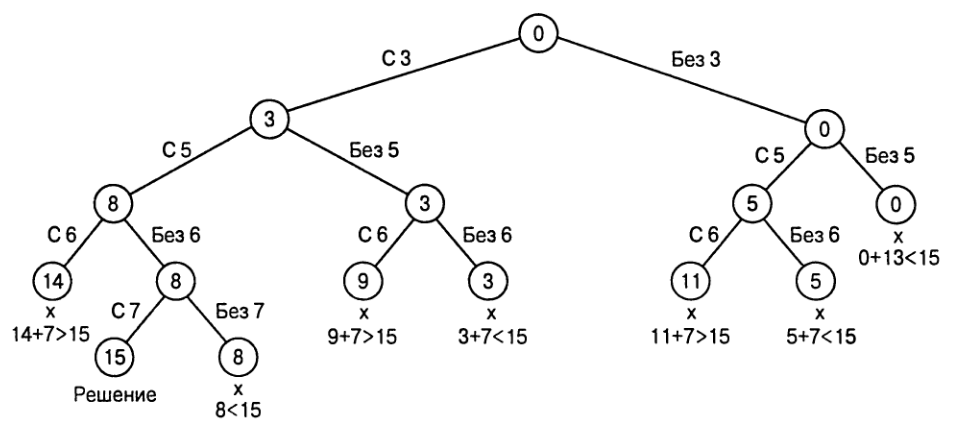
Полное дерево пространства состояний (для поиска *всех* решений).
--
Запишем значение `r` суммы этих чисел, в узле. Если `r` равно `d`, мы
получаем решение поставленной задачи. Мы можем либо сообщить о нем и
прекратить работу алгоритма, либо, если надо найти все решения, выполнить
очередной возврат к родительскому узлу и продолжить работу.
Если `r` не равно `d`, мы можем завершить работу с узлом как с бесперспективным при выполнении
любого из двух условий:
`r+s_{i+1}>d` (сумма слишком велика)
`r + sum_{j=i+1}^n s_j < d` (сумма слишком мала)
--
Поиск с возратом применяется для сложных комбинаторных
задач, для точного решения которых не существует эффективных
алгоритмов.
В отличие от исчерпывающего поиска, который чрезвычайно
медленно работает для всех экземпляров задачи, поиск с возвратом как минимум
оставляет надежду на то, что решение некоторых экземпляров нетривиальных
размеров будет найдено за приемлемое время.
Даже если поиск с возвратом не удаляет ни одного элемента из пространства состояний
задачи и в результате генерирует все его элементы, то он все равно обеспечивает
удобный способ генерации, который может быть ценен сам по себе.
---
##### Задания для практики
1. а) Примените поиск с возвратом для решения следующего экземпляра задачи о сумме подмножества: `S ={1,3,4,5}` и `d = 11`.\
б) Будет ли алгоритм поиска с возвратом корректно работать при использовании только одного из двух неравенств для завершения обработки узла как бесперспективного?
2. Получить все представления натурального числа `N=10` суммой натуральных чисел. Перестановка слагаемых нового способа представления не даёт.
