Подразделы

Другие разделы

Дата и время

04/04/2025 10:50:07

Авторизация

Пространственно-временной компромисс

Идея пространственно-временного компромисса Массив частичных сумм Сортировка подсчетом Хеширование Вычисление биномиальных коэффициентов Задача о рюкзаке

Задача о рюкзаке

Даны $n$ предметов с известными весами $w_1,..., w_n$ и стоимостями $v_1,..., v_n$ и рюкзак вместимостью $W$ . Требуется найти наиболее ценное подмножество предметов, помещающееся в рюкзаке. Все веса и емкость рюкзака представляют собой положительные целые числа; стоимости предметов — не обязательно целые числа.

Для разработки алгоритма динамического программирования мы должны вывести рекуррентное соотношение, которое выражает решение экземпляра задачи о рюкзаке через решения его меньших подэкземпляров. Рассмотрим экземпляр, определяемый первыми $i$ предметами ( $1 <= i <= n$ ), и емкостью рюкзака $j$ ( $1 <= j <= W$ ). Пусть $V[i, j]$ — значение оптимального решения этого экземпляра, т.е. стоимость наиболее ценного подмножества из первых $i$ предметов, которое помещается в рюкзак емкостью $j$ .

Мы можем разделить все подмножества первых $i$ предметов, которые помещаются в рюкзак емкостью $j$ , на две категории: те, которые не включают $i$ -ый предмет, и те, которые его включают.

Среди подмножеств, которые не включают $i$ -ый предмет, стоимость оптимального подмножества по определению равна $V[i-1, j]$ .
Среди подмножеств, которые включают i-ый предмет (следовательно, $j - w_i>= 0$ ), оптимальное подмножество составляется из этого предмета и оптимального подмножества первых $i-1$ предметов, которое размещается в рюкзаке емкостью $j -w_i$ . Стоимость такого оптимального подмножества равна $v_i + V [i-1, j -w_i]$ .

Cтоимость оптимального решения среди всех допустимых подмножеств из первых $i$ предметов представляет собой большее из этих двух значений.

Это к следующему рекуррентному соотношению:

$V[i,j]={(max(V[i-1, j],v_i + V [i-1, j -w_i])," при "j - w_i>= 0),(V[i-1, j]," при "j - w_i< 0):}$

Начальные условия определяем следующим образом:

$V[0,j]=0$ при $j>=0$ , $V[i,0]=0$ при $i>=0$ .

Нужно найти $V[n, W]$ .

Пример решения

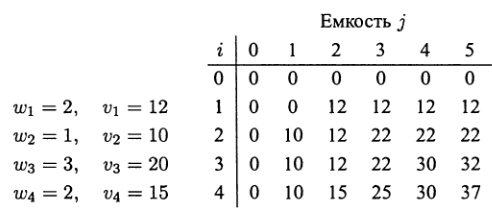
width:400px|

Максимальная стоимость $V [4,5] = 37$ .

Мы можем найти состав оптимального подмножества, отслеживая вычисления этого элемента таблицы. Поскольку $V [4,5] != V [3,5]$ , предмет 4 был включен в оптимальное решение вместе с оптимальным подмножеством, заполняющим оставшиеся $5 -2 = 3$ единицы емкости рюкзака. Последние представлены элементом $V [3,3]$ . Поскольку $V [3,3] = V [2,3]$ , элемент 3 не является частью оптимального подмножества. Далее, так как $V[2,3] != V [1,3]$ , предмет 2 также является частью оптимального выбора, после чего элемент $V[1,2]$ остается в качестве определения оставшейся части подмножества. Аналогично, так как $V [1,2] != V [0,2]$ , делаем вывод, что предмет 1 является последней частью оптимального решения, которое представляет собой множество ${1, 2, 4}$ .

Как временная, так и пространственная эффективность данного алгоритма равна $Theta(nW)$ . Время, требующееся для поиска состава оптимального подмножества, равно $Theta(n + W)$ .

Мы можем заполнять таблицу либо сверху вниз (рекурсивно, с помощью запоминающей функции), либо снизу вверх (без использования рекурсии).

Задания для практики

Разработайте алгоритм динамического программирования для задачи о размене: дана величина $S$ и неограниченное количество монет достоинством $d_1, ..., d_m$ . Требуется найти наименьшее количество монет, которые в сумме дают величину $S$ , или указать, что задача не имеет решения.