Подразделы

Другие разделы

Дата и время

04/04/2025 10:26:06

Авторизация

Пространственно-временной компромисс

Идея пространственно-временного компромисса Массив частичных сумм Сортировка подсчетом Хеширование Вычисление биномиальных коэффициентов Задача о рюкзаке

Хеширование

Теперь рассмотрим очень эффективный способ реализации словарей, позволяющих хранить пары вида (ключ, значение). К основным операциям над словарем относятся: добавления пары, поиска и удаления пары по ключу.

Для реализации словарей можно использовать массивы или связные списки и двоичные деревья поиска.

Хеширование основано на идее распределения ключей в одномерном массива $H[0...m-1]$ , называющемся хеш-таблицей. Хеш-функция $h$ назначает каждому из ключей хеш-адрес, который представляет собой целое число от 0 до $m-1$ . Каждая ячейка содержит связный список пар, у которых ключи получили хеш-адрес, соответствующий данной ячейке. Таким образом, все операции со словарем будут выполняться только в небольшом списке пар с совпадающим хеш-адресом.

Хеш-функция должна удовлетворять двум требованиям:

она должна распределять ключи по ячейкам хеш-таблицы как можно более равномерно (для этого $m$ выбирается простым);
она должна легко вычисляться.

Например, если ключи представляют собой неотрицательные целые числа, то хеш-функция может иметь вид $h(K) = K mod m$ . Если ключи — символы некоторого алфавита, то можно применить к номеру символу $"ord"(K)$ в алфавите ту же функцию, что и для целых чисел.

Если $K$ — символьная строка $c_0 c_1... c_{n-1}$ , можно вычислить $h(K)$ по формуле:
$h larr 0$
for $i in [0..n-1]$
$quad h larr (h*P+"ord"(c_i)) mod m$
где $P$ – константа, обычно некоторое простое число.

width:700px|Пример

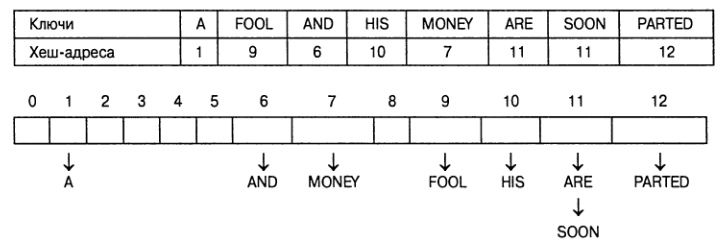
Для упрощения здесь $P=1$
$h(ARE) = (1 + 18 + 5) mod 13 = 11$
$h(SOON) = (19 + 15 + 15 + 14) mod 13 =11$

Если мы хотим найти хеш-таблице слово KID, то должны начать с вычисления для него хеш-функции: $h(KID) = 11$ . Поскольку список, присоединенный к ячейке 11, не пуст, мы должны просмотреть ключи в этом списке. После сравнения слова KID сначала со словом ARE, а затем со словом SOON мы убеждаемся, что искомого слова в таблице нет.

Выбрав размер хеш-таблицы $m$ меньшим, чем количество ключей $n$ , мы обречены на коллизии — ситуации, когда два или более ключей хешируются в одну и ту же ячейку хеш-таблицы. Но коллизий следует ожидать, даже если $m$ значительно больше $n$ . В наихудшем случае все ключи могут быть хешированы в одну ячейку хеш-таблицы. К счастью, при соответствующем выборе размера хеш-таблицы и хорошей хеш-функции такая ситуация встречается очень редко.

Эффективность поиска зависит от длины связных списков, которая, в свою очередь, зависит от размеров $m$ хеш-таблицы и качества хеш-функции. Если хеш-функция распределяет $n$ ключей по $m$ ячейкам практически равномерно, то в каждом списке будет содержаться примерно около $n//m$ пар.

Cреднее количество сравнений для последовательного поиска равно
$C_{"avg"} (n)=p/2+n-(p*n)/2 in Theta(n)$ ,
где $n$ – длина списка, $p$ – вероятность наличия ключа в списке.

При помощи хеширования мы достигаем снижения среднего размера связного списка в $m$ раз. Так как $m>n$ , то $C_{"avg"} (n//m) in Theta(1)$ , что лучше эффективности $Theta(log n)$ для двоичных деревьев поиска.

Такая эффективность получена ценой излишнего потребления памяти – многие ячейки хэш-таблицы остаются пустыми.

Задания для практики

Для входных данных 30, 20, 56, 75, 31, 19 и хеш-функции $h(K) == К mod 11$
а) постройте хеш-таблицу;
б) найдите наибольшее количество сравнений ключей при успешном поиске в полученной таблице;
в) найдите среднее количество сравнений ключей при успешном поиске в полученной таблице.