 Вычислительные основы
Вычислительные основы
Реальные компьютеры vs. модели вычислений Детерминированный конечный автомат Машина Тьюринга Нормальный алгоритм Маркова Теория рекурсивных функций * Практическое использование
 Реальные компьютеры vs. модели вычислений
Реальные компьютеры vs. модели вычислений
функций по аппроксимирующим полиномам до шестой степени методом конечных разностей. Эта машина использовала десятичную систему счисления и выполняла вычисления с точностью 18 знаков.
К сожалению, изобретатель не смог при своей жизни построить полностью работающую версию задуманной им машины. Во второй половине 19-го века
другие изобретатели по его чертежам сумели построить работающие версии разностных машин, одна из которых даже использовалась для расчёта и публикации логарифмических таблиц.
В 1835 году Бэббидж разработал общую версию механического компьютера - «аналитическую машину», которую построили в конце 20 века для Лондонского музея науки.

--
В Турине Бэббидж познакомился с итальянским инженером Менабреа и вдохновил его
написать обзор возможностей аналитической машины. В 1842 Менабреа опубликовал работу по этой теме на французском языке. Ада Лавлейс перевела её на английский и добавила свои примечания.
В примечании А к фразе Менабреа, что эта машина является инструментом для автоматизации «длительных и скучных вычислений», Ада
написала, что машина не будет ограничена работой с числами, и может обрабатывать любые объекты,
«чьё взаимное фундаментальное взаимодействие можно выразить абстрактной наукой операций, и которые можно приспособить к операционным записям и механизму машины»
и когда-нибудь такая машина сможет сочинять музыку.
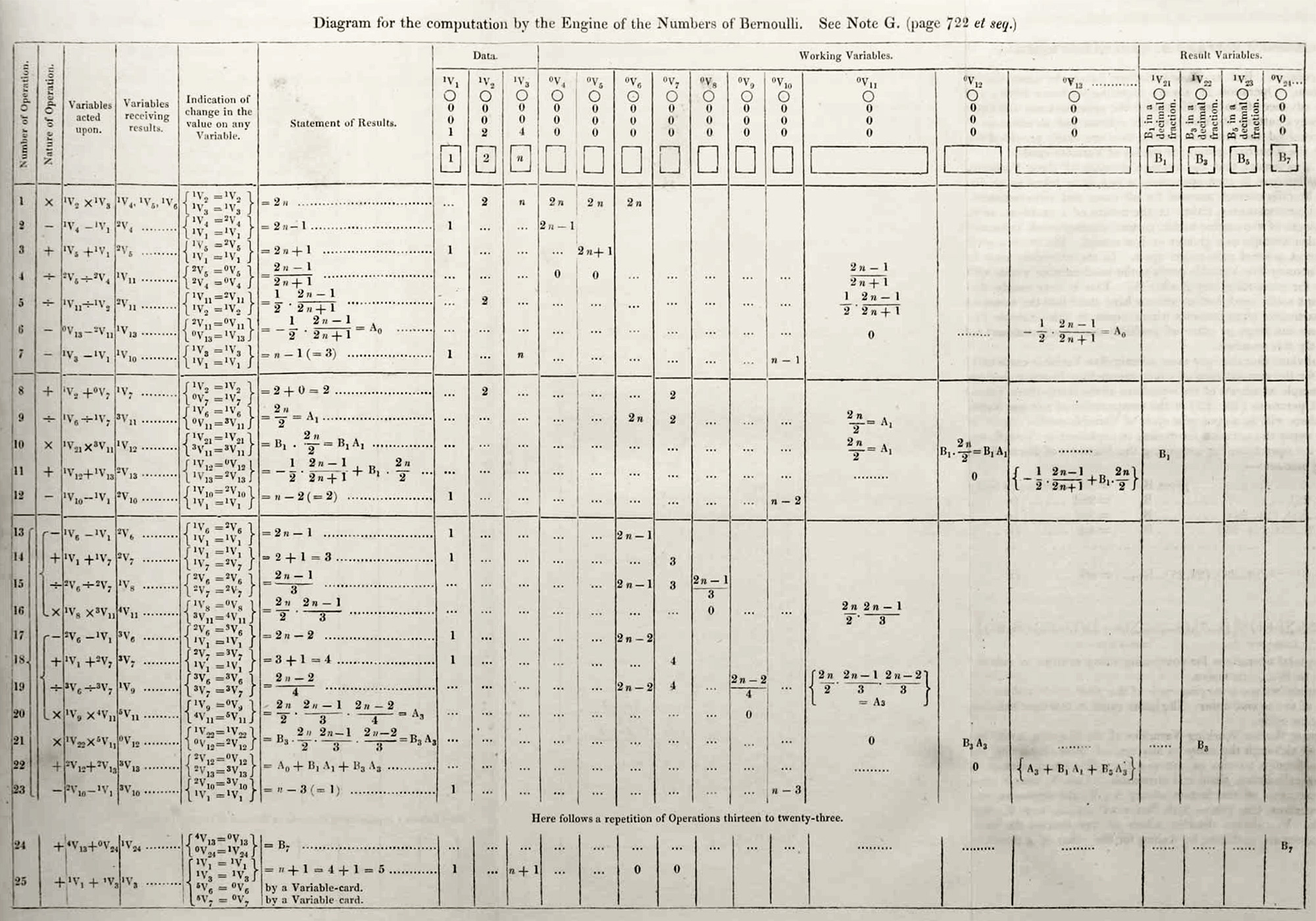
В примечании G, Ада Лавлейс пишет, что, несмотря на впечатляющие возможности, нельзя сказать, что аналитическая машина «думает».
Тем не менее машина способна на удивительные вещи и в качестве примера записывает программу для вычисления чисел Бернулли.
--
Первым компьютером, управляемым программой, стал Z3, построенный Цузе в 1941 году.

Он работал на электрических реле, в дальнейшем компьютеры использовали электровакуумные лампы, транзисторы, микросхемы и т.д.
Современные компьютеры используют архитектуру, предложенную фон Нейманом:
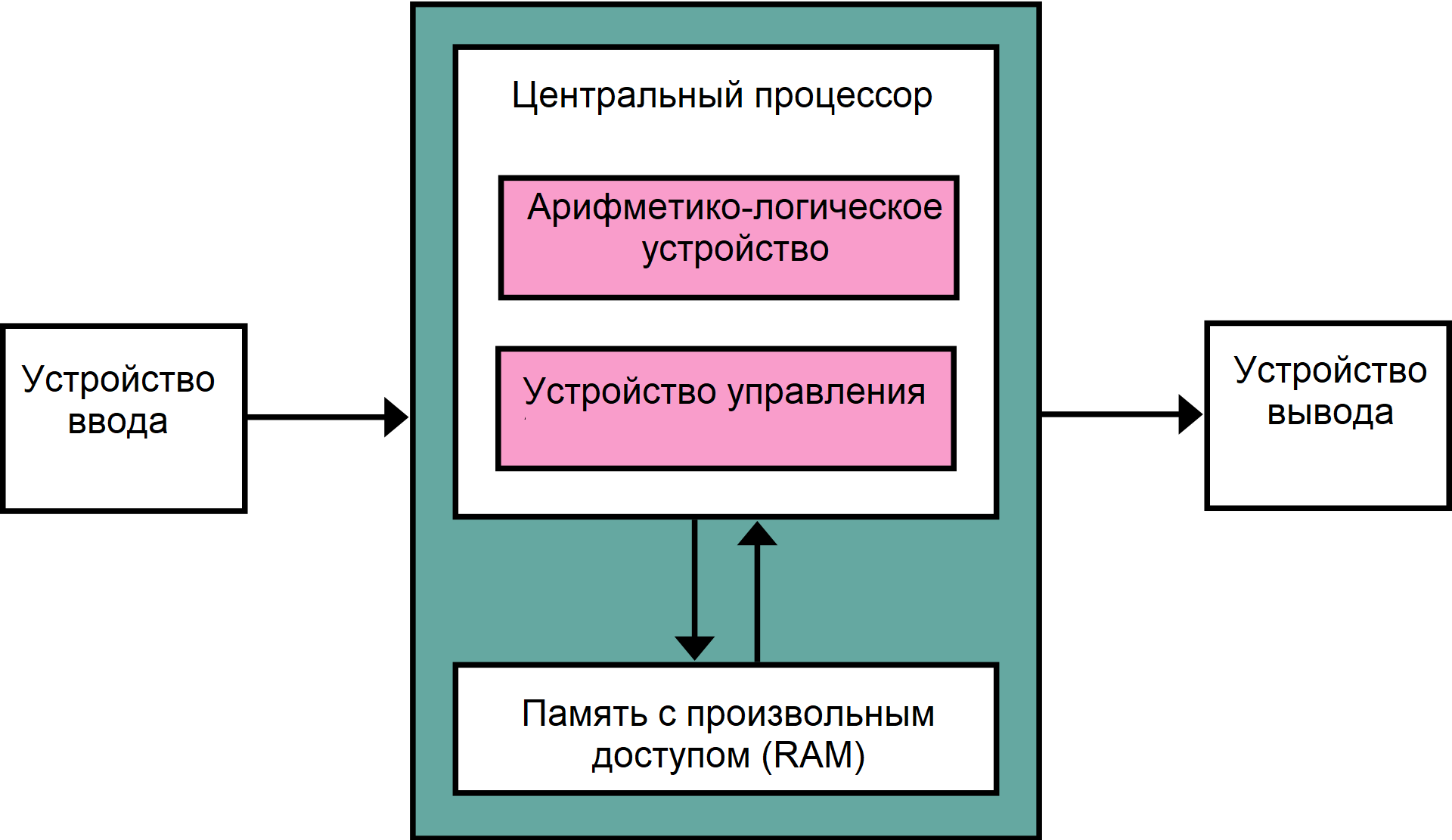
1. Команды и данные хранятся в одной и той же памяти и неразличимы.
Одно и то же значение в ячейке памяти может использоваться и как данные, и как команда в зависимости от способа обращения к нему.
(В Гарвардской архитектуре память команд и данных разделены)
2. Память состоит из пронумерованных ячеек, причём процессору в произвольный момент доступна любая ячейка.
3. Все вычисления, предусмотренные алгоритмом решения задачи, должны быть представлены в виде программы,
состоящей из последовательности команд, которые выполняются специальным устройством, называемым центральным процессором.
В каждый момент времени выполняется только одна команда. Команды выполняются последовательно, но с помощью специальных команд порядок выполнения может быть изменен.
---
Следует различать
- описание алгоритма (программа)
- механизм реализации алгоритма (средства реализации элементарных шагов, запуска и останова, ввода и выдачи результата, обеспечения детерминированности)
- процесс выполнения на конкретных данных
--
Рассмотренные ранее способы описания алгоритма отражают только связи по управлению, но не содержат сведений о данных, памяти и наборе элементарных шагов.
Поэтому необходима *модель вычислений*, которая включает в себя
- конечный набор элементарных объектов;
- конечный набор способов построения из них новых объектов;
- набор элементарных действий;
- способ сохранения и выборки информации из памяти
--
Можно выделить три основных типа моделей вычислений
1. Через механизм рекуррентных определений (рекурсивные функции, лямбда-исчисление)
2. Через определение детерминированного устройства, выполняющего набор элементарных операций (машина Тьюринга, машина Поста, любой компьютер).
3. Через замену части слова другим подсловом (конечные автоматы, нормальный алгоритм)
--
Все эти модели необходимы для формализации понятия вычислимости. Так как в современном процессоре слишком много "элементарных" операций,
то для математических доказательств ранее рассмотренных свойств алгоритма применяется более простые модели. Математиками была
доказана возможность переписывания программы для любой модели в эквивалентную программу для другой модели. При появлении
нового вычислительного устройства достаточно доказать возможность имитации на нём машины Тьюринга, тогда этот исполнитель может вычислить любую вычислимую по Тьюрингу функцию.
С другой стороны было доказано, что машина Тьюринга может имитировать любое вычислительное устройство.

 Начало
Начало Учебные материалы
Учебные материалы