Подразделы

Другие разделы

Дата и время

09/04/2025 22:13:36

Авторизация

Вычислительные основы

Реальные компьютеры vs. модели вычислений Детерминированный конечный автомат Машина Тьюринга Нормальный алгоритм Маркова Теория рекурсивных функций * Практическое использование

Детерминированный конечный автомат

Детерминированный конечный автомат (ДКА, deterministic finite automaton, DFA) – это модель вычисления, заданная кортежем $A = (Sigma, Q, q_0, delta, F)$ , где:

$Sigma$ – алфавит, то есть конечное множество входных символов;
$Q$ – конечное множество состояний;
$q_0 in Q$ – начальное состояние;
$delta: Q xx Sigma -> Q$ – функция перехода, то есть «программа», которая исполняет детерминированный конечный автомат. $delta$ вычисляет следующее состояние $p = delta(q, a)$ , где $p, q in Q, a in Sigma$ ;
$F sube Q$ – множество финальных состояний (для автомата-распознавателя)

Для автомата-преобразователя вместо $F$ нужно задать функцию выхода $lambda: Q -> Phi$ (автомат Мура) или $lambda: Q xx Sigma -> Phi$ (автомат Мили), где $Phi$ - множество выходных символов.

Для того чтобы увидеть, что ДКА, заданный $А$ , принимает строку $w$ , мы «выполняем» $А$ на $w = a_1 a_2 ... a_n$ следующим образом: $delta(q_0, a_1) = q_1$ , $delta(q_1, a_2) = q_2$ … $delta(q_{n-1}, a_n) = q_n$ . $A$ принимает $w$ тогда и только тогда, когда $q_n in F$ , то есть если $q_n$ является одним из финальных (принимающих) состояний. В противном случае мы говорим, что ДКА отклоняет $w$ .

Предположим, что мы хотим спроектировать детерминированный конечный автомат для языка L01, в котором допустимы только цепочки символов, содержащие 01. Пусть $Sigma = {0, 1}$ , $Q = {q_0, q_1, q_2}$ и $F = {q_1}$ . Существует два способа представить $delta$ : в форме диаграммы переходов либо в форме таблицы переходов.

_	0	1
$q_0$	$q_2$	$q_0$
$q_1$	$q_1$	$q_1$
$q_2$	$q_2$	$q_1$

Недетерминированный конечный автомат (НКА, nondeterministic finite automaton, NFA) определяется аналогично ДКА, за исключением того, что переходная функция $delta$ становится переходным отношением, то есть $delta in Q xx Sigma xx Q$ , то есть на одной и той же паре $(q, a)$ может существовать более одного возможного нового состояния (или ни одного). Также мы можем смотреть на $delta$ как на $delta : Q xx Sigma -> P(Q)$ , где $P(Q)$ – это множество подмножеств $Q$ .

НДКА для языка Ln - $n$ -ый символ с конца равен 1.

Теорема Детерминированный и недетерминированный конечные автоматы являются эквивалентными.

Очевидно, что ДКА – это особый случай НКА. Таким образом, остается доказать, что каждый НКА может быть перепроектирован как ДКА, что осуществляется через построение подмножеств.

Сначала мы принимаем допущение, что НКА $N$ не имеет $varepsilon$ -переходов. Пусть $M$ это ДКА, и тогда $Q_M = P(Q_N)$ , где $P(Q_N)$ – состоит из всех возможных подмножеств множеств $Q_N$ , и $delta_M(Q, a) := bigcup_{q in Q} delta_N(q, a)$ , где $Q in P(Q_N)$ .

Также $F_M = {Q in P(Q_N) : Q cap F_N != emptyset}$ и $(q_M)_0 := {(q_N)_0}$ .

Если $N$ имеет $varepsilon$ -переходы, то $delta_M(Q, a) := bigcup_{q in Q} varepsilon-closure(delta_N(q, a))$ .

Отметим, что происходит экспоненциальный рост состояний, поскольку $|P(Q_N)| = 2^{|QN|}$ . Мы симулируем более выразительную модель вычисления (НКА) с помощью более ограниченной (ДКА).

Рассмотрим пример преобразования из НКА для L2 (L2 – это множество строк, где предпоследний символ равен 0) в ДКА.

ДКА для L2 (7 состояний справа недостижимы, их можно убрать)

Описанный КА использует только одну ячейку памяти, в которой хранится текущее состояние и может только распознавать или преобразовывать цепочки символов. Если добавить в КА возможность использовать память и выполнять действия, то можно описать любое вычислительное устройство (компьютер). В функцию перехода добавляются параметры, связанные с текущим состоянием памяти, а результат включает не только изменение состояния, но и изменение памяти. Для диаграмм, описывающих КА общего вида, используется, например, UML.

width:400px|телефон

Различают конечные автоматы

с конечной памятью (можно свести к КА без памяти, включив состояние памяти в номер состояния, что существенно усложняет определение КА);
с бесконечной памятью (рассматривают обычно КА с памятью организованной в форме стека, такие КА используются в компиляторах).

Объекты в ООП рассматриваются как КА с памятью.

Задания для практики

Формат числа описывается следующей схемой

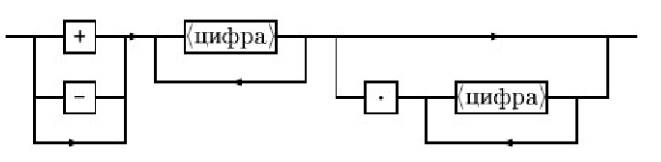
width:400px|Число

Определите ДКА для ввода числа

Определите ДКА, проверяющий что строка из букв a,b,c содержит буквы a и b.
Определите ДКА, проверяющий что строка из букв a,b,c имеет длину 3 и является перестановкой букв a,b,c.

Редактор и исполнитель конечных автоматов