Начало
Учебные материалы
Вычислительные основы
Реальные компьютеры vs. модели вычислений Детерминированный конечный автомат Машина Тьюринга Нормальный алгоритм Маркова Теория рекурсивных функций * Практическое использование
Машина Тьюринга
упростить определение вычислительной модели.
--
Формально машина Тьюринга (МТ) представляет собой кортеж `T=(Sigma, Gamma, Q, q_0, delta, q_{ac cept}, q_{reject})`, где
1. `Sigma` - входной алфавит
2. `Gamma` - ленточный алфавит `Gamma supe Sigma uu {square}`, где `square` – символ, находящийся в пустой ячейке ленты
3. `Q` – конечное множество состояний;
4. `q_0 in Q` – начальное состояние;
5. `delta : Q xx Gamma -> Q xx Gamma xx D` - функция перехода; `delta` вычисляет следующее состояние `(p,b,d) = delta(q, a)`, где `p, q in Q, a,b in Gamma, d in D={larr, rarr}`;
6. `q_{ac cept}, q_{reject} in Q` - допускающее и отвергающее состояние, при достижении этого состояния происходит останов
--
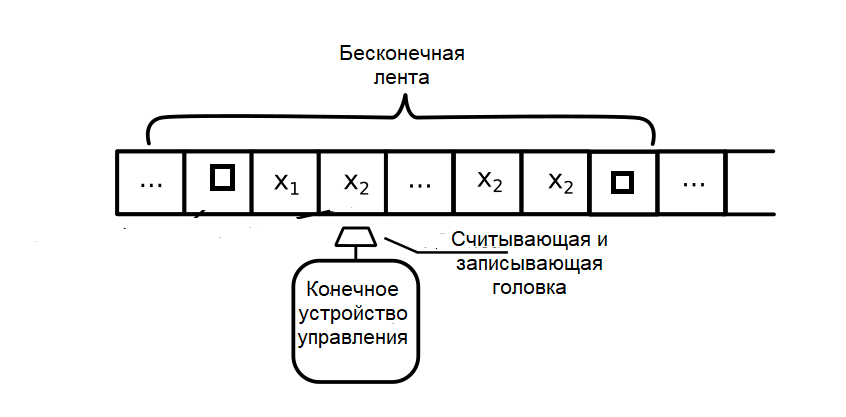
Первоначально входные данные помещаются на ленту, считывающе-записывающая головка ленты расположена на первом символе входных данных,
и состояние равно `q_0`. Все остальные ячейки ленты содержат `square`.
В зависимости от текущего состояния и обозреваемого головкой символа на ленте УУ производит запись нового символа в ячейку,
устанавливает новое состояние и передвигает головку влево или вправо.
Иногда рассматривают `D={larr, rarr, _|_ }`, но при отсутствии движения можно "сжать" переходы, пока не будет выполнено движение головки.
Машина Поста отличается от МТ, то тем что `Sigma=Gamma={0,1}`, что усложняет кодирование входных и выходных данных,
но алгоритмически они эквивалентны.
--
Пример МТ для увеличения двоичного числа на 1: `Sigma={0,1}`, функцию перехода можно описать пятерками `(q, a, p, b, d)` или в форме таблицы:
Символ | `0` | `1`|`square`
--|--|--|--
`q_0` | `(q_0,0,rarr)` | `(q_0,1,rarr)`|`(q_1,square,larr)`
`q_1` | `(q_{ac cept},1, _\|_ )` | `(q_1,0,larr)` |`(q_{ac cept},1, _\|_ )`
`q_0` - движение вправо, пока не дойдем до конца двоичного числа;
`q_1` - заменяем 1 на 0, при обнаружении 0 или `square` пишем 1 и завершаем.
--
Компьютер может имитировать МТ. МТ может имитировать компьютер, причем за время, которое
можно выразить в виде некоторого полинома от числа шагов, совершаемых компьютером.
Также рассматривают недетерминированную МТ (НМТ), но в отличие от НКА пребразование в детерминированную МТ в общем случае невозможно.
Возможно только моделирование, но это приводит к экспоненциальному росту времени выполнения.
У квантовых компьютеров есть сходство с НМТ, но они не могут выполнять моделирование НМТ (и наоборот).
--
Интуитивное понятие алгоритма выражается через формальное определение МТ
*Тезис Тьюринга*
Для любой алгоритмически вычислимой функции существует вычисляющая её значения МТ.
*Универсальная машина Тьюринга* (УМТ) содержит две ленты - одна из которых зарезервирована для программы УУ,
а на другой ленте происходит вычисление.
УУ для УМТ может быть определено с помощью 2 состояний и 3 символов для программы (рекорд 2008 года).
*Теорема о разрешимости* Не существует МТ, которая по программе для УМТ и входным данным могла бы определить завершаемость алгоритма.
---
##### Задания для практики
1. Написать программу для машины Тьюринга, которая переносит первый символ непустого слова из букв a,b,c в его конец.
2. Написать программу для машины Тьюринга, которая уменьшает двоичное число, начинающееся с 1, в 2 раза (убирает последнюю цифру, число из одной цифры заменяет на 0).
3. Написать программу для машины Тьюринга, которая уменьшает двоичное число, начинающееся с 1, на 1.
--
[Машина Тьюринга](viz/turing.html)
