НачалоПодразделы
Другие разделы
| Занятие 1 |
| Занятие 2 |
| Занятие 3 |
| Занятие 4 |
| Занятие 6 |
| Занятие 7 |
| Занятие 8 |
| Занятие 9 |
| Занятие 10 |
| Занятие 11 |
| Занятие 12 |
| Занятие 13 |
| Занятие 14 |
| Занятие 15 |
| Занятие 16 |
| Занятие 17 |
| Занятие 18 |
| Занятие 19 |
| Занятие 20 |
Дата и время
02/05/2024 09:57:07
Занятие 5
Дерево Штерна-Броко
Немного похоже на бинарный поиск работает дерево Штерна-Броко, позволяющее получить множество всех несократимых положительных дробей `m/n`. Начиная с двух дробей 0/1 и 1/0, нужно несколько раз выполнить операцию вставки дробей `(m+m')/(n+n')` между двумя соседними дробями `m/n` и `{m'}/{n'}`.
После первого шага получается последовательность 0/1, 1/1, 1/0, после второго – 0/1, 1/2, 1/1, 2/1, 1/0, после третьего – 0/1, 1/3, 1/2, 2/3, 1/1, 3/2, 2/1, 3/1, 1/0. Верхние уровни дерева выглядят так:
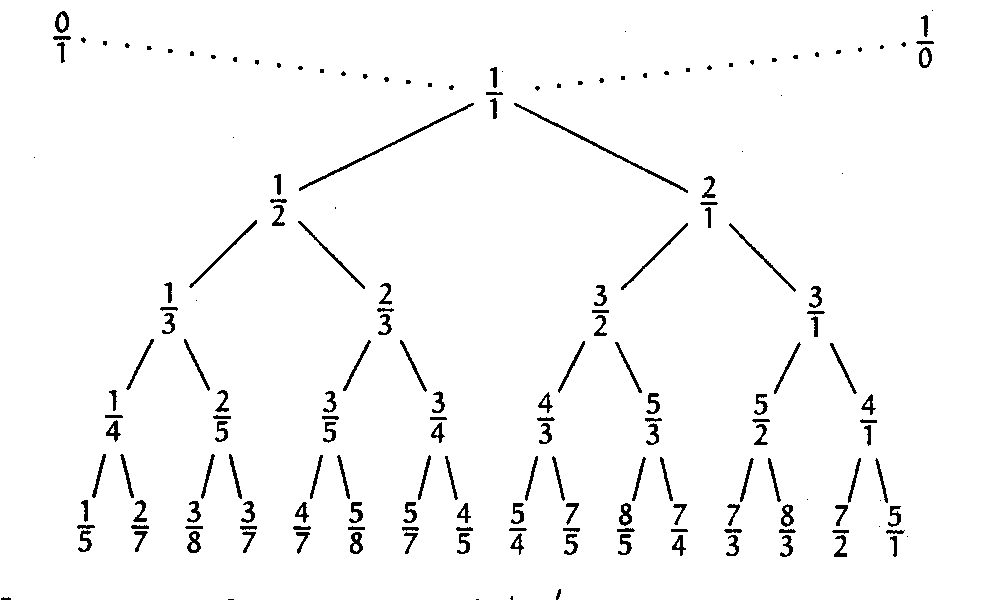
Легко убедиться, что `m/n\ <\ (m+m')/(n+n')\ <\ {m'}/{n'}`. Это значение (медианта) не лежит точно посередине между предшественниками, поэтому для достижения некоторых дробей нужно сделать большее число шагов, чем для других с тем же знаменателем. Если выполнять нахождение медиант только в случае если значение её знаменателя не превосходит `N`, то можно получить последовательность Фарея порядка `N` – множество всех несократимых дробей от 0 до 1, знаменатели которых не превосходят `N`, расположенных в возрастающем порядке.
Дерево Штерна-Броко можно использовать как систему счисления для представления рациональных чисел. Движение вниз по левой ветке будем обозначать L, а по правой – R. Обозначение LRRL соответствует дроби 5/7. Для преобразования дроби `m/n` в эту систему счисления можно использовать следующую программу.
void toSB(int m, int n)
{
while(m!=n)
{ if(m<n)
{ putchar('L');
n-=m;
}
else
{ putchar('R');
m-=n;
}
}
}
Видно, что существует тесная связь между алгоритмом Евклида и представлением Штерна-Броко для рациональных чисел.
Используя аналог алгоритма бинарного поиска можно построить представление Штерна-Броко для иррациональных чисел. Анализируя в какой промежуток попадает число `e`=2.718281828459045, мы получим следующую последовательность медиант 1/1, 2/1, 3/1, 5/2, 8/3, 11/4, 19/7, 30/11, 49/18, 68/25, 87/32, 106/39, 193/71, 299/110, …, которые будут наилучшими рациональными приближениями к числу `e` сверху или снизу. Интересно, что в записи числа `e` в системе Штерна-Броко есть закономерность: `e="RL"^0"RLR"^2"LRL"^4"RLR"^6"LRL"^8"RLR"^10"LRL"^12L…`.
Ускоренная версия:
typedef long long ll;
pair<ll, ll> calc(ll a, ll b = 1000000000000000000LL) {
ll p1 = 0, p2 = 1;
ll q1 = 1, q2 = 0;
while (b != 0) {
ll t = a / b;
p1 += t * p2;
q1 += t * q2;
a -= t * b;
if (q1 > T9) break;
swap(p1, p2);
swap(q1, q2);
swap(a, b);
}
return {p2, q2};
}
