Назад
 Начало Начало |
 Соревнования Соревнования |
| 2008 |
Подразделы
| Разбор задач |
Другие разделы
Дата и время
11/03/2026 20:31:05
 Областная олимпиада школьников по информатике (личное первенство)
Областная олимпиада школьников по информатике (личное первенство)
 5. Горная дорога
5. Горная дорога
 Динамическое программирование и запоминающие функции
Динамическое программирование и запоминающие функцииОлимпиадные задачи на русском языке

| 09/01/2008 | Областная олимпиада школьников по информатике (личное первенство) (5) |
| 10/07/2019 | Лето 2019 - 5 (A) |
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0) 
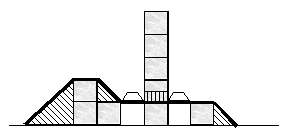
Нужно построить дорогу через горы. В результате предварительных топографических исследований рельеф горной местности был описан как средняя высота на единицу длины. Дорога должна идти либо горизонтально, либо подниматься или спускаться на одну единицу высоты за одну единицы длины. Разные части участка дороги единичной длины могут иметь разный наклон (например, на первой половине участка дорога поднимается вверх на 1/2 единицы высоты, а на второй половине – идет горизонтально).
При строительстве можно строить тоннели через скалы, насыпать грунт, выравнивая рельеф, и строить мосты. Строительство тоннеля обходится в `C_1` за единицу длины. Тоннель может быть только горизонтальным. Стоимость засыпки грунтом ямы высотой в одну единицу и длиной в одну единицу обходится равна `C_2`. Если грунта требуется меньше, например, при создания наклонного участка дороги, то стоимость насыпки грунта прямо пропорционально боковой площади насыпи. Мост может быть только горизонтальным и иметь длину от 1 до 3 единиц длины. Края моста должны упираться в скалы. Стоимость строительства моста равна `C_3` за единицу длины. Дорога должна начинаться и заканчиваться на равнине на высоте 0.
Напишите программу, которая вычислит минимальную стоимость строительства дороги.
В первой строке входного файла содержатся четыре целых числа, разделенных пробелом – длина гор в единицах длины `N` (`1\ ≤\ N\ ≤\ 1000`) и стоимости `C_1`, `C_2`, `C_3` (`1\ ≤\ C_1,\ C_2,\ C_3\ ≤\ 100`). Во второй строке содержатся `N` целых чисел, разделенных пробелами – высоты горных участков в диапазоне от 0 до 1000.
В выходной файл вывести одно число – минимальную стоимость строительства с точностью `10^{-2}`.
Пример ввода (см. рис)
6 7 3 1 2 1 0 5 0 1
Вывод для примера
18.00

