Разбор задач

1. Загадка

Тема: перебор, решето для поиска простых чисел
Сложность: выше среднего

Лобовое решение выглядит так:

var s,t,k,n,i:integer;
begin
  read(s);
  for n:=4 to sqr(s-1) do
  begin
    k:=0;
    t:=0;
    for i:=n div 2 downto 1 do
      if n mod i=0 then
      begin
        inc(k);
        t:=t+i;
        if k=2 then
          break;
      end;
    if (k=2) and (t=s) then
      writeln(n);
  end;
end.

В качестве кандидатов нужно рассматривать числа, не превышающие `(S-1)^2`, так как в худшем случае составное число вида `x^2` будет иметь два наибольших делителя `x` и 1. Время работы этого алгоритма `O(S^4)`. Можно существенно ускорить вычисления, если учесть, что при поиске разложения на простые множители числа `N` можно рассмотреть только числа не превышающие `sqrt(N)`. Наибольшим делителем числа `N` будет `N/a`, где `a` – наименьший простой делитель, а вторым наибольшим делителем будет либо `N/b`, где `b` – второй по величине делитель `N` (также либо простое число, либо `a^2`), либо `a`, если `N` является произведением двух различных простых чисел, либо 1, если `N=a^2`.

var s,t,k,n,i,d:integer;
begin
  read(s);
  for n:=4 to sqr(s-1) do
  begin
    k:=0;
    t:=0;
    d:=1;
    for i:=2 to trunc(sqrt(n)) do
      if n mod i=0 then
      begin
        inc(k);
        t:=t + n div i;
        if i*i<n then d:=i;
        if k=2 then break;
      end;
    if k=1 then
    begin
      t:=t+d;
      inc(k);
    end;
    if (k=2) and (t=s) then
      writeln(n);
  end;
end.

Время работы алгоритма уменьшилось до `O(S^3)`, но остается достаточно большим. Существенно улучшить алгоритм, можно используя самый эффективный способ нахождения простых чисел – решето Эратосфена (вычеркивание из таблицы всех чисел, кратных простым):

const maxn=1000000;
var p:array [2..maxn] of boolean;
  i,j:integer;
begin
  for i:=2 to maxn do
    p[i]:=true;
  for i:=2 to maxn do
    if p[i] then
    begin
      j:=i*i;
      while j<=maxn do
      begin
        p[j]:=false;
        j:=j+i;
      end;
    end;
end.

Для каждого числа нужно найти два наименьших делителя, поэтому массив флагов в алгоритме решета заменяем на два массива целых чисел – наименьший простой делитель и следующий по величине делитель.

const maxn=1000000;
var 
  s,i,i2,j:integer;
  p1,p2:array[2..maxn] of integer;
begin
  read(s);
  for i:=2 to maxn do
  begin
    p1[i]:=1;
    p2[i]:=i;
  end;
  for i:=2 to maxn do
    if p1[i]=1 then { i – простое число }
    begin
      j:=2*i;
      while j<=maxn do
      begin
        if p1[j]=1 then p1[j]:=i
        else if p2[j]>i then p2[j]:=i;
        j:=j+i;
      end;
      { обработка случая, когда вторым делителем
        является квадрат наименьшего делителя }
      if i<=1000 then { чтобы избежать переполнения при умножении }
      begin
        i2:=i*i; 
        j:=i2;
        while j<=maxn do
        begin
          if p2[j]>i2 then p2[j]:=i2;
          j:=j+i2;
        end;
      end;
    end
    else { i – составное число }
      if (i div p1[i])+(i div p2[i])=s then
        writeln(i);
end.

2. Карточки

Тема: поиск максимума, обработка текста
Сложность: низкая

Для каждой буквы считаем, сколько раз она встречается в каждом из слов и находим максимум из этих значений.

var
   n,i,j,m,k:integer;
   w:array [1..100] of string;
   c:char;
begin
  readln(n);
  for i:=1 to n do
    readln(w[i]);
  for c:='A' to 'Z' do
  begin
    m:=0;
    for i:=1 to n do
    begin
      k:=0;
      for j:=1 to length(w[i]) do
        if w[i][j]=c then
          inc(k);
      if k>m then
        m:=k;
    end;
    if m>0 then
      writeln(c,' ',m);
  end;
end.

Нахождение максимума можно совместить с вводом, используя массивы максимумов и количеств для каждой буквы.

var
   n,i,j:integer;
   w:string; 
   c:char;
   k1,ka:array['A'..'Z']of integer;
begin
  readln(n);
  for c:='A' to 'Z' do
    ka[c]:=0;
  for i:=1 to n do
  begin
    readln(w);
    for c:='A' to 'Z' do
      k1[c]:=0;
    for j:=1 to length(w) do
      inc(k1[w[j]]);
    for c:='A' to 'Z' do
      if k1[c]>ka[c] then
        ka[c]:=k1[c];
  end;
  for c:='A' to 'Z' do
  begin
    if ka[c]>0 then
      writeln(c,' ',ka[c]);
  end;
end.

3. ИБП

Тема: моделирование
Сложность: средняя

Если использовать тип shortint (целое от 128 до 127) вместо обычного integer, то можно хранить значения всех измерений (100 x 100000 байт < 32Мб), поступивших от ИБП. Но фактически необходимы только `M` последних значений, которые удобно хранить в кольцевом буфере размера `M`. Также необходимо хранить количество значений меньше и равных `L` в буфере и их сумму. При поступлении очередного измерения от `j`-го ИБП изменяется только сумма и количество для `j`-го ИБП, предыдущее значение удаляется и вычитается из суммы, а новое записывается на его место в кольцевом буфере и прибавляется к сумме. Указатель буфера смещается на следующую позицию.

var N,L,M,K,i,j,p,b:integer;
  q:array[1..100,1..100] of integer;
  ki,li,si:array[1..100] of integer;
begin
  read(N,L,M,K);
  for i:=1 to N do
  begin
    ki[i]:=1;
    li[i]:=0;
    si[i]:=100*M;
    for j:=1 to M do
      q[i,j]:=100;
  end;
  for i:=1 to K do
  begin
    read(j,p);
    si[j]:=si[j]-q[j,ki[j]];
    if q[j,ki[j]]<=L then
      dec(li[j]);
    si[j]:=si[j]+p;
    if p<=L then
      inc(li[j]);
    q[j,ki[j]]:=p;
    inc(ki[j]);
    if ki[j]>M then
      ki[j]:=1;
    b:=0;
    for j:=1 to N do
    begin
      if li[j]=M then
      begin
        if b=0 then
          b:=j
        else if si[j]<si[b] then
          b:=j;
      end;
    end;
    writeln(b);
  end;
end.

4. Ход конем

Тема: поиск в ширину
Сложность: средняя

Для решения можно использовать волновой алгоритм, который заключается в следующем. Начальная позиция помечается значением 0. На `i`-ом шаге нужно найти пометку `i-1` и пометить все непомеченные клетки значением `i`.

var
  n,x,y,x1,y1,i,k,m:integer;
  u:array[1..100,1..100] of integer;
procedure xod(x2,y2:integer);
begin
  if (x2<1) or (x2>n) or (y2<1) or (y2>n) then
    exit;
  if u[x2,y2]>=0 then exit;
  u[x2,y2]:=i;
  inc(m);
end;
begin
  read(n,x,y,k);
  m:=1;
  for x1:=1 to n do
    for y1:=1 to n do
      u[x1,y1]:=-1;
  u[x,y]:=0;
  for i:=1 to k do
    for x:=1 to n do 
      for y:=1 to n do
        if u[x,y]=i-1 then
        begin
          xod(x+1,y+2);
          xod(x-1,y+2);
          xod(x+1,y-2);
          xod(x-1,y-2);
          xod(x+2,y+1);
          xod(x-2,y+1);
          xod(x+2,y-1);
          xod(x-2,y-1);
        end;
  writeln(m);
end.

Время работы этого алгоритма равно `O(N^2*K)`, что вполне укладывается в 1 секунду. Время можно уменьшить до `O(N^2)`, если использовать поиск в ширину, и новые отмеченные клетки заносить в очередь

var
  n,x,y,x1,y1,k1,k,q1,q2,m:integer;
  q:array[1..10000] of record x,y:integer; end;
  u:array[1..100,1..100] of integer;
procedure xod(x2,y2:integer);
begin
  if (x2<1) or (x2>n) or (y2<1) or (y2>n) then
    exit;
  if u[x2,y2]>=0 then exit;
  u[x2,y2]:=k1;
  inc(m);
  q[q2].x:=x2;
  q[q2].y:=y2;
  inc(q2);
end;
begin
  read(n,x,y,k);
  q[1].x:=x;
  q[1].y:=y;
  q1:=1;
  q2:=2;
  m:=1;
  for x1:=1 to n do
    for y1:=1 to n do
    u[x1,y1]:=-1;
  u[x,y]:=0;
  while q1<q2 do
  begin
    x:=q[q1].x;
    y:=q[q1].y;
    inc(q1);
    if u[x,y]<k then
    begin
      k1:=u[x,y]+1;
      xod(x+1,y+2);
      xod(x-1,y+2);
      xod(x+1,y-2);
      xod(x-1,y-2);
      xod(x+2,y+1);
      xod(x-2,y+1);
      xod(x+2,y-1);
      xod(x-2,y-1);
    end;
  end;
  writeln(m);
end.

5. Горная дорога

Тема: динамическое программирование
Сложность: высокая

Вычисление производится методом динамического программирования. Элемент матрицы `T[i,j]` содержит минимальную стоимость для проведения дороги в позицию после `i`-го участка горного рельефа на высоту `j`. `T[0,j]` вычисляется как `j^2*C_2/2`, так как попасть на высоту `j` можно только построив насыпь.

При вычислении `T[i,j]` возможны три случая.

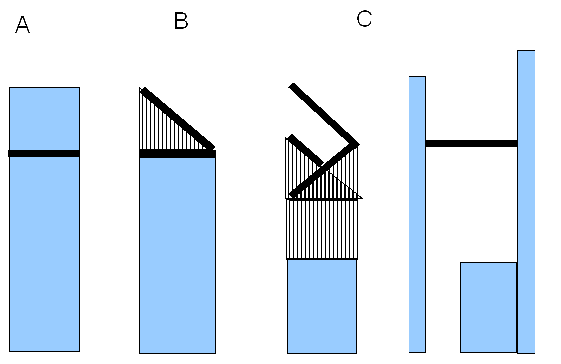
A. Если высота `i`-го участка рельефа выше `j`, то попасть в эту точку можно только с помощью прокладки туннеля: `T[i,j]=T[i-1,j]+C_1`.

B. Если высота `i`-го участка рельефа равна `j`, то попасть в эту точку можно либо проведя дорогу по поверхности горы, либо построив наклонную насыпь с большей высоты: `T[i,j]=min(T[i-1,j],T[i-1,j+1]+C_2/2)`.

C. Если высота `i`-го участка рельефа меньше `j`, то попасть в эту точку можно либо построив наклонную насыпь с большей или меньшей высоты, либо построив v-образную дорогу (насыпать дорогу горизонтально нет смысла), либо построить мост, если возможно (далее на высоте j должна быть скала для правой опоры моста, и не более чем в 3 единицах должна быть скала для левой опоры моста). `T[i,j]=min(\ min(T[i-1,j]-C_2/4,T[i-1,j+1]+C_2/2,T[i-1,j-1]-C_2/2)\ +\ (j-h[i])*C_2,\ "вариант"\ с\ "мостом")`.

После заполнения матрицы нужно найти минимум среди значений `T[n,j]+\ j^2*C_2/2`.

var N,i,j,k,c1,c2,c3:integer;
  h:array[1..1000] of integer;
  t:array[0..1000,0..1000] of extended;
  r:extended;
procedure setmin(v:extended);
begin
  if v<t[i,j] then t[i,j]:=v;
end;
begin
  read(n,c1,c2,c3);
  for i:=1 to n do
    read(h[i]);
  for j:=0 to 1000 do
    t[0,j]:=j*j/2*c2;
  for i:=1 to n do
    for j:=0 to 1000 do
    begin
      if h[i]>j then
        t[i,j]:=t[i-1,j]+c1
      else if h[i]=j then
      begin
        t[i,j]:=t[i-1,j];
        if j<1000 then setmin(t[i-1,j+1]+c2/2);
      end
      else
      begin
        t[i,j]:=t[i-1,j]+(j-h[i])*c2-c2/4;
        if j<1000 then setmin(t[i-1,j+1]+(j-h[i])*c2+c2/2);
        setmin(t[i-1,j-1]+(j-h[i])*c2-c2/2);
        if (i<n) and (h[i+1]>=j) then
        begin
          for k:=1 to 3 do
            if (i>k) and (h[i-k]>=j) then
            begin
              setmin(t[i-k,j]+k*c3);
              break;
            end;
        end;
      end;
    end;
  r:=t[n,0];
  for j:=1 to 1000 do
    if r>t[n,j]+j*j/2*c2 then
      r:=t[n,j]+j*j/2*c2;
  writeln(r:1:2);
end.