Подразделы

Другие разделы

Дата и время

01/04/2025 04:52:12

Авторизация

Зарегистрироваться
Восстановить пароль

Вычислительная геометрия

Представление геометрических объектов Алгоритмы

Алгоритмы

Площадь многоугольника

Площадь многоугольника через векторное произведение может вычислена следующим образом:

double Square(vector<Point>& a){
  double s=0;
  for(int i=2; i<a.size(); ++i)
    s+=(a[i-1]-a[0])^(a[i]-a[0]);
  return fabs(s/2);
}

Пересечение отрезков

int sign(double a){ return a==0?0:(a<0?-1:1); }

bool isCrossed(Point p1, Point p2, Point p3, Point p4) {
  return (max(min(p1.x,p2.x),min(p3.x,p4.x)) <= min(max(p1.x,p2.x),max(p3.x,p4.x)) &&
        max(min(p1.y,p2.y),min(p3.y,p4.y)) <= min(max(p1.y,p2.y),max(p3.y,p4.y)) &&
        sign((p3-p1)^(p2-p1))*sign((p4-p1)^(p2-p1))<=0 &&
        sign((p1-p3)^(p4-p3))*sign((p2-p3)^(p4-p3))<=0);
}

Точка пересечения отрезков

Вариант 1

Реализация

Проверить, что отрезки пересекаются.
Преобразовать отрезки в коэффициенты прямой $Ax+By+C=0$

A = s.first.y - s.second.y;
B = s.second.x - s.first.x;
C = -A*s.first.x - B*s.first.y;

Найти точку пересечения прямых

Вариант 2 (более простой)

Представить отрезок в форме

${ (x=x_1+alpha*(x_2-x_1)), (y=y_1+alpha*(y_2-y_1)) :}$ , где $alpha in [0;1]$

Тогда нужно решить систему уравнений

${ (x_1+alpha_1*(x_2-x_1)=x_3+alpha_2*(x_4-x_3)), (y_1+alpha_1*(y_2-y_1)=y_3+alpha_2*(y_4-y_3)) :}$

и проверить, что $alpha_1 in [0;1] ^^ alpha_2 in [0;1]$

Можно использовать для нахождения точки пересечения прямых, прямой и отрезка, лучей и т.д.

${ (alpha_1*(x_2-x_1)-alpha_2*(x_4-x_3)=x_3-x_1), (alpha_1*(y_2-y_1)-alpha_2*(y_4-y_3)=y_3-y_1) :}$

$[[(x_2-x_1),-(x_4-x_3)],[(y_2-y_1),-(y_4-y_3)]]$

const double EPS=1e-9;
double alpha(Point a, Point b) {
  if(fabs(a.x)<=fabs(a.y)) return b.y/a.y;
  return b.x/a.x;
}
double minalpha(Point a, Point b, Point c) {
  double a1=alpha(a,b),a2=alpha(a,c);
  if(a1>a2) swap(a1,a2);
  if(a1<=0) return min(a2,0.0);
  return a1;
}
optional<pair<double,double>> crossAt(Point p1, Point p2, Point p3, Point p4) {
  Point a=p2-p1,b=p3-p4,c=p3-p1;
  double d=a^b; // определитель
  if(fabs(d)<=EPS) {
    if(fabs(c^a)>EPS) return {};
    return {{minalpha(a,c,p4-p1),minalpha(b,p3-p2,c)}};
  }
  return {{(c^b)/d,(a^c)/d}};
}
int main()
{
 auto r=crossAt(p1,p2,p3,p4);
 if(r) {
   Point p=(p2-p1)*r->first+p1;
   print("Yes\n{} {}\n",p.x,p.y);
 }
 else
   print("No\n");
}

Точки пересечения для $N$ отрезков.

width:150px;float:right|Задача

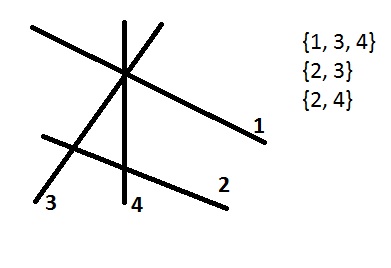
Методом грубой силы $O(N^2)$ , а с помощью сканирующей прямой $O((N+K) log N)$ , где $K$ – количество точек пересечения (в худшем случае $N^2/2$ ).

Алгоритм Бентли-Оттмана находит номера отрезков, которые пересекаются.

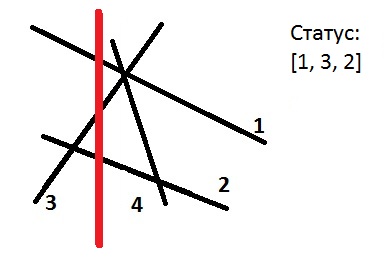width:150px;float:right|Статус При использовании сканирующей прямой сначала нужно упорядочить концы отрезков по координате $x$ . Далее при движении слева-направо нужно отслеживать 3 типа события:

начался новый отрезок
два отрезка пересеклись
отрезок закончился

Номера отрезков, пересекающих сканирующую прямую, должны быть упорядочены по возрастанию координаты $y$ их пересечения с прямой: $O(N log N)$ . В процессе работы отрезки могут добавляться в произвольные места этого упорядоченного множества, удаляться из произвольных места или меняться местами друг с другом.

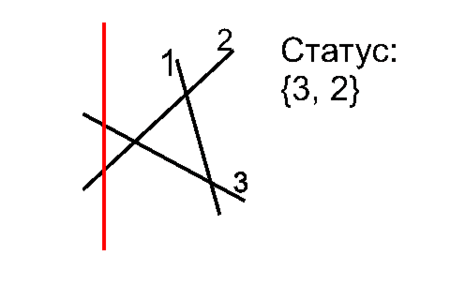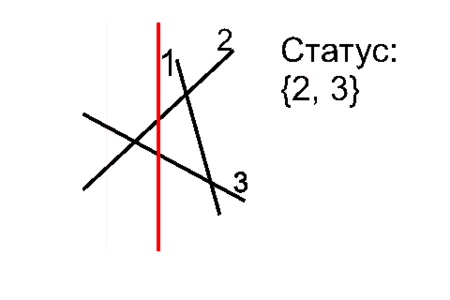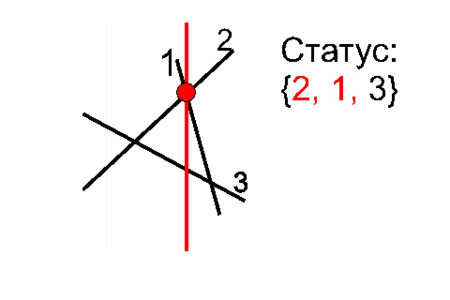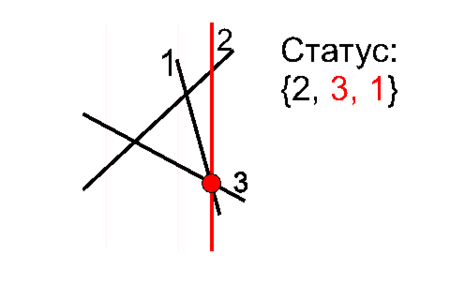width:150px;float:right|Статус Пересекаться могут соседние отрезки. Поэтому при добавлении нового отрезка нужно добавить в события координаты $x$ пересечения с отрезком выше и ниже, если такие есть: $O(log N)$ .

При удалении отрезка соседними становятся отрезки выше и ниже, нужно проверить и добавить координату $x$ пересечения, если такое есть: $O(log N)$ .

При обработке события пересечения нужно поменять местами отрезки и проверить на появление новых точек пересечения с новыми соседями: $O(log N)$ .

В алгоритме нужно учесть вертикальные отрезки, пересечение нескольких отрезков в одной точке, наложение отрезков (можно заменить 1 отрезком).

Назад