 Линейные АТД
Линейные АТД
 Массив и Строка
Массив и Строка
Различают массивы переменного и фиксированного размера. Базовые операции для массива:
Операция|Эффективность|Вызов
--|--|--
конструктор `n` элементов |`O(n)`| ``std::vector<int> s(10);``\
``std::array<int,10> s;``
количество элементов | `O(1)` | ``auto len=s.size();`` или ``ssize(s);``
`i`-й элемент | `O(1)` | ``auto x=s[i]; s[i]=x;``\
или ``s.at(i)`` с проверкой
получение итератора на первый элемент (конец массива) | `O(1)` | ``auto f=s.begin(), e=s.end();``
Итератор массива можно перемещать на произвольное количество элементов за `O(1)` с помощью операций ``+=`` и ``-=``.
``vector`` поддерживает интерфейсы АТД Список и АТД Массив.
Так как ``array`` имеет фиксированный размер, то он не поддерживает операции вставки, удаления и создания пустого списка (только длину и получение итератора для последовательного доступа). Недостаток: нельзя определить обычную функцию (не шаблон), которой можно передавать аргумент ``array`` разных размеров.
После вставки или удалении элементов итераторы для ``vector`` становятся недействительными.
Варианты реализации массива:
* массив фиксированного размера языка C;
* массив фиксированного размера ``array``;
* массив переменного размера ``vector`` реализуется как структура с полями текущий размер, выделенный размер, указатель на массив выделенного размера;
* если требуется быстрые операции вставки и удаления, то через нелинейную структуру данных
В классе ``vector`` в случае нехватки выделенного размера для добавления элемента происходит выделение памяти для массива в 2 раза большего размера. Это позволяет обеспечить амортизированную оценку `O(1)` для операции добавления в конец массива.
Пример нелинейной структуры данных для массива (корневая декомпозиция):
Последовательность из `N` элементов делится на кусочки по `|~ sqrt(N) ~|` элементов. В массиве-каталоге размером `|~ sqrt(N) ~|` записывается количество элементов `C_j` в каждом куске и указатель на каждый кусок. Так как в кусок могут добавляться новые значения, для куска можно выделить память для `2*|~ sqrt(N) ~|` элементов.
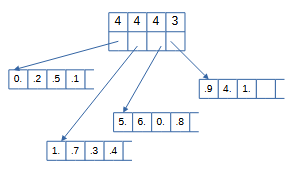
Для получения `i`-го элемента сначала за `O(sqrt(N))` действий находим по массиву-каталогу номер куска `k` и за `O(1)` берем элемент с номером `(i-sum_{j=0}^k C_j)` из куска `k`. При добавлении и удалении изменяем соответствующий кусок последовательности за `O(sqrt(N))`. На рисунке показано изменение структуры данных после изменения 11-го элемента на -2, удаления 13-го и добавления 2 после 5-го и 0.6 после 9-го. `M` операций может быть выполнено за `O(M*sqrt(N))`.
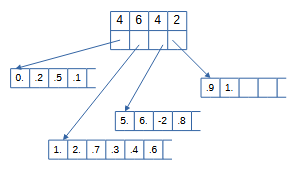
Через каждые `O(sqrt(N))` операций добавления и удаления необходимо обновлять структуру, чтобы размеры кусков снова стали `|~ sqrt(N) ~|`. Это может быть выполнено за `O(N)`. Если выполняется `M` операций, то потребуется `M//sqrt(N)` обновлений, суммарно `O(N*M//sqrt(N))=O(M*sqrt(N))`. В сумме `O(M*sqrt(N))` на выполнение операций и `O(M*sqrt(N))` на обновления дают эффективность `O(M*sqrt(N))`.
При размере последовательности `10^6` элементов операции вставки и удаления будут выполняться в 1000 раз быстрее по сравнению с ``vector``, но операции доступа к элементам выполняются в 1000 раз медленнее.
Но если количество операций добавления и удаления составляет хотя 1% от количества операций доступа к элементам, то выгодно использовать именно такую структуру.
В следующем разделе будут рассмотрены структуры данных с эффективностью `O(log N)` для всех операций.
АТД Строка является массивом переменного размера из символов.
Базовые операции для строк:
Операция|Эффективность|Вызов
--|--|--
конструктор (пустая строка)|`O(1)`|``string s;``
конструктор (`n` символов)|`O(n)`|``string s(n,'A');``
длина строки|`O(1)`|``size_t len=s.length();``
`i`-й символ | `O(1)` | ``auto x=s[i]; s[i]=x;``\
или ``s.at(i)`` с проверкой
сцепление строк|`O(n)`|``s=s1+s2;``
подстрока|`O(n)`|``s=s1.substr(pos,n);``
замена символов|`O(n)`|``s.replace(pos,n,s1);``
удаление символов|`O(n)`|``s.erase(pos,n);``
вставка символов|`O(n)`|``s.insert(pos,s1); s.insert(pos,k,'A');``
Кроме этого, ``string`` обеспечивает интерфейс АТД Список.
В классе ``string`` STL используется приём [Small String Optimization](https://habr.com/ru/companies/oleg-bunin/articles/352280/). Строка длиной до 15 символов хранится в массиве фиксированного размера внутри объекта, и только при превышении этого ограничения выделяется динамическая память. Это позволяет существенно ускорить вычисления, так как коротких строк в программе обычно на порядок больше, чем длинных.
[Структура данных *строп*](https://ru.wikipedia.org/wiki/%D0%A1%D1%82%D1%80%D0%BE%D0%BF_(%D1%81%D1%82%D1%80%D1%83%D0%BA%D1%82%D1%83%D1%80%D0%B0_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85)) (rope) позволяет ускорить операции сцепления и выделения подстроки для очень длинных строк до `O(log k)`, где `k` -- количество кусков в строке. Обычно используется для неизменяемых строк.

 Начало
Начало Учебные материалы
Учебные материалы