 Методы грубой силы
Методы грубой силы
Идея методов грубой силы Последовательный поиск Исчерпывающий перебор Сортировки методом грубой силы
 Исчерпывающий перебор
Исчерпывающий перебор
который можно описать как комбинаторный объект (перестановка, сочетание, размещение или подмножество).
Многие подобные задачи являются задачами оптимизации: в них требуется найти элемент, который максимизирует
или минимизирует некоторые интересующие нас характеристики, как, например,
длина пути или назначенная стоимость.
--
*Исчерпывающий перебор* представляет собой подход к
таким задачам с позиции грубой силы. Он предполагает генерацию всех
возможных комбинаторных объектов из области определения задачи, выбор тех из них, которые
удовлетворяют ограничениям, накладываемым условием задачи, и последующий
поиск нужного объекта (например, оптимизирующего значение целевой
функции задачи). Заметим, что, хотя идея исчерпывающего перебора весьма проста, ее
реализация обычно требует алгоритма для генерации определенных
комбинаторных объектов.
--
##### Поиск пары ближайших точек
Задача поиска пары ближайших точек заключается в том, чтобы во множестве
из `n` точек найти две, расположенные друг к другу ближе других. Для
простоты мы будем рассматривать только двумерный случай, хотя задача может быть
поставлена и для большего числа измерений. Точки задаются стандартным
способом с помощью декартовых координат `(x, y)`, а расстояние между двумя точками
`P_i =(x_i,y_i)` и `P_j=(x_j,y_j)` представляет собой евклидово расстояние
`d(P_i,P_j) = sqrt{(x_i -x_j)^2+(y_i-y_j)^2}`
Подход с применением грубой силы для решения этой задачи приводит нас
к следующему очевидному алгоритму: вычислить расстояния между каждой парой
точек и найти пару с наименьшим расстоянием. Естественно, мы хотим избежать
повторного вычисления расстояния между одними и теми же точками, поэтому
рассматриваем только пары точек, для которых `i < j`.
--
Алгоритм ClosestPoints (`P`)
// Входные данные: список `P[0...n-1]`, где `P_i=(x_i,y_i), n>=2`
// Выходные данные: индексы `(a,b)` пары ближайших точек
`d_{min} larr +oo`
**for** `i in [0...n-2]` **do**
`quad` **for** `j in [i+1...n-1]` **do**
`quad quad d larr sqrt{(x_i -x_j)^2+(y_i-y_j)^2}`
`quad quad ` **if** `d < d_{min}`
`quad quad quad quad d_{min} larr d; a larr i; b larr j`
**return** `(a,b)`
--
Основной операцией алгоритма является вычисление расстояния между двумя
точками. Квадратный корень может быть вычислен только приближенно, кроме того, эта операция
выполняется в 10-20 раз медленнее операций умножения и сложения.
Но вычисления квадратного корня в алгоритме вполне можно избежать! После замены
`d larr sqrt{(x_i -x_j)^2+(y_i-y_j)^2}` на
`d larr (x_i -x_j)^2+(y_i-y_j)^2` основной операцией алгоритма станет возведение чисел в квадрат (умножение).
Общее количество таких операций можно вычислить следующим образом:
`C(n)=sum_{i=0}^{n-2} sum_{j=i+1}^{n-1} 2 = n^2- n in Theta(n^2)`
--
##### Задача коммивояжера
Найти кратчайший путь по заданным `n` городам, чтобы каждый
город посещался только один раз и конечным пунктом оказался город, с которого
начиналось путешествие.
Проблему удобно смоделировать при помощи взвешенного графа, вершины которого представляют города, а веса ребер определяют
расстояния.
После этого задача может быть сформулирована как задача
поиска кратчайшего *гамильтонового цикла* неориентированного
графа (цикл, который проходит по всем вершинам
графа ровно по одному разу).
--
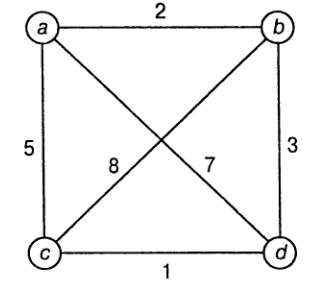
Без потери общности можно предположить, что все циклы начинаются и заканчиваются в одной конкретной вершине Значит,
можно получить все возможные маршруты, генерируя все перестановки `n-1` промежуточных городов, вычисляя длину соответствующих
путей и находя кратчайший из них. Также существуют пары обходов,
которые отличаются друг от друга только направлением.
Путь|Длина
--|--
`a->b->c->d->a` | 2+8+1+7=18
`a->b->d->c->a` | **2+3+1+5=11**
`a->c->b->d->a` | 5+8+3+7=23
`a->c->d->b->a` | **5+1+3+2=11**
`a->d->b->c->a` | 7+3+8+2=23
`a->d->c->b->a` | 7+1+8+2=18
Количество возможных перестановок равно `(n-1)!//2`, что делает исчерпывающий
перебор неприемлемым для больших значений `n`.
--
##### Задача о рюкзаке
Дано `n` предметов весом `w_1,..., w_n` и стоимостью `v_1,..., v_n`, а также рюкзак, выдерживающий вес `W`. Требуется
найти подмножество предметов, которое можно разместить в рюкзаке, и которое имеет при этом максимальную стоимость.
Исчерпывающий перебор в этой задаче приводит к рассмотрению всех
подмножеств данного множества из `n` предметов, вычислению общего веса каждого
из них для того, чтобы выяснить, допустим ли такой набор предметов (т.е. не
превосходит ли его общий вес `W`), и выбору из допустимых
подмножества с максимальной стоимостью.
--
Номер|Вес|Стоимость
-|-|-
1|7|42
2|3|12
3|4|40
4|5|25
В рюкзак можно поместить не более `W=10`.
Подмножество|Общий вес|Общая стоимость
--|--|--
`O/`|0|0
1|7|42
2|3|12
3|4|40
4|5|25
{1,2}|10|64
{1,3}|11|`>W`
{1,4}|12|`>W`
{2,3}|7|52
{2,4}|8|37
{3,4}|9| **65**
{1,2,3}|14|`>W`
{1,2,4}|15|`>W`
{1,3,4}|16|`>W`
{2,3,4}|12|`>W`
{1,2,3,4}|19|`>W`
--
Поскольку общее
количество подмножеств `n`-элементного множества равно `2^n`, исчерпывающий
перебор приводит к алгоритму со временем работы `Omega(2^n)`, вне зависимости от того,
насколько эффективным методом генерируются рассматриваемые подмножества.
Эти две задачи представляют собой наиболее известные примеры так называемых *NP-сложных задач*.
Ни для одной из NP-сложных задач не известен алгоритм, решающий их за
полиномиальное время.
--
#### Задача о назначениях
Имеется `n` работников, которые должны выполнить `n` заданий, по
одному заданию каждый (т.е. каждому работнику назначается только одно задание,
и каждое задание назначается лишь одному человеку).
Стоимость выполнения `i`-м работником `j`-го задания известна и равна `C_{ij}`.
Задача заключается в следующем: надо распределить задания между работниками
таким образом, чтобы они были выполнены с наименьшей общей стоимостью.
В терминах матрицы стоимости `C` в задаче требуется
выбрать по одному элементу из каждой строки матрицы так, чтобы выбранные
элементы находились в разных столбцах, а их общая сумма имела наименьшее
возможное значение.
--
Нельзя выбирать наименьшие элементы в каждой строке, поскольку они могут оказаться в одном и том же столбце.
В действительности, наименьшие элементы матрицы могут вообще не входить в оптимальное
решение. Так что исчерпывающий перебор для решения данной задачи может
оказаться неизбежен.
Допустимое решение задачи о назначениях можно описать в виде кортежа из `n`
значений `(a_1, ..., a_n)`, в котором `i`-й компонент указывает номер задания,
назначенного `i`-му работнику.
--
Имеется однозначное соответствие между допустимыми назначениями и
перестановками первых `n` натуральных чисел. Следовательно, исчерпывающий перебор для
задачи о назначениях может потребовать генерации всех перестановок
натуральных чисел `1,2,...,n`, вычисления общей стоимости каждого назначения путем
суммирования соответствующих элементов матрицы стоимости и окончательного
выбора назначения с минимальной стоимостью, Что приводит к алгоритму `Omega(n!)`.
К счастью, для данной задачи имеется *венгерский алгоритм* с оценкой эффективности `O(N^3)`.
---
##### Задания для практики
1. Задача поиска пары ближайших точек заключается в том, чтобы во множестве из `n` точек найти две, расположенные друг к другу ближе других. Можно разработать более быстрый алгоритм, основанный на методе грубой силы, с помощью которого выполнялся бы поиск пары ближайших точек для `n` точек `x_1,... ,x_n` на действительной оси координат?
2. Предложите алгоритм для поиска самых удаленных точек. Как его можно улучшить?
3. Предложите алгоритм для поиска, какую минимальную площадь поверхности может иметь параллелепипед, сложенный из `N` кубиков единичного размера.
4. Даны `n` натуральных чисел, которые надо разбить на два непересекающихся подмножества с одинаковой суммой их элементов (понятно, что задача не всегда имеет решение). Разработайте алгоритм решения данной задачи на основе исчерпывающего перебора. Постарайтесь минимизировать количество подмножеств, которые должен сгенерировать алгоритм.

 Начало
Начало Учебные материалы
Учебные материалы