 Математические основы анализа алгоритмов
Математические основы анализа алгоритмов
Асимптотические обозначения Основные классы эффективности Индукция и инвариант Нижние границы эффективности Тривиальная нижняя граница Информационно-теоретическая нижняя граница
 Асимптотические обозначения
Асимптотические обозначения
можно использовать порядок роста количества базовых операций алгоритма.
Через `t(n)` мы обозначим время выполнения алгоритма. Оно выражается в виде числа
основных операций алгоритма, обозначаемых через `C(n)`. Под `g(n)` мы будем
понимать некоторую простую функцию, с которой будет проводиться сравнение
количества операций.
--
##### Нестрогое введение
Обозначение `O(g(n))` — это множество всех функций,
порядок роста которых при достаточно больших `n` не превышает (т.е. меньше или
равен) некоторую константу, умноженную на значение функции `g(n)`.
Например:
`n in O(n^2)`, `100n+5 in O(n^2)` , `n(n-1)//2 in О(n^2)`.
С другой стороны,
`n^3 !in O(n^2)`, `0.0001 n^3 !in O(n^2)`, `n^4 + n + 1 !in O(n^2)`.
--
Второе обозначение, `Omega(g(n))`, —
это множество всех функций, порядок роста
которых при достаточно больших `n` не меньше (т.е. больше или равен) некоторой
константы, умноженной на значение функции `g(n)`. Например:
`n^3 in Omega(n^2)`, `n(n-1)//2 in Omega(n^2)` , но `100n+5 !in Omega(n^2)`.
Обозначение `Theta(g(n))` —
это множество всех функций, порядок роста
которых при достаточно больших `n` равен некоторой константе, умноженной на
значение функции `g(n)`. Таким образом, любая квадратичная функция
`a n^2 + bn + c` при `a > 0` принадлежит множеству в `Theta(n^2)`.
Кроме того, среди бесконечного количества других функций множеству `Theta(n^2)` принадлежат также
функции `n^2 + sin n` и `n^2 + log n`.
--
````div
```div
##### `O`-обозначение
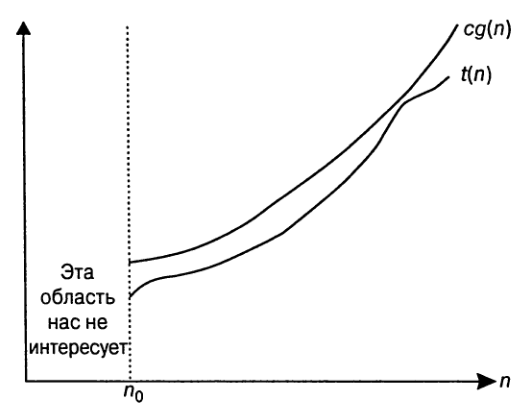
*Определение*. Говорят, что функция `t(n)` принадлежит множеству `O(g(n))`,
если для всех больших значений `n` функция `t(n)` ограничена сверху некоторой константой, умноженной на значение функции
`g(п)`, т.е. если существует положительная константа `c` и неотрицательное целое
число `n_0` такое, что `t(n) <= c*g(n)` для всех `п>=n_0`.
Докажем, что `100n+5 in O(n^2)`
`100n + 5 <= 100n + 5n = 105n <= 105n^2` для всех `n>=1`.
В данном случае `c = 105`, а `n_0 = 1`.
```
````
--
````div
```div
##### `Omega`-обозначение
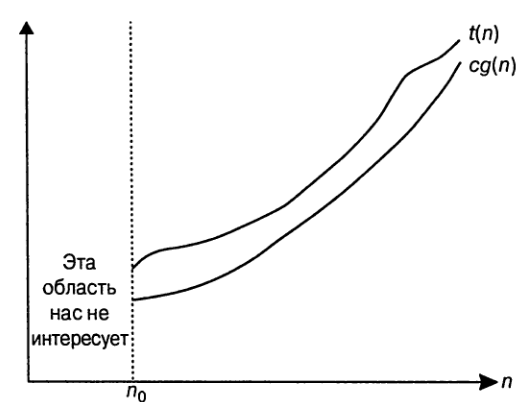
*Определение*. Говорят, что функция `t(n)` принадлежит множеству `Omega(g(n))`,
если для всех больших значений `n` функция
`t(n)` ограничена снизу некоторой константой, умноженной на значение функции
`g(n)`, т.е. если существует положительная константа `c` и неотрицательное целое
число `n_0`, такое, что `t(n) >= c*g(n)` для всех `n>=n_0`.
`n^3 in Omega(n^2)` так как для всех `n>=0` выполняется неравенство `n^3 >= n^2`. Таким образом,
для данного случая можно положить `c = 1` и `n_0 =0`.
```
````
--
````clear:both|div
```div
##### `Theta`-обозначение
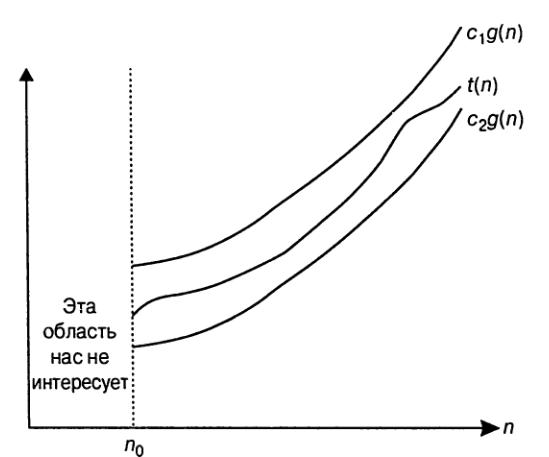
*Определение*. Говорят, что функция `t(n)` принадлежит множеству `Theta(g(n))`,
если для всех больших значений `n`
функция `t(n)` ограничена снизу и сверху некоторыми константами, умноженными на
значения функции `g(n)`, т.е. если существуют положительные константы `c_1` и `c_2`,
а также неотрицательное целое число `n_0` такое, что `c_2 g(n) <= t(n) <= c_1 g(n)` для
всех `n >= n_0`.
```
````
--
Докажем, что `n(n-1)//2 in Theta(n^2)`.
Сначала докажем правую часть неравенства (т.е. определим
верхнюю границу). Для всех `n>= 0` справедливо следующее:
`1/2 n*(n-1)=1/2 n^2- 1/2 n <= 1/2 n^2`
Затем докажем левую часть неравенства (т.е. определим нижнюю границу).
Для всех `n >= 2` справедливо следующее:
`1/2 n*(n-1)=1/2 n^2- 1/2 n >= 1/2 n^2- 1/2 n 1/2 n = 1/4 n^2`
Таким образом, для данного случая можно положить `c_1=1//2`,`c_2 = 1//4`,
`n_0 = 2`.
--
*Теорема*. Если `t_1(n) in O(g_1(n))` и `t_2(n) in O(g_2(n))` то
`t_1(n) + t_2(n) in O(max(g_1(n),g_2(n)))`.
При анализе эффективности
алгоритмов, состоящих из двух исполняемых частей, общая
эффективность алгоритма зависит от той части, которая имеет наибольший
порядок роста, т.е. от наименее эффективной его части:
Аналогичные теоремы справедливы также для множеств `Omega` и `Theta`.
--
Например, проверить, содержит ли массив повторяющиеся элементы, можно
сначала отсортировать массив, затем нужно пройтись по всем элементам
отсортированного массива и проверить,
не дублируют ли соседние элементы друг друга.
Если в алгоритме сортировки, используемом на первом этапе,
выполняется не более чем `n(n - 1)//2` операций сравнения
(т.е. он принадлежит множеству `O(n^2)`), а в
алгоритме, используемом на втором этапе, выполняется не более чем `(n - 1)` операций
сравнения (т.е. он принадлежит множеству `О(n)`), суммарная эффективность
общего алгоритма будет принадлежать множеству `O(max(n, n^2)) = O(n^2)`.
--
При сравнении порядков роста двух конкретных функций
можно обойтись без строгих определений множеств `O`, `Omega`, `Theta`.
Дело в том, что существует более удобный метод выполнения этой оценки, основанный на вычислении
предела отношения двух рассматриваемых функций. Может существовать три
основных случая:
`lim_{n->oo} (t(n))/(g(n))`|Значение|Множества
--|--|--
0 | `t(n)` имеет меньший порядок роста, чем `g(n)`|`t(n) in O(g(n))`
`c` | `t(n)` имеет тот же порядок роста, что и `g(n)` | `t(n) in O(g(n))`, `t(n) in Theta(g(n))`, `t(n) in Omega(g(n))`
`oo` | `t(n)` имеет больший порядок роста, чем `g(n)`|`t(n) in Omega(g(n))`
--
При нахождении предела можно воспользоваться правилом Лопиталя:
`lim_{n->oo} (t(n))/(g(n))=lim_{n->oo} (t'(n))/(g'(n))`
и формулой Стирлинга:
`n! ~~ sqrt(2 pi n)(n/e)^n`
--
Сравните порядки роста функций `n(n - 1)//2` и `n^2`.
`lim_{n->oo} (n(n - 1)//2)/(n^2)=1/2 lim_{n->oo} (n^2 - n)/(n^2)=lim_{n->oo} (1-1/n)=1/2`
Сравните порядки роста функций `log_2 n` и `sqrt(n)`
`lim_{n->oo} (log_2 n)/(sqrt(n))=lim_{n->oo} ((log_2 n)')/((sqrt(n))')=`
`=lim_{n->oo} ((log_2 e) 1/n)/(1/(2 sqrt(n)))=2 log_2 e lim_{n->oo} sqrt(n)/n=2 log_2 e lim_{n->oo} 1/sqrt(n)=0`
--
Сравните порядки роста функций `n!` и `2^n`.
`lim_{n->oo} (n!)/(2^n) = lim_{n->oo} (sqrt(2 pi n)(n/e)^n)/(2^n)=lim_{n->oo} sqrt(2 pi n) (n/(2e))^n=oo`
---
##### Задания для практики
1. Определите истинны или ложны перечисленные ниже утверждения:\
а) `{n(n+1)}/2 in O(n^3)`\
б) `{n(n+1)}/2 in O(n^2)`\
в) `{n(n+1)}/2 in Theta(n^3)`\
г) `{n(n+1)}/2 in Omega(n)`\
2. Для каждой из приведенных ниже функций укажите класс `Theta(g(n))`, к которому относится функция (используйте максимально простую функцию `g(n)`).\
а) `(n^2+1)^10`\
б) `sqrt{10n^2+7n+3}`\
в) `2n "lg"(n+2)^2+(n+2)^2 "lg"(n//2)`\
г) `2^{n+1}+3^{n-1}`\
д) `|__ log_2 n __|`

 Начало
Начало Учебные материалы
Учебные материалы