Математические основы анализа алгоритмов

Информационно-теоретический подход пытается установить нижнюю границу алгоритма на основе количества информации, которую он производит.

Рассмотрим, например, хорошо известную игру с отгадыванием натурального числа от 1 до `n` при помощи вопросов, на которые можно давать ответ "да" или "нет". Количество неопределенностей, которые должен разрешить любой алгоритм для решения этой задачи, можно оценить как `|~log_2 n~|` — количество битов, необходимых для указания конкретного числа из `n` возможных. Каждый вопрос (вернее, ответы на них) можно рассматривать как получение не более одного бита информации о выходе алгоритма (загаданном числе).

Информационно-теоретический подход очень полезен для поиска так называемых информационно-теоретических нижних границ для многих задач с использованием сравнений, включая сортировку и поиск.

Можно доказать, что любой алгоритм, который решает эту задачу, должен в наихудшем случае задать как минимум `|~log_2 n~|` вопросов, если мы сыграем роль соперника, который хочет, чтобы алгоритм задал максимально возможное число вопросов.

После каждого вопроса соперник дает ответ, который оставляет для него наибольшее множество чисел, соответствующих ответам на все ранее заданные вопросы.

Метод соперника для выяснения нижних границ основан на логике злого, но честного противника, который делает все, чтобы алгоритм выполнил как можно больше действий, но честность заставляет его согласовывать свои действия с уже сделанным выбором. В таком случае нижняя граница получается путем измерения количества работы, которая требуется для снижения размера потенциального входного множества до одного элемента по самому длинному пути.

Алгоритмы сортировки и поиска, работают посредством сравнения элементов входных данных. Мы можем изучать производительность таких алгоритмов при помощи дерева принятия решения.

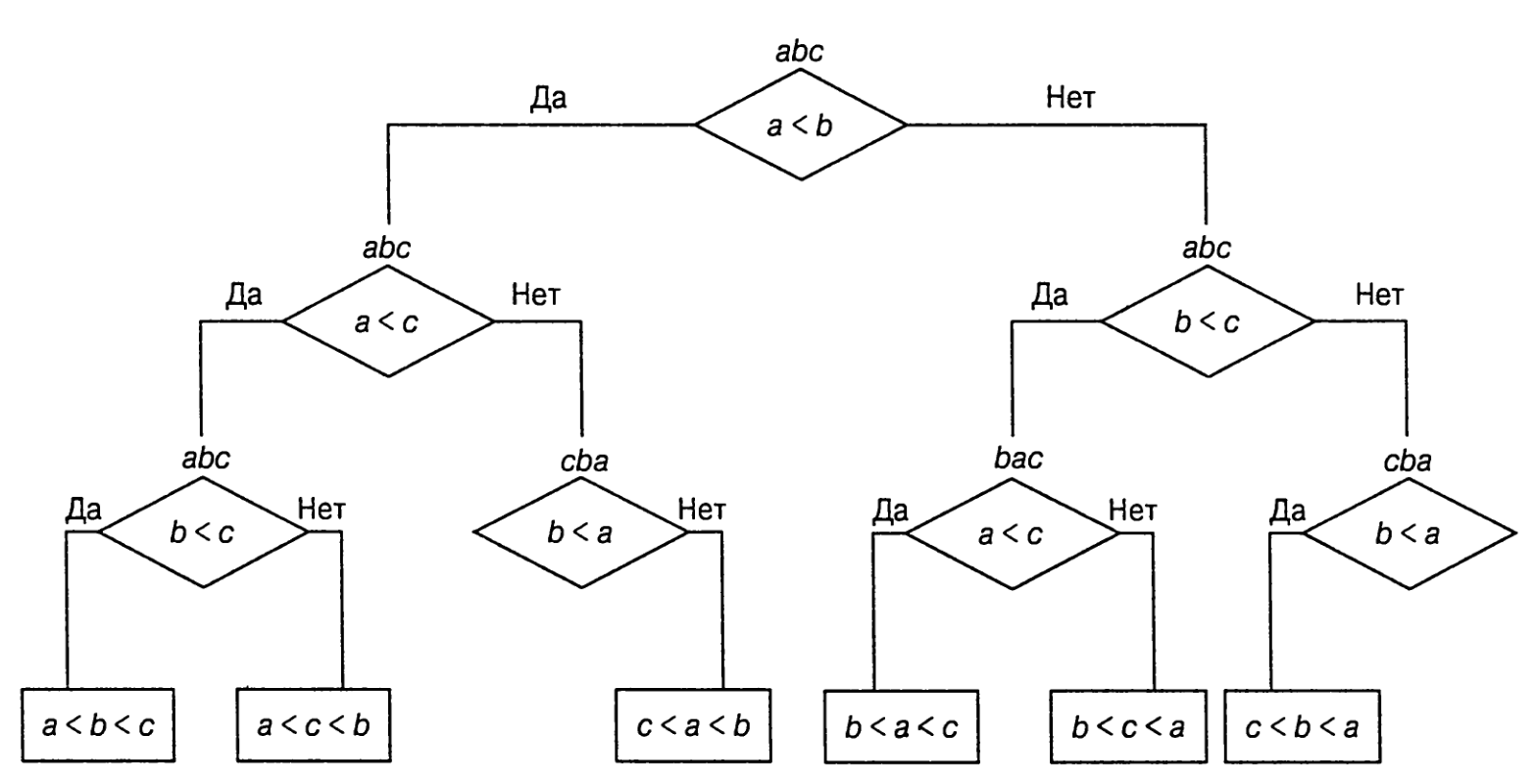
Каждый внутренний узел дерева принятия решения представляет сравнение ключа. Левое поддерево узла содержит информацию о последующих сравнениях, выполняемых, если условие истинно, правое поддерево – если ложно. Например, в задаче поиска минимума из трёх чисел `a, b, c` дерево принятия решения выглядит следующим образом:

Каждый лист представляет возможный выход алгоритма при обработке некоторых входных данных размера `n`.

Количество листьев может оказаться большим, чем количество вариантов выходных данных, поскольку в некоторых алгоритмах один и тот же выход может быть достигнут разными цепочками сравнений. Но количество листьев должно быть не меньше возможных выходных данных.

Работу алгоритма с конкретными входными данными размером п можно представить как проход по пути по дереву принятия решения от корня до листа; количество сравнений при выполнении алгоритма равно количеству ребер на указанном пути.

Следовательно, количество сравнений в наихудшем случае равно высоте дерева принятия решения алгоритма.

Главная идея этого метода заключается в наблюдении, что дерево с данным количеством листьев, которое определяется количеством вариантов выходных данных, должно быть достаточно высоким, чтобы содержать листья в требуемом количестве.

Нетрудно доказать, что для любого бинарного дерева с `n` листьями и высотой `h`

`h >= |~log_2 n ~|`

Максимальное количество листьев в дереве высотой `h` равно `2^h`. Отсюда `2^h >= n`.

Используя неравенство и информационно-теоретический подход можно получить количество сравнений, выполняемых в наихудшем случае любым алгоритмом сортировки и поиска, основанным на сравнениях.

Выход алгоритма сортировки можно рассматривать как поиск перестановки индексов элементов входного списка, которая располагает элементы в возрастающем порядке.

Количество сравнений в наихудшем случае, выполняемое алгоритмом сортировки, не может быть меньше `|~ log_2 n! ~|`.

`C_{"worst"}>=|~ log_2 n! ~| ~~ log_2 sqrt(2 pi n) (n//e)^n in Theta(n log n)`

Отсюда следует плотность асимптотической нижней границы `n log_2 n`, а значит, она не может быть существенно улучшена.

Мы можем также использовать деревья принятия решения и для анализа поведения алгоритма в среднем случае.

Задания для практики

1. Требуется разделить набор из `n` чисел на два части, так чтобы их суммы чисел в этих наборах были равны. Найдите количество возможных решений и информационно-теоретическую нижнюю границу для этой задачи.
2. Рассмотрим задачу определения более легкой фальшивой монеты среди `n` одинаковых по виду монет при помощи рычажных весов. Можем ли мы использовать то же информационно-теоретическое доказательство, что и приведенное в тексте для количества вопросов в игре на отгадывание, чтобы сделать вывод о том, что для определения фальшивой монеты требуется как минимум `|~ log_2 n ~|` взвешиваний в наихудшем случае?