7866.png
ЧЕЛЯБИНСК,ЮУРГУ,ИЕТН

Назад

images/home.png Начало
images/balloon.gif Соревнования
2019

Подразделы

2459. Золотая шахта
2458. Задача торговца
2457. Tower Defence
2456. Генерация персонажа
2455. Секретные уровни
2454. Джокер
2453. Сумма факториалов
2452. Черный монолит
2451. Время для тренировки

Другие разделы

Предварительные результаты регионального этапа олимпиады школьников по информатике в 2018-2019 учебном году

Дата и время

16/11/2024 15:20:03

Авторизация

Имя:
Пароль:
Зарегистрироваться
Восстановить пароль
 

printЗадачи личного первенства ИЕТН по спортивному программированию 2019

printA. Время для тренировки

Ограничения: время – 200ms/500ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Каждое утро Маленький Мук для тренировки пробегает `L` кругов вокруг города. Вдоль дороги на равном расстоянии развешено `N` рекламных плакатов. Во время пробежки Маленький Мук считает, сколько плакатов он пробежал, чтобы знать, какая часть от тренировки им была выполнена.
Помогите Маленькому Муку определить, сколько плакатов должен он должен пробежать, чтобы завершить не менее 10%, не менее 20%, …, не менее 90% от утренней тренировки. Например, если Маленький Мук пробегает 3 круга и на этой дороге 15 плакатов, то после 14-го плаката он выполнит свою тренировку не менее чем на 30% (31.11%)
Первая строка ввода два целых числа – количество кругов `L` и количество плакатов `N` (`1\ ≤\ L,\ N\ ≤\ 10^4`).
Вывести девять целых чисел – сколько плакатов нужно пробежать, чтобы гарантировать, что утренняя тренировка выполнена не менее чем на 10%, 20%, …, 90% соответственно.

Пример ввода

3 15

Пример вывода

5 9 14 18 23 27 32 36 41

printB. Черный монолит

Ограничения: время – 200ms/500ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

41838.png
В джунглях появился большой черный монолит. Мартышка вместо изучения этого феномена хочет просто спрятаться от жаркого солнца, но сначала ей нужно определить, достаточно ли места в тени для отдыха Мартышки и её друзей – Удава, Слонёнка и Попугая.
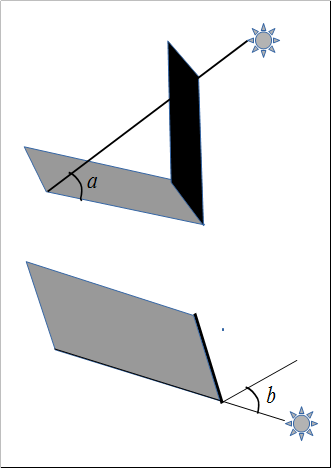
Даны размеры монолита (толщина монолита равна 0), угол `a` между направлением на солнце и поверхностью земли (см. вид сбоку на верхнем рисунке) и угол `b` между направлением на солнце перпендикуляром к грани монолита (см. вид сверху на нижнем рисунке). Вычислите площадь тени от монолита.
41837.png
Первая строка ввода содержит четыре числа – ширина `w` и высота `h` монолита, угол возвышения солнца над горизонтом `a` в градусах и угол между направлением на солнце и перпендикуляром к грани монолита `b` в градусах (`1\ ≤\ w,\ h\ ≤\ 100`, `1\ ≤\ a\ ≤\ 90`, `0\ ≤\ b\ ≤\ 90`).
Вывести одно вещественное число – площадь тени от монолита на земле с абсолютной погрешностью не более `10^{-6}`, если значение площади меньше 10, и относительной погрешностью не более `10^{-8}`, если значение площади больше 10.

Пример ввода 1

1.0 2.5 30.0 0.0

Пример вывода 1

4.330127

Пример ввода 2

1 2 45 45

Пример вывода 2

1.414214

printC. Сумма факториалов

Ограничения: время – 200ms/500ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Факториал `k!` это произведение чисел от 1 до `k`: `k!\ =\ 1*2*…*(k-1)*k`.
Дано некоторое число `N`. Необходимо представить `N` в виде суммы факториалов, например, `10\ =\ 3!\ +\ 2!\ +\ 2!` и `25\ =\ 4!\ +\ 1!`.
Первая строка ввода содержит одно целое числа – `N` (`1\ ≤\ N\ ≤\ 10^5`).
Вывести минимальное количество факториалов, в сумме дающих число `N`.

Пример ввода 1

10

Пример вывода 1

3

Пример ввода 2

25

Пример вывода 2

2

printD. Джокер

Ограничения: время – 500ms/1000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

В игре "Джокер" может участвовать `N` человек (`2\ ≤\ N\ ≤\ 13`). Масть карт в этой игре не важны. Используется колода из 52 карт, достоинство которых обозначается буквами и цифрами A, 2, 3, 4, 5, 6, 7, 8, 9, D, Q, J, K (перечислены в порядке от младших к старшим) и карта с джокером.
Участники садятся по кругу. Участникам раздаются по 4 карты `N` различных достоинств (не обязательно выбранных подряд) и одному из участнику выдается карта с джокером.
Первый ход делает участник, у которого на руках 5 карт, и заключается ход в передаче одной из карт следующему участнику игры по часовой стрелке. Если у участника есть джокер и он получил джокера не на предыдущем ходе (включая первоначальную раздачу), то он передает джокера. Если джокера нет, или джокер был получен ходом ранее, то участник выбирает карту с достоинством, которое у него встречается реже всего. Если таких карт несколько, то он выбирает из них карту с наименьшим достоинством.
Игра заканчивается, когда у одного из участников на руках находится ровно 4 карты и они имеют одинаковое достоинство. Если таких участников несколько (например, после начальной раздачи), то победителем считается участник с меньшим номером.
Определите победителя при заданном распределении карт среди участников.
Первая строка ввода содержит два целых числа – количество участников игры `N` (`2\ ≤\ N\ ≤\ 13`) и номер участника, получившего джокера при раздаче карт `K` (`1\ ≤\ K\ ≤\ N`). Далее следует `N` строк, содержащих по 4 символа из набора A, 2, 3, 4, 5, 6, 7, 8, 9, D, Q, J, K.
Вывести одно целое число – номер участника-победителя.

Пример ввода 1

2 1
3J33
3JJJ

Пример вывода 1

2

Пример ввода 2

2 2
AA22
AA22

Пример вывода 2

2

Пример ввода 3

3 1
JAAQ
AJJJ
AQQQ

Пример вывода 3

3

Пример ввода 4

4 2
477Q
JJ7Q
447Q
4JJQ

Пример вывода 4

3

printE. Секретные уровни

Ограничения: время – 500ms/1000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

В новом платформере несколько уровней, и игрок может выбрать любой из этих уровней для начала игры. На каждом уровне есть основной выход, после попадания в который игра заканчивается, а также может быть несколько секретных переходов на другие уровни.
Дизайнер игры неправильно спроектировал переходы, и опытный игрок может ходить по кругу между несколькими уровнями и набирать бесконечное количество очков.
Для исправления этой проблемы было решено убрать несколько переходов, чтобы таких циклических переходов между несколькими уровнями не было. При этом желательно убрать не более половины переходов, созданных дизайнером.
Первая строка ввода содержит два целых числа – количество уровней `n` (`1\ ≤\ n\ ≤\ 10^5`) и количество переходов `m` (`0\ ≤\ m\ ≤\ 2*10^5`). Далее следует `m` строк, каждая строка содержит два целых числа `u` и `v` (`1\ ≤\ u,\ v\ ≤\ n`), означающие, что на уровне `u` есть переход на уровень `v`. Гарантируется, что нет переходов с уровня на тот же уровень или дублирующих переходов.
В первой строке выведите количество удаляемых переходов `r` (`0\ ≤\ r\ ≤\ m/2`), далее выведите `r` строк, содержащих по одному целому числу `s` (`1\ ≤\ s\ ≤\ m`) – номера удаляемых переходов.
Не нужно минимизировать `r`, достаточно обеспечить, чтобы `r\ ≤\ m/2`. Если существует несколько вариантов решения, выведите любой из этих вариантов.

Пример ввода 1

2 2
1 2
2 1

Пример вывода 1

1
2

Пример ввода 2

3 3
1 2
2 3
3 1

Пример вывода 2

1
1

Пример ввода 3

4 5
1 2
1 3
2 4
3 2
3 4

Пример вывода 3

0

Пример ввода 4

4 5
1 2
2 3
2 4
3 1
4 1

Пример вывода 4

2
4
5

Пример ввода 5

4 3
1 2
2 3
3 4

Пример вывода 5

1
2

printF. Генерация персонажа

Ограничения: время – 500ms/1000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

В новой RPG характеристики персонажа устанавливаются случайно в диапазоне от 1 до `n`. Игрок может перебросить любую характеристику, если её значение ему кажется слишком маленьким, но не более `k` раз. При этом новое значение этой характеристики также выбирается случайно в диапазоне от 1 до `n`.
Петя хочет сгенерировать персонажа с максимально возможным значением некоторой характеристики. Определите математическое ожидание для значения этой характеристики при оптимальной стратегии перебрасывания.
Ввод содержит два целых числа – верхний диапазон для значения характеристики `n` (`1\ ≤\ n\ ≤\ 100`) и максимальное количество перебрасываний характеристики `k` (`1\ ≤\ k\ ≤\ 100`).
Вывести одно число – максимальное математическое ожидание значения характеристики, которой может добиться Петя за не более чем `k` перебрасываний, с точностью `10^{-7}`.

Пример ввода 1

1 1

Пример вывода 1

1.0000000

Пример ввода 2

2 3

Пример вывода 2

1.9375000

Пример ввода 3

6 1

Пример вывода 3

4.2500000

Пример ввода 4

8 9

Пример вывода 4

7.3603358

printG. Tower Defence

Ограничения: время – 2000ms/4000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Для защиты цитадели в точке (0,0) необходимо установить `n` башен на равном расстоянии от цитадели в точках с целочисленными координатами.
Первая строка ввода содержит одно целое число `n` (`1\ ≤\ n\ ≤\ 1000`) – количество башен для защиты цитадели.
В первой строке вывести одно целое число `r` (`1\ ≤\ r\ ≤\ 10^9`) – радиус окружности. Далее вывести `n` строк, каждая строка содержит по два целых числа `x_i`, `y_i` – координаты точек для установки башен (`x_i^2\ +\ y_i^2\ =\ r^2`). Координаты точек должны быть различны. Минимизация радиуса окружности не требуется.

Пример ввода 1

1

Пример вывода 1

100
100 0

Пример ввода 2

7

Пример вывода 2

5
5 0
0 5
-5 0
0 -5
3 4
4 3
-3 -4

printH. Задача торговца

Ограничения: время – 1000ms/2000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Вдоль длинной дороги расположены несколько городов, пронумерованных от 1 до `n`. В каждом городе можно купить или продать некоторый товар. Этот товар имеет большой размер, поэтому торговец может везти с собой не более одной единицы товара. В `i`-м городе товар можно купить за `p_i` золотых, а продать за `(p_i\ -\ 1)` золотых.
Определите максимальную прибыль, которую может получить торговец при путешествии из города `s` в город `t`.
Первая строка ввода содержит одно целое число `n` (`2\ ≤\ n\ ≤\ 10^6`) – количество городов. Вторая строка ввода содержит `n` целых чисел `p_i` в диапазоне от 1 до `10^6` – цена товара в каждом городе. Третья строка ввода содержит одно целое число `m` (`1\ ≤\ m\ ≤\ 10^5`) – количество запросов на вычисление прибыли. Далее следует `n` строк, содержащих по два целых числа `s` и `t` (`1\ ≤\ s,\ t\ ≤\ n`, `s\ ≠\ t`) – номера начального и конечного города путешествия.
Для каждого запроса вывести на соответствующей строке одно целое число – максимальную прибыль, которую может получить торговец при путешествии из города `s` в город `t`.

Пример ввода

7
1 2 7 5 3 10 9
3
1 7
4 7
7 1

Пример вывода

11
6
3

printI. Золотая шахта

Ограничения: время – 2000ms/4000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Питер, используя современные технологии, обнаружил местонахождение нескольких золотых самородков. Чтобы до них добраться, нужно выкопать тоннели либо от входа в шахту, либо от местонахождения какого-то другого самородка. На копание тоннеля необходимо затратить некоторую сумму, которая окупается после продажи найденных самородков.
Напишите программу, которая определит максимальную прибыль Питера и минимальную сумму, которая потребуется на первоначальных этапах для добычи тех самородков, которые обеспечат эту максимальную прибыль.
Первая строка ввода содержит одно целое число `n` (`1\ ≤\ n\ ≤\ 100`) – количество самородков. Далее следует `n` строк, каждая строка содержит три целых числа – номер самородка `p_i`, от которого нужно копать тоннель до `i`-го самородка (`0\ ≤\ p_i\ <\ i`, 0 – вход в шахту), ценность `i`-го самородка `c_i` (`1\ ≤\ c_i\ ≤\ 100`) и стоимость прокладки тоннеля `d_i` (`1\ ≤\ d_i\ ≤\ 100`).
В первой строке вывести два целых числа – максимальная прибыль Питера и минимальная сумма, которая потребуется на первоначальных этапах для получения максимальной прибыли. Если прибыль не нулевая, то во второй строке вывести количество выкопанных самородков, а в третьей строке – порядок выкапывания самородков, обеспечивающий минимум средств, привлекаемых со стороны. Если существует несколько вариантов решения, выведите любой из этих вариантов.

Пример ввода 1

6
0 1 3
1 5 4
1 15 10
0 15 20
4 30 20
5 5 10

Пример вывода 1

9 21
5
4 1 2 3 5

Пример ввода 2

1
0 10 20

Пример вывода 2

0 0
loading