Задачи 2 тура Чемпионата Урала 2003

1. Hyperjump

Ограничения: время – 2s/4s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

In novels "Stars are the cold toys" and "Star shadow" Sergey Lukyanenko described the hyperjump that is a fantastic technology allowing to travel instantly through the space almost without energy loss. Spaceship jumps at the distance of several parsecs (`Theta` constant) and this distance depends neither of the ship’s construction, nor of its mass. The jump direction doesn’t depend from velocity vector of the jump. Direction of the jump is controlled by a human pilot. Without pilot the ship will be taken off to an arbitrary place. Long travels using hyperjump technology are very dangerous, because long series of jumps may put the pilot into hyperspace euphoria so he'll make confused jumps to nowhere until the energy is over.

Ship velocity is controlled by selecting hyperjump direction vector and using additional energy. To change ship velocity by `vec{Delta\ v}` you have to make jump in the direction `vec{Delta\ v}` using additional energy `E={m|Delta\ v|^2}/2`.

Write a program that calculates a series of jumps providing traveling from one point given to another one. The total number of jumps should not be over 30.

Ship velocity in the final point should coincide with the final velocity vector. At the same time, one doesn't have to worry about the minimization of energy consumption for ship velocity changing, because this energy can be taken from the hyperspace during the jump. The distance between the start point and the final one for a single jump should be equal `Theta` constant.

Input

First line of the input file contains 2 real numbers, separated by space; they represent the `Theta` constant (`1\ ≤\ Theta\ ≤\ 20`) and the ship mass `m`, measured in tons (`100\ ≤\ m\ ≤\ 1000`). The next line contains 6 real numbers, separated by spaces; they are ship start point coordinates `(x,\ y,\ z)`, measured in parsecs and vector of ship start velocity `(v_x,\ v_y,\ v_z)`, measured in km/s. The next line also contains 6 real numbers, separated by spaces; they are the final point coordinates, measured in parsecs and the required final velocity vector in km/s. The distance between the start and final points is not exceeded `Theta`. There are following limitations for coordinates and velocities: `|x|≤1000`, `|y|≤1000`, `|z|≤1000`, `|v_x|≤100`, `|v_y|≤100`, `|v_z|≤100`.

Output

The first line of the output file should contain integer `N`, which is the amount of jumps (it is not required to be minimal) for the spaceship travel from the start point to the final one. Each of the next `N` lines of the output file should contain 4 real numbers, separated by spaces: the coordinates (in parsecs, with accuracy `10^{-6}`) of the `i`-th jump destination point and amount of additional energy (in GigaJoules, with accuracy 0.001) to change the ship velocity (`1\ ≤\ i\ ≤\ N`) during this jump. The coordinates of `N`-th point and final point should be equal.

Sample Input

10.0 200.0
0.0 0.0 0.0 –5.0 0.0 0.0
20.0 10.0 0.0 0.0 2.0 3.0

Sample Output

5
10.000000 0.000000 0.000000 0.000
20.000000 0.000000 0.000000 2500.000
20.000000 10.000000 0.000000 400.000
20.000000 10.000000 10.000000 900.000
20.000000 10.000000 0.000000 0.000

Условие задачи на русском языке

2. Monotonic Subsequence

Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Let us consider some permutation of numbers from 1 to 10, for example (10, 1, 8, 3, 4, 7, 5, 6, 2, 9). The longest increasing subsequence is (1, 3, 4, 5, 6, 9). Its length equals 6. The longest decreasing subsequence is (10, 8, 7, 5, 2). Its length equals 5. So, the length of the most long monotonic (increasing or decreasing) subsequence equals 6.

Your program must find permutation of numbers from 1 to `N` with minimal length of the longest monotonic subsequence, where `N` is a given integer number.

Input

The first line of the input file contains single integer `N` (`1\ ≤\ N\ ≤\ 1000`).

Output

Write into the first line of the output file the number, which is equal to minimal length of the longest monotonic subsequence of permutation of numbers from 1 to `N`. The second line of the output file should contain such permutation `(a_1,\ a_2,\ …,\ a_N)` with mentioned property, that gives the minimal value of expression `a_1*N^{N–1}+a_2*N^{N–2}+…+a_{N–1}*N+a_N`, i.e. the first permutation in lexicographic order with mentioned property. The elements of permutation would be separated by one space.

Sample Input

Sample Output

3
3 2 1 6 5 4 9 8 7

3. Collection of Postage Stamps

Ограничения: время – 300ms/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Bob collects postage stamps. Every stamp has not only a nice picture, but also a number, which is nominal cost. Once Bob decided to count how many different sums may be composed from his stamps, but after some thousands variants he lost his way. He needs your help badly!

Write the program for calculation of the quantity of different sums, which may be composed from Bob’s stamps.

Input

The first line of the input file contains an integer `N\ (1≤N≤1000)`, which is equal to the amount of Bob’s stamps. The following `N` lines contain the nominal costs of Bob’s stamps (a single integer from 1 to 1000 in a line).

Output

Write into the output file the quantity of different sums, which may be composed from stamps of given nominal costs.

Sample of input

Output for the sample input

4. Glutton

Ограничения: время – 2s/4s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

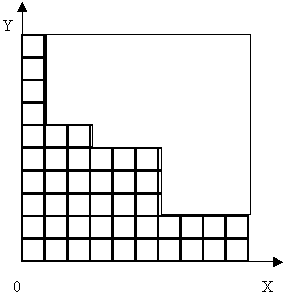
Alex and Bob divide a pie, cutting its pieces in turn. The pie is square-shaped and separated by 9 horizontal and 9 vertical lines of icing into 100 squares. The action of each player is as follows. He chooses one of the squares of pie’s remainder and takes it and all squares to the right and above (for this he leads the cuts from the left and bottom vertex of this square to the right and up; in case of square’s disposition in the lowest row or in the most left column only one cut is needed). The looser is that player who takes the last square, which is the most left and the lowest. He is a glutton!

Write the program, which analyzes the sequence executed moves and gives recommendation for the player making the next move.

Input

The first line of the input file contains an integer `N\ (0\ ≤\ N\ <\ 100)`, which equals the amount of moves made in the game. The following N lines contain pairs of integers `x_i\ y_i\ (0\ ≤\ x_i\ <\ 10,\ 0\ ≤\ y_i\ <\ 10,\ x_i+y_i\ ≠\ 0)`, separated by space; each pair presents coordinates of point used by player for cutting the part of the pie.

Output

Write into the output file two integers, separated by space, which are the coordinates of the point for the best move (this move guaranties the win in case of faultless following game of players). Write any (one) variant of winning move. If there is no winning move, write 0 0 (two zeroes) to the output.

Sample #1 of input (see picture)

Output for the sample #1

1 1

Sample #2 of input

1
1 1

Output for the sample #2

0 0

5. Sawing the Beam

Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Bob wants to saw the beam (rectangular parallelepiped with integer length, width and height) to get unit cubes. He wants to minimize the number of cuttings, putting several parts of the beam together so, that one cutting may separate them simultaneously.

Write the program, which for given length, width and height calculates the minimal amount of cuttings needed for partition of the beam into unit cubes.

Input

First line of the input file contains 3 integers (from 1 to 1000), separated by the space; they represent length, width and height of the beam.

Output

On the first line of the output file write minimal amount of cuttings.

Sample Input #1

3 3 3

Sample Output #1

Sample Input #2

4 4 4

Sample Output #2

6. The Run

Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Bob is a coach of juniors' baseball team. One day he ordered team to run around the playing-field five times. Soon he was distracted by telephone call. While Bob and Alex discussed the plans of big party, the run was ended. Bob asked several children about the results of the run. But nobody of them can give him the order how they came to finish. Children remembered only who were before him and who were after him. Children did not remember exact order among they also. Probably somebody was mistaken, because Bob could not determine the order how children came to finish by the results of interview.

Write the program to help Bob to determine who was wrong in his evidence.

Input

The first line of the input file contains an integer `N` (`1\ ≤\ N\ ≤\ 100`), which equals the amount of the participants of the run, who gave their evidence to Bob. The following `N` lines contain several integers separated by spaces. The first integer in a line is the number of the participant who gave his evidence. The numbers of participants who gave evidence are different. Further there are numbers of those participants who finished before him, then 0 (zero), then the numbers of those participants who finished after him, then 0 (zero). The numbers of all participants are written at their game shirts and have values from 1 to 100.

Output

Write into the output file 0 (zero), if there are no contradictions in these evidences. If there are contradictions and they can be explained by errors of single participant, write the numbers of participants who may be mistaken in increasing order. The numbers should be separated by one space. If there are contradictions and they cannot be explained by single error evidence, write the number `–1`.

Sample Input #1

1
2 1 0 3 0

Sample Output #1

Sample Input #2

Sample Output #2

1 2

Sample Input #3

3
2 1 0 3 0
1 3 0 2 0
3 2 0 1 4 0

Sample Output #3

-1

Clarification
Children finished at different time.
Условие задачи на русском языке

7. Transformation of the Graph

Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Let find the path going through all the vertices of the oriented graph one time, i.e. find Hamiltonian path. This problem belongs to the class of NP-hard problems, and its straightforward solution needs many hours of calculations. Sometimes it's possible to build new graph G', which contains as mush arcs, as many vertices are in source graph `G`, and there is bijection `φ` (one-to-one correspondence) between the set of the vertices of `G` and the set of the arcs of `G'` such that if there is an arc `(x\ y)` in `G`, where `x≠y`, then the end of the arc `φ(x)` in `G'` coincides with the beginning of the arc `φ(y)`. The bijection `φ` maps adjacent vertices in `G` to adjacent arcs in `G'` and nonadjacent vertices in `G` to nonadjacent arcs in `G'`. In this case the problem of finding Hamiltonian path in source graph reduces to the problem of finding Eulerian path in new graph, the last one is much easier. The self-adjacency of vertices in the source graph and arcs in the new graph should not be taken into account, as it has not effect to path searching.

Write the program, which checks the possibility of mentioned transformation for given oriented graph and build new oriented graph.

Input

The first line of the input file contains two integers `K` and `N` (`1\ ≤\ K\ ≤\ 100`, `1\ ≤\ N\ ≤\ K^2`), separated by space, where `K` is quantity of vertices and `N` is quantity of arcs of source graph `G`. The following `N` lines contain pairs of integers from 1 to `K`, separated by space; each pair describes the beginning and the end of an arc.

Output

The output file contains zero in case of impossibility of mentioned transformation. Else the first line contains the quantity `M` of vertices of new graph and the following `K` lines contain information about arcs of new graph; you should write in `i`-th line the numbers of beginning and end of `i`-th arc, which corresponds to `i`-th vertex of source graph. Use arbitrary indexing from 1 up to `M` for vertices of new graph.

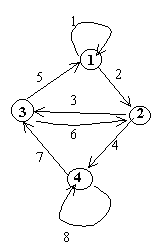
Sample Input #1

Sample Output #1

Sample Input #2

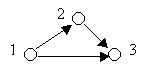
Sample Output #2

8. Commissions

Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (2)

There are some commissions in the parliament. Each deputy may be a member of some commissions, in particular neither of them. The chairman of the every commission is its member. Nobody of deputies can be chairman of more than one commission simultaneously.

In the result of regular election the membership of parliament is not changed. The commissions were reformed. It’s interesting, that all old chairmen became chairmen again, but maybe of other commissions.

Write the program, which determines the chairmen of commissions based on the staff of commissions of old and new parliaments.

Input

The first line of the input file contains two integers `N` and `K` (`2\ ≤\ N\ ≤\ 100`, `1\ ≤\ K\ ≤\ N/2`), separated by space, where `N` is the quantity of deputies in parliament and `K` is the quantity of commissions. The following `K` lines describe the staff of old commissions. `i`-th line contains an integer `P_i` (`1\ ≤\ P_i\ ≤\ N`), which is equal to the amount of members of `i`-th commission, and then `P_i` numbers of them. All integers are separated by spaces. The next `K` lines describe new commissions similarly.

Output

Write into the output file `K` lines; `i`-th line has to contain two integers, where the first one is the number of new `i`-th commission's chairman, and the second one is the number of commission in old parliament, where he was chairman. If there are some such variants of chairs distribution, you should output one of them.

Sample Input

6 3
3 1 2 3
2 4 5
2 5 3
1 5
5 4 5 6 1 2
2 6 2

Sample Output

5 3
4 2
2 1

25/04/2003	7-й Чемпионат Урала. 2 тур (1)
03/10/2007	Занятие 4 (C)
14/03/2009	Занятие 15 (G)
08/07/2013	Лето 2013-5 (A)

25/04/2003	7-й Чемпионат Урала. 2 тур (2)
08/07/2013	Лето 2013-5 (B)

25/04/2003	7-й Чемпионат Урала. 2 тур (3)
03/07/2006	Лето 2006 дорешивание ( 1D)
03/07/2006	Лето 2006 - 1 (D)
08/07/2013	Лето 2013-5 (C)
05/10/2023	Занятие 1 (проводит test2) (A)
11/10/2023	Занятие 2 (проводит test2) (A)

25/04/2003	7-й Чемпионат Урала. 2 тур (4)
05/10/2006	Практическое занятие 4 (E)
27/09/2008	Занятие 3 (E)
08/07/2013	Лето 2013-5 (D)

25/04/2003	7-й Чемпионат Урала. 2 тур (5)
08/07/2013	Лето 2013-5 (E)
04/07/2018	Лето 2018 - 5 (упрощенное) (A)
08/07/2020	Лето 2020 - 4 (упрощенное) (A)

Назад

Подразделы

Другие разделы

Дата и время

Авторизация

Задачи 2 тура Чемпионата Урала 2003

1. Hyperjump

2. Monotonic Subsequence

3. Collection of Postage Stamps

4. Glutton

5. Sawing the Beam

6. The Run

7. Transformation of the Graph

8. Commissions