Разбор задач отборочных командных соревнований школьников 2012

Разбор задачи A. Расстояния в Плоском мире

Тема: реализация программы по заданному алгоритму
Сложность: простая

Алгоритм программы указан в условии задачи. Абсолютное значение (модуль) числа в языке Pascal можно вычислить с помощью функции abs.

var x1,y1,x2,y2:integer;
begin
  read(x1,y1,x2,y2);
  if y1=y2 then
    writeln(abs(x1-x2))
  else
    writeln(abs(x1)+abs(x2)+abs(y1-y2));
end.

Если функцию abs не использовать, то программа будет более сложной:

var x1,y1,x2,y2,r:integer;
begin
  read(x1,y1,x2,y2);
  if y1=y2 then
  begin
    r:=x1-x2;
    if r<0 then
      r:=-r;
  end
  else
  begin
    r:=y1-y2;
    if r<0 then
      r:=-r;
    if x1<0 then
      x1:=-x1;
    if x2<0 then
      x2:=-x2;
    r:=r+x1+x2;
  end;
  writeln(r);
end.

Разбор задачи H. Новая столешница

Тема: геометрия
Сложность: простая

Для решения задачи проще всего использовать формулу Герона:

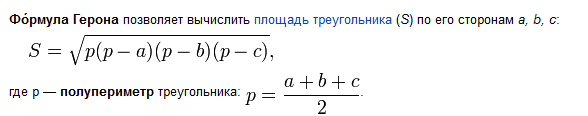
Зная площадь столешницы `S`, можно найти её минимальный боковой размер – высоту: `h_c=2S/C`. И остается только сравнить высоту столешницы с диагональю прямоугольного проёма, которую можно вычислить по теореме Пифагора: `d^2=W^2\ +\ H^2`. Можно не вычислять корни, а сравнить квадраты высоты `h_c` и диагонали `d` (так как функция корня является монотонно возрастающей), и даже обойтись без сравнения дробных чисел, домножив обе части неравенства на знаменатель (так как знаменатель положительный).

var a,b,c,w,h:int64;
begin
  read(a,b,c);
  read(w,h);
  if (a+b+c)*(a+b-c)*(a-b+c)*(-a+b+c)<=4*c*c*(w*w+h*h) then
    writeln('YES')
  else
    writeln('NO');
end.

Разбор задачи E. Определение победителя

Тема: обработка строк, редукция
Сложность: простая

Так как для каждой строки ввода нужно выполнить одинаковые преобразования в баллы и суммирование, удобно оформить это действие в виде подпрограммы:

procedure readncalc(var r:integer);
var i:integer;
    s:string;
begin
  r:=0;
  readln(s);
  for i:=1 to length(s) do
    if s[i]='J' then r:=r+3 { удар Jab - 3 балла }
    else if s[i]='K' then r:=r+2 { удар Kick - 2 балла }
    else r:=r+1; { остальные удары - 1 балл }
end;

Остальная часть программы выглядит после этого очень просто:

var r1,r2:integer;
begin
  readncalc(r1); { Ввод и расчет баллов для каждого участника }
  readncalc(r2);
  if r1>r2 then writeln(1) { Сравнение и вывод победителя }
  else if r1<r2 then writeln(2)
  else writeln(0);
end.

Разбор задачи D. Соревнования

Тема: полный перебор
Сложность: ниже среднего

Перебираем все варианты количества человек в первой команде `A` от `N` до 1. Для количества гномов `B` есть два ограничения: 1) `B\ ≤\ A`; 2) `B*A\ ≤\ N`, т.е. `B\ ≤\ N/A`. Поэтому нужно рассматривать варианты количества гномов в диапазоне от `min(A,N/A)` до 1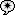. Количество троллей `C` для выбранных `A` и `B` определяется однозначно из формулы `A*B\ +\ A*C\ +\ B*C\ =\ N`: `C\ =\ (N\ -\ A*B)/(A+B)`, при этом 1) `C` должно быть целым числом и 2) `C\ ≤\ B`.
Оценка времени работы алгоритмы равна `O(N*sqrt(N))`.

var a,b,c,bn,n:longint;
begin
  read(n);
  for a:=n downto 1 do
  begin
    bn:=n div a;
    if bn>a then bn:=a;
    for b:=bn downto 1 do
    begin
      c:=(n-b*a) div (a+b);
      if (c<=b) and (a*b+b*c+a*c=n) then
        writeln(a,' ',b,' ',c);
    end;
  end;
end.

Разбор задачи F. Лгуны и правдолюбы

Тема: задача на идею, логику
Сложность: ниже среднего

Пусть кто-то из героев назвал число `k`. Если этот герой является правдолюбом, то `k` героев (лгуны) должны назвать число, не совпадающее с `k`, а остальные `n-k` героев должны также сказать число `k`. Поэтому нужно подсчитать сколько раз названо каждое число `k` (для всех `k` от 0 до `n`). Если оно названо ровно `n-k` раз, то это один из вариантов количества лгунов в компании.

var sum:array[0..100] of integer;
    n,k,kv:integer;
begin
  read(n);
  { Считаем количество героев, сказавших некоторое число }
  for i:=1 to n do 
  begin
    read(k);
    inc(sum[k]);
  end;
  { Считаем количество вариантов }
  kv:=0; 
  for k:=0 to n do
    if sum[k]=n-k then
      inc(kv);
  { Выводим варианты }
  writeln(kv);
  if kv>0 then
  begin
    for k:=0 to n do
      if sum[k]=n-k then
        write(' ',k);
    writeln;
  end;
end.

Разбор задачи B. Великий пожар Анк-Морпорка

Тема: поиск в ширину
Сложность: средняя

Для решения задачи необходимо использовать известный алгоритм поиска в ширину. Для лучшего понимания алгоритма рекомендуется рассмотреть разбор задач 741. Ход конем и 1509. Очистка озера.

Дополнительно можно воспользоваться следующими оптимизациями: 1) окружить поле клетками с '.'; 2) свести задачу к одному измерению (т.е. текущее состояние будет описываться одним целым числом).
Объявление необходимых структур данных:

var n,m:integer; { размеры карты }
  map:array [0..52*52] of char; { карта }
  q:array [0..50*50] of integer; { очередь } 
  q1,q2:integer; { индекс начала и конца очереди }
  step:array [0..52*52] of integer; { информация о времени возгорания, -1 означает, что дом не горел }
  maxkol,maxr,maxc, { наилучший результат и координаты дома для поджога }
  curstep,newstep, { текущее время и время возгорания следующего дома }
  qpos0,qpos1,qpos2, { начальные позиции в очереди для предыдущего, текущего и нового времени возгорания }
  i,j,p,pn:integer; {вспомогательные переменные }

Первая часть программы – ввод данных. Двумерная карта города размером `(n+2)\ times\ (m+2)` хранится в одномерном массиве последовательно по строкам. Ячейка с координатами `(i,j)` в одномерном массиве имеет индекс `i*(m+2)+j`. Строки карты с номерами 0 и `n+1` и столбцы с номерами 0 и `m+1` заполняются символами '.'.

  readln(n,m);
  for j:=0 to m+1 do
    map[j]:='.';
  for i:=1 to n do
  begin
    map[i*(m+2)]:='.';
    for j:=1 to m do
      read(map[i*(m+2)+j]);
    map[i*(m+2)+m+1]:='.';
    readln;
  end;
  for j:=0 to m+1 do
    map[(n+1)*(m+2)+j]:='.';

Далее перебираем все варианты, какой дом будет подожжен первым, и выполняем поиск в ширину. При изменении времени возгорания смещаем позиции указателей qpos0, qpos1, qpos2 в очереди и проверяем на увеличение текущего максимума одновременно горящих домов.

  maxkol:=0;
  for i:=1 to n do
    for j:=1 to m do
    begin
      p:=i*(m+2)+j; { выбираем клетку (i,j) }
      if map[p]='#' then { если там есть дом }
      begin
        for pn:=0 to (n+2)*(m+2)-1 do { очищаем массив времени возгорания }
          step[pn]:=-1;
        step[p]:=0; { дом в клетке (i,j) загорается в момент 0 }
        q[0]:=p; { помещаем его в очередь }
        q1:=0;q2:=1;
        curstep:=0;
        qpos0:=0;
        qpos1:=0;
        qpos2:=0;
        while q1<q2 do { очередь не пуста }
        begin
          p:=q[q1];
          inc(q1);
          newstep:=step[p]+1; { новое время }
          if newstep>curstep then { время изменилось }
          begin
            qpos0:=qpos1; {  сдвигаем указатели }
            qpos1:=qpos2;
            qpos2:=q2;
            curstep:=newstep;
            if qpos2-qpos0>maxkol then { найден новый максимум }
            begin
              maxkol:=qpos2-qpos0; { запоминаем }
              maxr:=i;
              maxc:=j;
            end;
          end;
          fire(p+1); { поджигаем все соседние дома }
          fire(p-1);
          fire(p+m+1);
          fire(p+m+2);
          fire(p+m+3);
          fire(p-m-1);
          fire(p-m-2);
          fire(p-m-3);
        end;
      end;
    end;

Подпрограмма fire выглядит следующим образом:

procedure fire(p:integer);
begin
  if (map[p]='#') and (step[p]=-1) then { в позиции p есть дом, который еще не горел }
  begin
    step[p]:=newstep; { отмечаем время возгорания }
    q[q2]:=p; { добавляем дом в очередь }
    inc(q2);
  end;
end;

В завершающей части программ выводится найденный максимум и координаты дома.

  writeln(maxkol);
  writeln(maxr,' ',maxc);

Другим способом ускорения работы своей программы является выключение проверок на выход за границы массива и переполнение, включенных по умолчанию при компиляции – см. опции компилятора на странице Помощь. Для этого в начале программы нужно дописать комментарий:

{$R-} {$Q-} {$S-}

Следует отметить, что на первоначальных этапах разработки эти проверки являются достаточно важными и дают дополнительную информацию для исправления ошибок в программе. Ошибка времени исполнения (RT) часто сигнализирует о неправильно выбранном диапазоне для цикла или неправильно выбранном типе данных (integer вместо longint или int64). При выключении проверок ошибка типа RT превращается в WA или PE, которые обычно сигнализируют о нерассмотренном случае или неверной формуле.
Рекомендуется выключать проверки только при получении TL, и такое выключение сможет помочь только в случае, если реализованный алгоритм решения задачи требует существенно меньше `10^9` операций. Иначе нужно изменять алгоритм.

Разбор задачи I. Переправа

Тема: динамическое программирование
Сложность: средняя

В большинство соревнований есть задача на использование метода динамического программирования. На сайте есть большой набор задач на эту тему.

Сначала определим необходимые структуры данных:

var n,m, { количество типов лодок и грузов }
    i,j, { вспомогательные переменные }
    k, { количество погруженных в лодку грузов }
    sumw:longint; { вес грузов, помещенных в очередную лодку }
    dt:array[0..100000] of record dif,tip,prd,kol:longint; end; 
       { таблица для динамического программирования: минимальный недогруз, 
         тип использованной лодки, начиная с какого груза в очереди, 
         количество лодок }
    w:array[1..100000] of integer; { вес грузов в очереди }
    g:array[1..50] of integer; { грузоподъемность лодок }

В первой части программы выполняется ввод и инициализация массивов:

  read(n,m);
  for i:=1 to n do
    read(g[i]);
  for i:=1 to m do
    read(w[i]);
  for i:=1 to m do
    dt[i].dif:=1000000000; { бесконечность }
  dt[0].dif:=0; { для 0 грузов недогруз равен 0 }
  dt[0].kol:=0;

Далее основной цикл по заполнению таблицы. Если известен минимальный недогруз для `i-1` груза, то, перебрав все типы лодок, можно получить минимальный недогруз для следующей партии грузов.

  for i:=1 to m do
  begin
    k:=0;
    sumw:=0;
    for j:=1 to n do
    begin
      while (i+k<=m) { есть грузы в очереди }
        and (sumw+w[i+k]<=g[j]) do { и их суммарный вес не превышает 
                                   грузоподъемности лодки j-го типа }
      begin
        sumw:=sumw+w[i+k];
        inc(k);
      end;
      { в лодку j-го типа загрузили k-1 груз, начиная с i-го, весом sumw }
      { последний загруженный в лодку груз имеет номер i+k-1 }
      { недогруз составляет g[j]-sumw }
      { минимальный недогруз для предыдущего груза в dt[i-1].dif }
      if dt[i-1].dif+g[j]-sumw<dt[i+k-1].dif then { если результат улучшился }
      begin
        dt[i+k-1].dif:=dt[i-1].dif+g[j]-sumw; { запоминаем }
        dt[i+k-1].tip:=j;
        dt[i+k-1].prd:=i-1;
        dt[i+k-1].kol:=dt[i-1].kol+1;
      end;
    end;
  end;

И наконец выводим результат.

  writeln(dt[m].kol,' ',dt[m].dif);
  print(m);
  writeln;

Для вывода списка типов лодок в обратном порядке здесь используется рекурсивная подпрограмма:

procedure print(i:integer);
begin
  if i=0 then exit;
  print(dt[i].prd); { сначала выводим предыдущие значения }
  write(' ',dt[i].tip); { затем тип последней использованной лодки }
end;

Разбор задачи C. Проверка на сообразительность

Тема: нахождение наидлиннейшей возрастающей подпоследовательности, сортировка, бинарный поиск
Сложность: средняя

С первого взгляда кажется это известная задача на поиск наибольшей общей подпоследовательности (LCS), которая решается за время `O(N*M)`, но фраза "В каждой из последовательностей все числа попарно различны" упрощает задачу. Так как каждый элемент второй последовательно встречается не более одного раза в первой последовательности, то выписав последовательность номеров, под которым элемент из второй последовательности идет в первой последовательности (только для общих элементов последовательностей), мы сведем задачу к поиску наидлиннейшей возрастающей подпоследовательности, который выполняется за `O(N*log(N))`.
Подробное изложение этого алгоритма можно посмотреть на сайте e-maxx.ru

int d[MAXN];
k=0;
for (int i=0; i<n; i++) {
	int j = int (lower_bound (d, d+k, a[i]) - d);
        if(j==k)
           d[k++]=a[i];
        else	if (a[i] < d[j])
	  d[j] = a[i];
}

Для ускорения поиска элементов в первой последовательности необходимо использовать map или быструю сортировку (см. разбор задачи 1692. Шпаги) и бинарный поиск в получившейся упорядоченной последовательности (см. разбор задачи 1366. Дипломы).

Разбор задачи G. Взаиморасчеты

Тема: задача на идею, поиск инварианта
Сложность: сложная

В основу задачи положена задача M1258 из журнала Квант №12 за 1990г. (автор задачи О. Ижболдин).
Разбор решения задачи был опубликован в №12 за 1991г.

Для сведения задачи к рассмотренной в журнале и для избавления от дробных чисел выполним замену `a'_i=(a_i-S)*N`, где `S` – среднее арифметическое чисел `a_i`.
Среднее станет равным 0 и результат операции обмена будет иметь вид `a_{(i-1)\ mod\ N}+a_i,\ -a_i,\ a_{(i+1)\ mod\ N}+a_i`. При рассмотрении частичных сумм `b_i=∑_{j=0..i}\ a_j` можно обнаружить, что операция сводится к обмену значений `b_{i-1}` и `b_i`.
Таким образом, получение конечного распределения возможно, если последовательность частичных сумм для конечного распределения состоит из перемешанных произвольным образом чисел `b_i+d`, где `d` – некоторая константа, совпадающая с одним из `b_i` (при обмене с 1 человеком происходит сдвиг `b_i` по кругу). Константу легко найти с помощью сортировки частичных сумм для начального и конечного распределения.
Затем нужно привести последовательность частичных сумм для начального распределения в соответствие с последовательностью частичных сумм для конечного распределения с помощью обменов (аналог сортировки пузырьком).
Время работы алгоритма `O(N^2)`.