Подразделы
Другие разделы
| 1659. Раскраска в три цвета |
| 1660. Эльфы и олени |
| 1661. Эксперимент |
| 1662. Шоссе |
| 1663. Автомобильные номера |
| 1664. Планета Плюк |
| 1665. Полигон |
| 1667. Изображение таблицы |
| 1668. Неправильная считалка |
Дата и время
28/02/2026 00:48:43
 1666. Красно-черные деревья
1666. Красно-черные деревья
 Красно-черные деревья
Красно-черные деревья
 Динамическое программирование и запоминающие функции
Динамическое программирование и запоминающие функцииОлимпиадные задачи на русском языке

| 04/07/2011 | Лето 2011 - дорешивание (15H) |
| 22/07/2011 | Лето 2011 - 15 (H) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Широкое распространение в стандартных библиотеках многих языков
программирования получила реализация сбалансированных деревьев
на основе так называемых красно-черных деревьев. В данной задаче
вам предлагается посчитать количество красно-черных деревьев
заданной формы.
Напомним, что двоичным деревом называется набор вершин, организованных
в виде дерева. Каждая вершина имеет не более двух детей, один из
которых называется левым, а другой — правым. Как левый,
так и правый ребенок, а также оба могут отсутствовать.
Если вершина `Y` — ребенок вершины `X`, то говорят, что
вершина `X` является родителем
вершины `Y`. У каждой вершины дерева, кроме одной, есть ровно один родитель.
Единственная вершина, не имеющая родителя, называется корнем дерева.
Соединим каждую вершину кроме корня с ее родителем. Заметим, что
для каждой вершины существует ровно один путь, ведущий в нее от корня.
Двоичное дерево называется красно-черным, если каждая его вершина
раскрашена в красный либо в черный цвет, причем выполняются следующие условия:
- если вершина красная, то ее родитель — черный;
- количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.
Примеры двоичного дерева, вершины которого раскрашены в два цвета,
приведены на следующем рисунке.
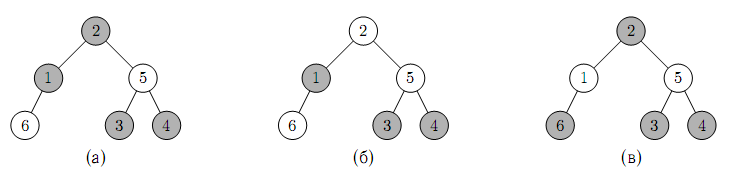
Если считать закрашенные
вершины черными, а незакрашенные — красными, то дерево на рисунке (а)
является красно-черным деревом, а деревья на рисунках (б) и (в) — нет.
Для дерева на рисунке (б) нарушается первое свойство — у красной вершины 5
родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство —
на пути от корня до вершины 1 одна черная вершина, а, например, на
пути от корня до вершины 3 — две.
Для заданного двоичного дерева подсчитайте число способов раскрасить
его вершины в черный и красный цвет так, чтобы оно стало красно-черным
деревом.
Ввод
Первая строка входного файла содержит число `n` — количество вершин в дереве
(`1\ ≤\ n\ ≤\ 1000`).
Пусть вершины дерева пронумерованы числами от `1` до `n`.
Следующие `n` строк содержат по два числа — для каждой вершины заданы
номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо
его номера записан ноль. Гарантируется, что входные данные корректны, то
есть набор чисел во входном файле действительно задает двоичное дерево.
Вывод
Выведите в выходной файл одно число — количество способов раскрасить вершины
заданного во входном файле двоичного дерева в красный и черный цвета так,
чтобы оно стало красно-черным деревом.
Пример ввода 1
6 6 0 1 5 0 0 0 0 3 4 0 0
Пример вывода 1
3
Пример ввода 2
4 2 0 3 0 4 0 0 0
Пример вывода 2
0

Источник: VI Всероссийская командная олимпиада школьников по программированию, 2005

 Начало
Начало