Решение

Тема: динамическое программирование
Сложность: высокая

Вычисление производится методом динамического программирования. Элемент матрицы `T[i,j]` содержит минимальную стоимость для проведения дороги в позицию после `i`-го участка горного рельефа на высоту `j`. `T[0,j]` вычисляется как `j^2*C_2/2`, так как попасть на высоту `j` можно только построив насыпь.

При вычислении `T[i,j]` возможны три случая.

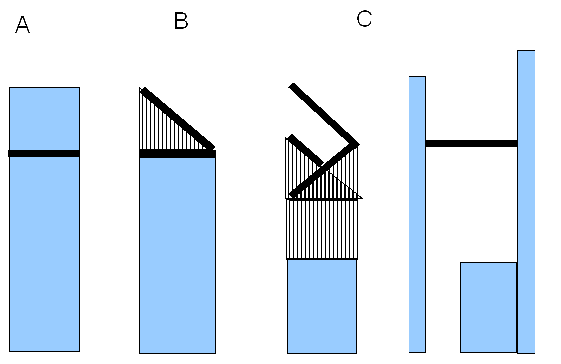
A. Если высота `i`-го участка рельефа выше `j`, то попасть в эту точку можно только с помощью прокладки туннеля: `T[i,j]=T[i-1,j]+C_1`.

B. Если высота `i`-го участка рельефа равна `j`, то попасть в эту точку можно либо проведя дорогу по поверхности горы, либо построив наклонную насыпь с большей высоты: `T[i,j]=min(T[i-1,j],T[i-1,j+1]+C_2/2)`.

C. Если высота `i`-го участка рельефа меньше `j`, то попасть в эту точку можно либо построив наклонную насыпь с большей или меньшей высоты, либо построив v-образную дорогу (насыпать дорогу горизонтально нет смысла), либо построить мост, если возможно (далее на высоте j должна быть скала для правой опоры моста, и не более чем в 3 единицах должна быть скала для левой опоры моста). `T[i,j]=min(\ min(T[i-1,j]-C_2/4,T[i-1,j+1]+C_2/2,T[i-1,j-1]-C_2/2)\ +\ (j-h[i])*C_2,\ "вариант"\ с\ "мостом")`.

После заполнения матрицы нужно найти минимум среди значений `T[n,j]+\ j^2*C_2/2`.

var N,i,j,k,c1,c2,c3:integer;
  h:array[1..1000] of integer;
  t:array[0..1000,0..1000] of extended;
  r:extended;
procedure setmin(v:extended);
begin
  if v<t[i,j] then t[i,j]:=v;
end;
begin
  read(n,c1,c2,c3);
  for i:=1 to n do
    read(h[i]);
  for j:=0 to 1000 do
    t[0,j]:=j*j/2*c2;
  for i:=1 to n do
    for j:=0 to 1000 do
    begin
      if h[i]>j then
        t[i,j]:=t[i-1,j]+c1
      else if h[i]=j then
      begin
        t[i,j]:=t[i-1,j];
        if j<1000 then setmin(t[i-1,j+1]+c2/2);
      end
      else
      begin
        t[i,j]:=t[i-1,j]+(j-h[i])*c2-c2/4;
        if j<1000 then setmin(t[i-1,j+1]+(j-h[i])*c2+c2/2);
        setmin(t[i-1,j-1]+(j-h[i])*c2-c2/2);
        if (i<n) and (h[i+1]>=j) then
        begin
          for k:=1 to 3 do
            if (i>k) and (h[i-k]>=j) then
            begin
              setmin(t[i-k,j]+k*c3);
              break;
            end;
        end;
      end;
    end;
  r:=t[n,0];
  for j:=1 to 1000 do
    if r>t[n,j]+j*j/2*c2 then
      r:=t[n,j]+j*j/2*c2;
  writeln(r:1:2);
end.