 Задачи районно-городских командных соревнований 2003
Задачи районно-городских командных соревнований 2003
1. Безумное чаепитие
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
`N` участников "безумного чаепития" сидят вокруг стола. Каждую минуту одна пара соседей по столу может
поменяться местами. Найти минимальное время (в минутах) необходимое для того, чтобы все участники чаепития
пересели в обратном порядке (т.е. левый сосед должен стать правым, а правый – левым).
Во входном файле в первой строке содержится количество тестов. Каждая следующая строка содержит одно
целое число `N` (`1\ ≤\ N\ ≤\ 32767`) – количество участников безумного чаепития.
В выходной файл вывести на отдельной строке для каждого числа `N` минимальное время, требуемое для пересадки
всех `N` участников.
Источник: ACM ICPC SEERC 2003
2. Похититель глины
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Миссис Терри – учитель рисования в детском саду – любит, когда ее дети лепят что-нибудь из глины.
Одно из ее заданий заключается в том, чтобы придать куску глины форму прямоугольного бруска и измерить его стороны.
Однако в каждой группе всегда находится один ребенок, который норовит отобрать немного глины у товарища.
Поскольку миссис Терри всегда выдает всем детям равные куски глины, вы можете написать программу,
которая поможет миссис Терри найти похитителя глины и его жертву по
результатам измерения вылепленных детьми брусков.
Дана одна или больше групп детей, перечисление которых заканчивается строкой, содержащей `-1`.
Каждая группа начинается со строки, содержащей `n` – число детей в группе. Дальше идут `n` строк с информацией
об учениках. Каждая строка содержит три положительных числа, представляющих собой размеры
получившегося бруска, и имя ребенка. В любой группе не меньше 2 и не больше 9 учеников.
Имя ребенка не более 8 букв. Миссис Терри выдает самое большее по 250 кубических единиц глины каждому ученику.
В группе находится ровно один похититель и один пострадавший.
Напечатайте одну строку для каждой группы, содержащую имена похитителя и его жертвы так, как показано в примере.
Пример ввода
3
10 10 2 Jill
5 3 10 Will
5 5 10 Bill
4
2 4 10 Cam
4 3 7 Sam
8 11 1 Graham
6 2 7 Pam
-1
Пример вывода
Bill Will
Graham Cam
3. Дважды два
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Для развития математических способностей у студентов, предлагается следующее упражнение. Дается список,
состоящий из положительных случайных неповторяющихся целых чисел. Длина списка от 2 до 15. Требуется сосчитать,
сколько в списке чисел, равных некоторому удвоенному числу из этого же списка.
Вы должны написать программу, которая поможет выставить студентам оценки. Эта программа должна просматривать
предлагаемые списки и выводить для каждого корректный ответ. Например, дан список
1 4 3 2 9 7 18 22
Ваша программа должна ответить 3, так 2 равно удвоенной 1, 4 равно `2\ *\ 2` и `18\ =\ 9\ *\ 2`.
Входной файл состоит из одного или более списков чисел. В одной строке содержится один список.
Каждый список содержит от 2 до 15 различных положительных целых. Все числа не превосходят 99.
Каждая строка завершается нулем, который не рассматривается как часть списка.
Строка с единственным числом `-1` означает конец файла. Ниже приводится пример, содержащий три отдельных списка.
Некоторые списки могут вообще не содержать удвоенных значений.
Выходной файл должен состоять из строк, по одной для каждого входного списка, содержащих количество чисел,
являющихся удвоенными значениями других.
Пример ввода
1 4 3 2 9 7 18 22 0
2 4 8 10 0
7 5 11 13 1 3 0
-1
4. Обычные билеты
Ограничения: время – 2s/4s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Питер любит теорию чисел. Поэтому он интересуется автобусными билетами.
Билет с числом длиной `2N` цифр является "интересным", если произведение первых `N` цифр этого числа равно произведению
последних `N` цифр. Другие билеты называются "обычными".
Питер нашел использованный билет в кармане. К сожалению, билет был прокомпостирован,
так что Питер не мог разобрать некоторые цифры. Он хотел узнать, является ли этот билет
"интересным" для него. Более того, он хотел узнать, как много различных "интересных" и "обычных" билетов
при компостировании могли дать этот билет.
Помогите Питеру найти ответы на его вопросы.
Первая строка входного файла содержит целое число `N` (`1\ ≤\ N\ ≤\ 9`). Следующая строка содержит номер билета.
Если некоторая цифра прокомпостирована, она помечается как "?", в противном случае она изображается как есть.
Первая строка выходного файла должна содержать число "интересных" билетов.
Вторая строка выходного файла должна содержать число "обычных" билетов.
Источник: ACM ICPC NEERC, Northern subregion 2003
5. Роботы
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Ваша компания продает роботов, которые могут подбирать мусор с полей после спортивных мероприятий и концертов.
Прежде чем робот назначается на работу, поле фотографируется с воздуха и на фотографию наносится сетка.
Каждая клетка сетки, содержащая мусор, помечается. Все роботы начинают свою работу с верхнего левого угла и заканчивают
движение в нижнем правом углу. Робот может двигаться только в двух направлениях: вправо и вниз.
При прохождении робота по клетке, содержащей мусор, он этот мусор будет собирать.
После того, как робот достигнет правого нижнего угла, он не может быть перенаправлен или повторно использован.
Так как ваши затраты прямо пропорциональны количеству роботов, задействованных в работе, вы заинтересованы в
нахождении минимального количества роботов, которые смогут очистить данное поле.
Например, рассмотрим карту поля, показанную на рисунке 1, с пронумерованными строками и столбцами.
Клетки, содержащие мусор, помечены буквой 'G'. По этой схеме роботы будут начинать работу с позиции 1,1 и
заканчивать в позиции 6,7.
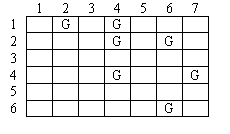 | 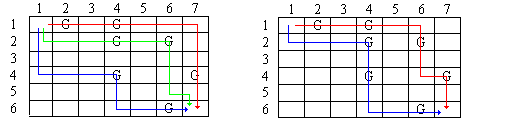 |
| Рис. 1. Карта поля | Рис. 2. Два возможных решения |
Рисунок 2 показывает два возможных решения. Второй из них предпочтительнее, поскольку использует двух роботов, а не трех.
Ваша задача – создать программу, которая будет определять минимальное количество роботов, необходимых для уборки
всего мусора с поля.
Во входном файле содержится одна или более карт поля, за которой следует строка, содержащая -1 -1, что означает конец
входных данных. Карта поля состоит из одной или более строк, каждая строка содержит одну клетку,
где содержится мусор. За картой поля следует строка, содержащая 0 0, означающая конец карты.
Каждое расположение мусора состоит из двух целых чисел: номер строки и столбца,
разделенные единственным пробелом. Строки и столбцы пронумерованы, как показано на рис. 1.
Расположения мусора будут заданы в отсортированном по строкам порядке.
Ни одна карта не может быть больше, чем 24 строки и 24 столбца.
В примере входного файла, показанном ниже, содержится две карты. Первая из них – карта поля с рис. 1.
Выходной файл состоит из одной строки для каждой карты, содержащей минимальное
количество роботов, необходимых для очистки соответствующего поля. Возможно пересечение
траекторий движения роботов по карте.
Пример ввода
1 2
1 4
2 4
2 6
4 4
4 7
6 6
0 0
1 1
2 2
4 4
0 0
-1 -1
6. Миномизация
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Разнообразные варианты игры "Сапер" существуют практически для всех платформ.
Руководитель вашей софтверной фирмы планирует создать еще одну ее версию, позиционируемую как игру для
начинающих геймеров. Ваша задача состоит в написании программы, которая по заданному игровому минному полю вычисляет
минимальное число незаминированных клеток, которые останутся закрытыми после работы такого неопытного игрока.
Подробные сведения об игре и программе приводятся ниже.
Поле для игры "Сапер" состоит из прямоугольной сетки, одна или более ячеек которой заминированы.
В начале игры все клетки поля закрыты. Цель игры состоит в том, чтобы открыть все незаминированные ячейки.
Если открывается ячейка с миной, то игра заканчивается и игрок проигрывает. Ячейка может находиться в одном из
трех состояний: закрыта, открыта/пустая или помечена флажком как заминированная.
Когда игрок открывает незаминированную клетку, в ней отображается число мин, спрятанных в соседних клетках.
Это число помогает игроку выяснить расположение мин. Соседними считаются клетки, образующие
квадрат `3\ times\ 3` с открываемой клеткой в центре. В зависимости от местоположения клетки она может иметь
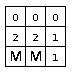
от 3 до 8 соседних ячеек. На рис. 1 показаны две мины с координатами (3,1) и (3,2) и число соседствующих мин для
всех оставшихся клеток.
Неопытный игрок, имея эту информацию, поступает следующим образом. Первым делом он выбирает одну ячейку из
полностью закрытого поля. Если там находится мина, игра заканчивается. Иначе, он открывает эту клетку и до
тех пор, пока возможно, применяет два следующих правила для разминирования оставшегося поля.
Пусть `(x,\ y)` – координаты открытой ячейки, и пусть `f`, `c` и `m` – число помеченных флажком, закрытых и
заминированных соседних с `(x, y)` клеток.
- Если `f\ =\ m`, тогда открыть все закрытые соседние с `(x,\ y)` клетки.
- Если `f\ +\ c\ =\ m` тогда все закрытые соседние с `(x,\ y)` клетки пометить флагом.
Отметим, что после успешно открытой первой клетки, неопытный игрок никогда не открывает и не помечает флагом ячейки,
кроме как в соответствии с правилами 1 и 2. Это означает, что он может зайти в тупик.
Когда такое происходит, игра останавливается. Никаких дополнительных предположений о расположении мин не делается,
никакие более сложные правила, позволяющие безопасно открыть оставшиеся клетки не применяются.
 |  |  |  |  |  |
| a) | b) | c) | d) | |
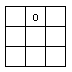
| Рис. 1 | Рис. 2 | Рис. 3 |
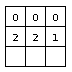
На рис. 2 показано использование этих правил для позиции на рис. 1.
Рис. 2a содержит позицию на доске после начального вскрытия клетки `(1,\ 2)`. Здесь можно применить правило 1,
поскольку (0 помеченных флагом = 0 заминированных соседних) и игрок открывает соседние клетки `(1,\ 1)`, `(1,\ 3)`,
`(2,\ 1)`, `(2,\ 2)` и `(2,\ 3)`, как показано на рис. 2b.
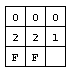
Далее игрок рассматривает ячейку `(2,\ 1)` и применяет правило 2 (0 помеченных флагом + 2 закрытых = 2 заминированных)
чтобы пометить ячейки `(3,\ 1)` и `(3,\ 2)` как заминированные. Результат приведен на рис. 2c.
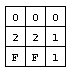
Окончательно, рассматривая клетку `(2,\ 3)`, игрок вновь применяет правило 1 и открывает ячейку `(3,\ 3)`, поскольку `(2,\ 3)`
соседствует ровно с одной миной, и ячейка `(3,\ 2)` уже помечена флажком. Теперь все ячейки без мин открыты,
игра завершается победой игрока.
Как было сказано выше, этих двух правил недостаточно, чтобы открыть целиком любое поле, начиная с любой клетки.
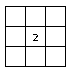
Вновь рассмотрим позицию на рис. 1. Если игрок начнет открывать поле с клетки `(2,\ 2)`, то возникнет ситуация
как на рис. 3. Игрок не сможет продвинуться дальше, поскольку ни правило 1, ни правило 2 не позволяют открыть
или пометить флажком ни одну из клеток. В этом случае игрок застопорился, имея шесть закрытых незаминированных клеток.
Вы должны написать программу, которая анализирует игровое поле и определяет наименьшее число незаминированных клеток,
которые возможно останутся закрытыми после того, как неопытный игрок выполнит вышеописанные действия.
Для игрового поля на рис. 1 верным ответом будет 0.
Входной файл содержит одно или более игровых полей, за которыми следует строка с двумя нулями.
Описание поля начинается с двух целых чисел `r` и `c` – число строк и столбцов поля; `r` и `c` всегда больше либо
равны 3. Число ячеек любого поля не больше 40.
Последующие данные являются графическим представлением игрового поля: латинская прописная буква 'M'
означает мину, и точка '.' означает пустую клетку. На любой доске всегда имеется хотя бы одна мина
и хотя бы одна пустая клетка.
Для каждого набора данных, выведите одну строку, содержащую наименьшее число закрытых незаминированных клеток
для этого поля.
Пример ввода
3 3
...
...
MM.
3 4
M.M.
.M.M
M.M.
7 5
.....
.....
MMM..
M.M..
MMM..
.....
.....
4 4
...M
....
....
M...
0 0
 Задачи районно-городских командных соревнований 2003
Задачи районно-городских командных соревнований 2003 Комбинаторика, теория Пойа
Комбинаторика, теория Пойа

 Преобразование или подсчет характеристики (например, сумма) заданной или вычисляемой последовательности
Преобразование или подсчет характеристики (например, сумма) заданной или вычисляемой последовательности


 Полный перебор
Полный перебор

 Динамическое программирование и запоминающие функции
Динамическое программирование и запоминающие функции

 Задачи на идею
Задачи на идею



 Моделирование
Моделирование








 Начало
Начало Соревнования
Соревнования