Методы уменьшения размера задачи

Методы уменьшения размера задачи основаны на использовании связи между решением данного экземпляра задачи и решением меньшего экземпляра той же задачи. Если такая связь установлена, ее можно использовать либо сверху вниз (рекурсивно), либо снизу вверх (без использования рекурсии). Имеется три основных варианта уменьшения размера:

• уменьшение на постоянную величину;
• уменьшение на постоянный множитель;
• уменьшение переменного размера.

При уменьшении на постоянную величину размер экземпляра задачи снижается на одну и ту же постоянную величину при каждой итерации алгоритма. Обычно эта величина равна единице, хотя встречается и снижение размера на два — в алгоритмах, которые по-разному работают для экземпляров задач четного и нечетного размера.

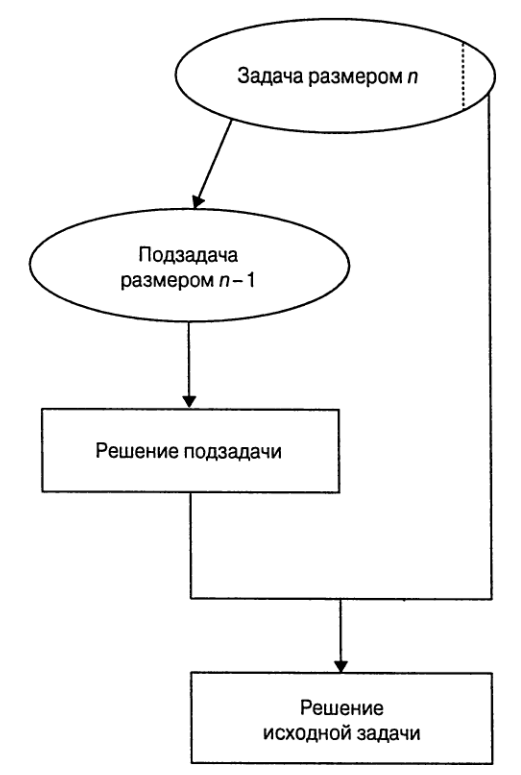
Рассмотрим в качестве примера задачу вычисления `a^n` для положительных целых показателей степени. Связь между решением экземпляра размером `n` и экземпляром размером `n-1` выражается очевидной формулой `a^n = a^{n-1}*a`. Таким образом, функция `f(n) = a^n` может быть вычислена либо "сверху вниз" с использованием рекурсивного определения
`f(a,n) = { (f(a,n-1)*a, "при " n>1),(a,"при " n=1) :}`
либо "снизу вверх" путем умножения `a` на себя `n-1` раз.

Уменьшение на постоянный множитель предполагает уменьшение размера экземпляра задачи при каждой итерации алгоритма на один и тот же множитель. В большинстве приложений этот множитель равен двум.

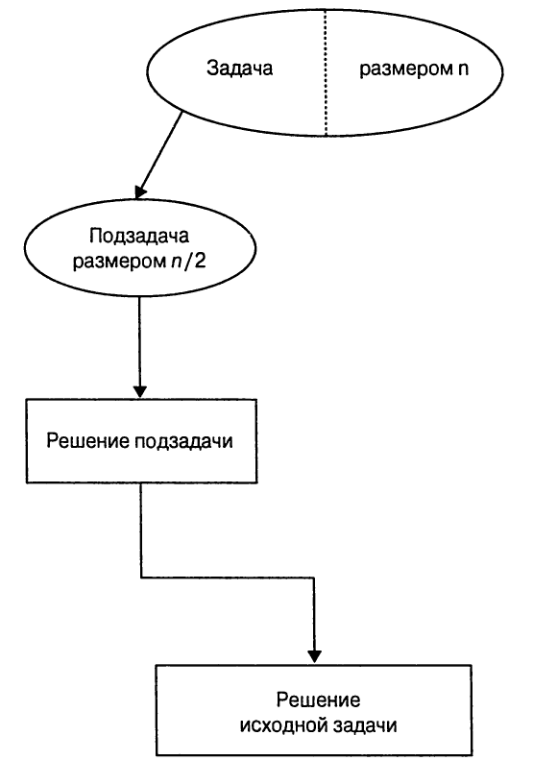
Для решения экземпляра задачи размером `n` — вычисления величины `a^n` — решается задача половинного размера, т.е. вычисляется значение `a^{n//2}`, которое связано с решением исходной задачи очевидным соотношением `a^n =(a^{n//2})^2`. Эта формула годится только для четных `n`. В случае нечетных `n` мы должны вычислить `a^{n-1}` по этой формуле, а затем умножить результат на `a`.
`f(a,n) = { ({:f(a,n//2)^2:},"при четном "n>1),({:f(a,(n-1)//2)^2*a:},"при нечетном "n>1),(a,"при "n=1):}`

Этот алгоритм принадлежит классу `O(log n)`, потому что при каждой итерации размер задачи снижается как минимум вдвое, ценой не более двух умножений. В общем случае этот вариант задачи реализуется через рекурсию, но если рекурсия является хвостовой (т.е. любой рекурсивный вызов является последней операцией перед возвратом из функции), то можно заменить рекурсию циклом while (см. бинарный поиск).

Уменьшение размера на постоянный множитель не эквивалентно методу декомпозиции, так как по методу декомпозиции нужно поделить на две подзадачи размером `|__n//2__|` и `|~n//2~|`:

`f(a,n) = { ({:f(a,|__n//2__|)*f(a,|~n//2~|):},"при "n>1),(a,"при "n=1):}`

Для нечетных `n` эти подзадачи не совпадают, а при рассмотрении дерева вызовов функции можно увидеть повторно решаемые подзадачи, В худшем случае эффективность алгоритма, основанного на методе декомпозиции, принадлежит классу `O(n)`.

При уменьшении переменного размера величина снижения размера задачи изменяется от итерации к итерации. Примером такого алгоритма может служить алгоритм Евклида для вычисления наибольшего общего делителя, основанного на формуле:
`gcd (m, n) = gcd (n, m mod n)`.

Хотя аргументы в правой части уравнения всегда меньше аргументов в левой части (как минимум, начиная со второй итерации алгоритма), они не меньше ни на постоянное значение, ни на постоянный множитель.

Задания для практики

1. Нарисуйте дерево вызовов функции возведения в степень `f(2,21)` по методу декомпозиции и по методу уменьшения на постоянный множитель. Сравните количество умножений.