Задания

1. Нарисуйте ДКА, проверяющий четность десятичного числа, заданного последовательностью цифр. OK: 4, 32, 5126. Error: 41, 7, 1023.

1. Нарисуйте ДКА, проверяющий, что в последовательности из 0 и 1 не более двух 1. OK: 010, 1100, 00. Error: 010110, 111.

1. Нарисуйте ДКА, проверяющий, что в последовательности из 0 и 1 нет двух 1 подряд. OK: 01, 100101, 00. Error: 010110, 11, 111.

1. Нарисуйте ДКА, проверяющий, что в последовательности из букв a и b есть обе буквы. OK: ab, baab, aaabaa. Error: aaaa, b, bb.

2. Напишите программу для машины Тьюринга, которая в последовательности из 0 и 1 переставляет все цифры 1 в конец. 10100 должно превратиться в 00011.

2. Напишите программу для машины Тьюринга, которая в последовательности из 0 и 1 убирает первый 0, если он есть, сдвигая остальные цифры вперед. 101001 должно превратиться в 11001, 111 остается без изменений.

2. Напишите программу для машины Тьюринга, которая в последовательности из 0 и 1 оставляет только последний символ, заменяя остальные на □ (пустая ячейка). 10100 должно превратиться в □□□□0.

2. Напишите программу для машины Тьюринга, которая в последовательности из a,b,c заменяет последний символ последовательности на первый. abcb должно превратиться в abca, bcc - в bcb, cbaa - в cbac.

3. Определите нормальный алгоритм Маркова для выполнения следующей задачи. Убрать начальные 0 в непустой строке из 0 и 1 (нули после первой 1 не трогать).

3. Определите нормальный алгоритм Маркова для выполнения следующей задачи. Если непустая строка из букв a,b,c содержит ровно три символа, заменить её на yes, иначе на no

3. Определите нормальный алгоритм Маркова для выполнения следующей задачи. Заменить непустую строка из букв a,b,c на количество различных символов в ней (цифру 1, 2 или 3)

3. Определите нормальный алгоритм Маркова для выполнения следующей задачи. Если в строке из букв a,b,c есть символ a, заменить строку на yes, иначе на no

5. Разработайте алгоритм решения следующей задачи и опишите его на естественном языке или псевдокоде. Предположим, на плоскости находится `n` точек, заданных их координатами `(x,y)`. Определите, лежат ли все точки на одной и той же окружности?

5. Разработайте алгоритм решения следующей задачи и опишите его на естественном языке или псевдокоде. Предположим, на плоскости находится `n` точек, заданных их координатами `(x,y)`. Определите, лежат ли все точки на одной и той же прямой?

5. Разработайте алгоритм решения следующей задачи и опишите его на естественном языке или псевдокоде. Дан набор из `n` натуральных чисел, необходимо проверить, что это перестановка чисел от 1 до `n`, т.е. каждое число от 1 до `n` входит в набор ровно один раз.

5. Разработайте алгоритм решения следующей задачи и опишите его на естественном языке или псевдокоде. Дан набор из `n` различных целых чисел, необходимо определить, сколько в этом наборе пар целых чисел, равных по модулю, но противоположных по знаку.

a) `sqrt{n^3+10 n^2}`

a) `n sqrt{5 n^2-n}`

a) `n/{sqrt{n+5}}`

a) `root{3}{4 n^5+n}`

b) `"lg"(n^3+n^2)+n "lg"\ n`

b) `log_2(10 n^2+n)`

b) `n^2* "lg"\ n+5 n* "ln"(n^10+10 n)`

b) `log_2^2(n/10)+3*log_2(n^10)`

c) `3^{n//2}+2^{n-2}`

c) `n^{100}+10^n`

c) `(n+1)^{n-2}+10^{2n}`

c) `3^{2n-10}+2^{3n+10}`

`sum_{i=0}^{n-1} (i^2+1)^2`

`sum_{i=1}^{n} 2/{i+1}`

`sum_{i=2}^{n-1} "lg"\ i^2`

`sum_{i=0}^{n-1}sum_{j=0}^{i-1} (i+j)`

`x(n)=3x(n-1) " для " n>1, x(1)=2`

`x(n)=x(n-1)+n " для " n>0, x(0)=1`

`x(n)=x(n//2)+n " для " n>1, x(1)=1` (найдите решение для `n=2^k`)

`x(n)=x(n//3)+1 " для " n>1, x(1)=1` (найдите решение для `n=3^k`)

9. Детерминант (определитель) матрицы `A` размером `n xx n` обозначаемый как `"det" A`, может быть определен следующим образом. При `n = 1` он равен `a_{11}`. При `n > 1` его можно вычислить по приведенной ниже рекурсивной формуле
`"det" A =sum_{j=1}^n (-1)^{j-1} a_{1,j} M_{1,j}`
В этой формуле `a_{1,j}` — это элемент первой строки и `j`-ro столбца, а `M_{1,j}` — детерминант матрицы размером `(n-1) xx (n-1)`, полученной из исходной матрицы `A` путем вычеркивания первой строки и `j`-ro столбца.
а) Напишите рекуррентное уравнение для количества операций умножения, выполняемых при вычислении детерминанта по описанной выше рекурсивной формуле.
б) Не решая это рекуррентное уравнение, что вы можете сказать о его порядке роста в сравнении с факториалом `n!` ?

9. Перманентом матрицы `A` размером `n xx n` называется число
`"perm" A =sum_{pi in P_n} prod_{i=1}^n a_{i,pi_i}`
где `P_n` — множество всех перестановок размером `n`, `a_{i,j}` -- элемент матрицы
а) Напишите выражение для количества операций умножения.
б) Определите порядок роста.

9. Перманент матрицы `A` размером `n xx n` может быть вычислен по формуле Райзера
`"perm" A =(-1)^n sum_{S sube {1,..,n} } (-1)^{|S|} prod_{i=1}^n sum_{j in S} a_{i,j}`
где `S` — подмножество `1..n`, `|S|` -- его размер, `a_{i,j}` -- элемент матрицы
а) Напишите выражение для количества операций сложения.
б) Определите порядок роста.

9. Для вычисления чисел Бернулли существует следующая рекуррентная формула:
`B_0=1`,
`B_n=(-1)/(n+1) sum_{k=1}^n С_{n+1}^{k+1} B_{n-k} где C_n^k -- число сочетаний из`n`по`k`и может быть вычислено за`2*min(k,n-k)`умножений. а) Напишите рекуррентное уравнение для количества операций умножения, выполняемых при вычислении`B_n`. б) Не решая это рекуррентное уравнение, что вы можете сказать о его порядке роста в сравнении с факториалом`n!` ?

Размер	1000	2000	3000	4000	5000	6000	7000	8000	9000	10000
Количество	11966	24303	39992	53010	67272	78692	91274	113063	129799	140538

Размер	1000	2000	3000	4000	5000	6000	7000	8000	9000	10000
Количество	17567	40418	59443	82271	112380	129589	162165	185410	204471	223634

Размер	1000	2000	3000	4000	5000	6000	7000	8000	9000	10000
Количество	97891	404167	869884	1557900	2408419	3452824	4686428	6132158	7747612	9552964

Размер	1000	2000	3000	4000	5000	6000	7000	8000	9000	10000
Количество	19812	54036	98635	151019	210857	264985	322918	407240	475274	546964

11. Сколько сравнений символов сделает алгоритм поиска подстроки, основанный на грубой силе, для шаблона 00001 в тексте, состоящем из 1000 нулей?

11. Сколько сравнений символов сделает алгоритм поиска подстроки, основанный на грубой силе, для шаблона abcd в тексте, состоящем из 1000 повторений abc: abcabcabc...?

11. Сколько сравнений символов сделает алгоритм поиска подстроки, основанный на грубой силе, для шаблона 000 в тексте, состоящем из 1000 повторений 001: 001001001001...?

11. Сколько сравнений символов сделает алгоритм поиска подстроки, основанный на грубой силе, для шаблона abc в тексте, состоящем из 1000 повторений aba: abaabaaba...?

`T(n) = 4T (n//2) + n, T(1) = 1`.

`T(n) = 4T (n//2) + n^2, T(1) = 1`.

`T(n) = 4T (n//2) + n^3, T(1) = 1`.

`T(n) = 3T (n//2) + n^2, T(1) = 1`.

13. Триомино — элемент мозаичного заполнения в форме L, образованный тремя квадратами шахматной доски. Задача состоит в покрытии триомино шахматной доски размером `2^n xx 2^n` с одной вырезанной в произвольном месте клеткой. Триомино должны покрывать все клетки, за исключением вырезанной, без пропусков и перекрытий. Разработайте декомпозиционный алгоритм для решения этой задачи.

13. Лабиринт строится следующим образом. Лабиринт `L(k)` имеет размер `2^k` и строится из 4 лабиринтов `L(k-1)`. Две верхних части лабиринта `L(k)` повторяют структуру `L(k-1)`, часть в левом нижнем углу — структуру `L(k-1)`, повернутого по часовой стрелке, а часть в правом нижнем углу — структуру `L(k-1)`, повернутого против часовой стрелки. На рисунке показаны планы лабиринтов `L(1), L(2), L(3)`.

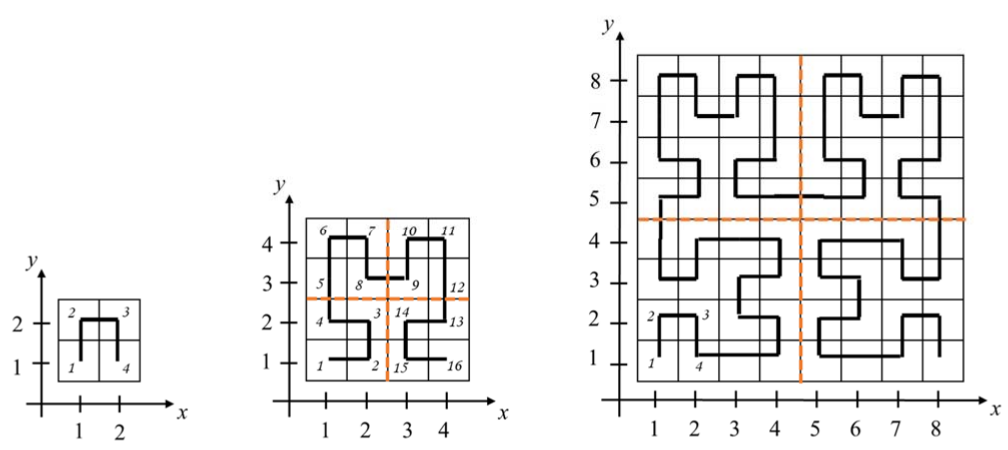
Аня зашла в лабиринт, сделала несколько шагов и теперь не знает, где она находится. Разработайте алгоритм методом уменьшения на постоянный множитель для решения задачи об определении координат Ани `(x,y)` в лабиринте по размеру лабиринта `k` и количеству сделанных ею шагов `M <=4^k`.

13. Определим множества `K_i` рекуррентно. Пусть `K_0 = [0,1]`. Разделим сегмент `[0,1]` на три части точками 1/3 и 2/3 и удалим из него интервал `(1//3,2//3)`. Получим множество `K_1`, состоящее из двух оставшихся сегментов `[0,1//3]` и `[2//3,1]`. Каждый из них разделим на три части (точками 1/9 и 2/9 для первого сегмента, и точками 7/9 и 8/9 – для второго) и удалим средние интервалы `(1//9,2//9)` и `(7//9,8//9)`. Таким образом получаем множество `K_2`, и т.д. Пусть мы построим множество `K_i`. Поделим каждый оставшийся сегмент из `K_i` на 3 части и удалим из этих сегментов средние интервалы. Получим, таким образом, из `K_i` множество `K_{i+1}`.
Разработайте алгоритм методом уменьшения на постоянный множитель для решения задачи об определении, принадлежит ли точка с координатой `a//b` множеству `K_n`.

13. На рисунке показан процесс рисования снежинки Коха 0, 1, 2 и 3-го порядка.

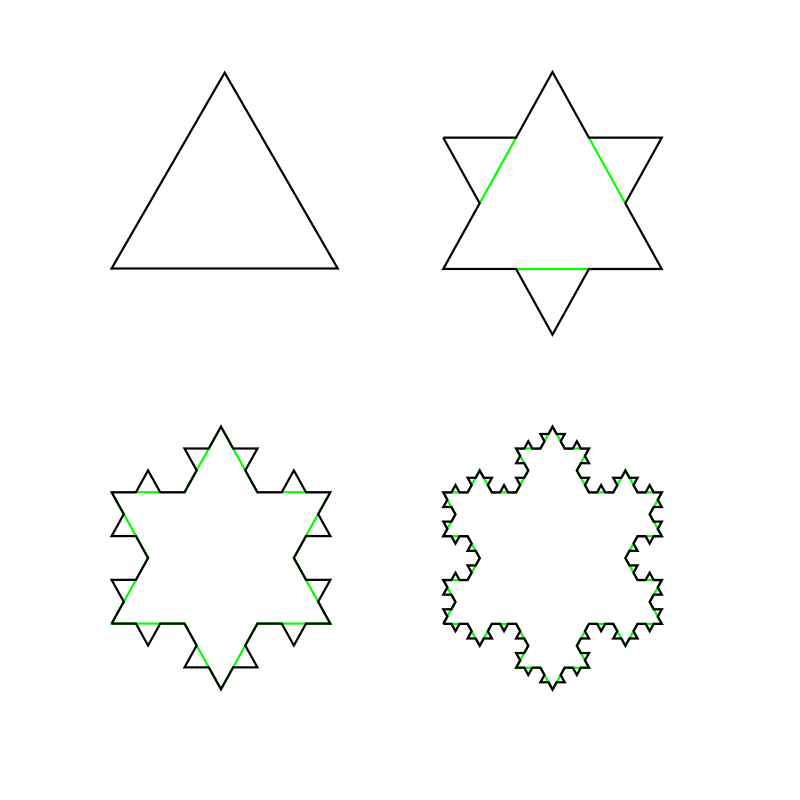
Разработайте декомпозиционный алгоритм для рисования снежинки Коха `k`-го порядка с помощью черепашьей графики с командами "повернуть на `x` градусов" и "вперед на `x` сантиметров".

14. Множество хранится в виде массива (порядок элементов в множестве не важен; множество, представленное списком {2,3,1,5} и списком {1,5,2,3}, являются одним и тем же множеством). Как удалить `i`-й элемент множества за `Theta(1)`? Здесь `i` - номер элемента, а не значение.

14. Предположим, нужно найти число в связном списке, состоящем из `n` элементов. Упростится ли решение, если список будет отсортирован? Объясните ответ.

14. Сравните эффективность алгоритмов поиска индекса минимального значения в связном списке и в массиве.

14. Сравните эффективность алгоритмов перестановки элементов списка в обратном порядке для связного списка и для массиве.

15. Оцените, во сколько раз быстрее в среднем будет выполняться успешный бинарный поиск в отсортированном массиве из 100000 элементов по сравнению с последовательным поиском.

15. Оцените, во сколько раз быстрее в среднем будет выполняться успешный бинарный поиск в отсортированном массиве из 10000 элементов по сравнению с последовательным поиском.

15. Оцените, во сколько раз быстрее в среднем будет выполняться успешный бинарный поиск в отсортированном массиве из 1000 элементов по сравнению с последовательным поиском.

15. Оцените, во сколько раз быстрее в среднем будет выполняться успешный бинарный поиск в отсортированном массиве из 1000000 элементов по сравнению с последовательным поиском.

16. Необходимо переставить элементы в массиве из `n` действительных чисел, чтобы все отрицательные числа предшествовали положительным, при этом порядок среди положительных и среди отрицательных чисел не важен. К какой известной из лекций задаче эту задачу можно привести? Выбранный алгоритм должен быть эффективен как в смысле времени работы, так и в смысле используемой памяти.

16. Пусть `A ={a_1, a_2,..., a_n}` и `B ={b_1, b_2,...,b_n}` — два множества чисел. Рассмотрим задачу поиска их пересечения, т.е. множества `C` всех чисел, которые входят как в `A`, так и в `B`. Повысит ли предварительная сортировка множеств `A` и `B` эффективность поиска пересечения? Идея какого алгоритма из лекций поможет решить эту задачу?

16. Пусть `A ={a_1, a_2,..., a_n}` и `B ={b_1, b_2,...,b_n}` — два множества чисел. Рассмотрим задачу поиска их объединения, т.е. множества `C` всех чисел, которые входят как в `A`, так и в `B`. Повысит ли предварительная сортировка множеств `A` и `B` эффективность поиска объединения? Идея какого алгоритма из лекций поможет решить эту задачу?

16. Оцените, какое количество поисков следует выполнить, чтобы оправдать время, затраченное на предварительную сортировку массива из `10^3` элементов, если она выполняется при помощи сортировки слиянием, а поиск — с использованием бинарного поиска. В качестве основной операции рассматриваем сравнение. Cчитаем, что поиск элементов, о которых заведомо известно их наличие в массиве, выполняется в половине случаев.

17. Пусть для списка вашей группы была построена хеш-таблица размером `m=33` для хеш-функции, которая возвращает номер первой буквы фамилии. Найдите наибольшее количество сравнений ключей при успешном поиске в полученной таблице; найдите среднее количество сравнений ключей при успешном поиске в полученной таблице.

17. Пусть для списка вашей группы была построена хеш-таблица размером `m=33` для хеш-функции, которая возвращает номер первой буквы имени. Найдите наибольшее количество сравнений ключей при успешном поиске в полученной таблице; найдите среднее количество сравнений ключей при успешном поиске в полученной таблице.

17. Если хеш-функция распределяет ключи равномерно по всем ячейкам таблицы размером `m`, то вероятность попадания двух или более ключей в одну ячейку таблицы при распределении `n` ключей равна `1-{m!}/{m^n(m-n)!}`. Используем в качестве хеш-функции номер дня года (от 1 до 365) из даты рождения для группы из `n=35` человек. Найдите вероятность совпадения дня рождения.

17. Если хеш-функция распределяет ключи равномерно по всем ячейкам таблицы размером `m`, то вероятность попадания двух или более ключей в одну ячейку таблицы при распределении `n` ключей равна `1-{m!}/{m^n(m-n)!}`. Используем в качестве хеш-функции номер дня года (от 1 до 365) из дня рождения для группы из `n=33` человек. Найдите вероятность совпадения дня рождения.

Количество способов `K(i,j,k)` добраться шахматным конем до клетки `(i,j)` за `k` ходов из клетки `(1,1)` на шахматной доске. Выразите `K(i,j,k)` через решения для меньших значений `k`.

Дан ряд штабелей из ящиков, в `i`-м штабеле `H_i` ящиков. Можно добавлять и убирать ящики. Необходимо так изменить ряд штабелей, чтобы высоты соседних штабелей отличались не более чем на 1, а высота первого и последнего штабеля ряда не превосходила 1. Пусть `K(i,h)` - минимальное количество изменений в штабелях c 1 по `i`-й требуемых высот, а в `i`-ом штабеле высоты `h`. Выразите `K(i,h)` через решения для меньших значений.

Найти разбиение `N` школьников на группы в форме квадратов. Количество групп в разбиении должно быть как можно меньше. Выразите минимальное количество групп `G(i)` для `i` школьников через решения для меньших значений.

Найти разбиение `N` школьников на группы в форме квадратов, среди которых нет двух одинаковых по количеству. Количество групп в разбиении должно быть как можно больше. Выразите максимальное количество групп `G(i,s)` для `i` школьников c использованием квадратов `s xx s` или меньших через решения для меньших значений.

19. Для танца "Ручеек" `N` мальчиков и `N` девочек нужно разделить на пары из мальчика и девочки. Нужно разбить детей на пары так, чтобы суммарная разница в росте по всем парам была минимальна. Какой жадный алгоритм нужно применить? Докажите, что он будет давать оптимальный результат.

19. Недавно стало известно, что в романе "Война и мир" Л.Н.Толстой зашифровал много важных предсказаний, касающихся событий 20 и 21 века. Например, на первой странице первого тома можно обнаружить слова, произнесенные Нилом Армстронгом, когда он ступил на Луну: "One small step for man, one giant leap for mankind". Для этого нужно взять 22 букву из 1 строки (O), затем 17 и 24 буквы из 2 строки (N и E), затем... Укажите жадный алгоритм, который находит способ прочтения заданного текста в некоторой последовательности букв. Начинать можно с любой буквы последовательности, затем нужно переходить на любую букву, номер которой в последовательности строго больше номера предыдущей буквы. Последовательность выбранных букв должна совпасть с заданным текстом. Докажите, что алгоритм найдет результат, если такая последовательность существует.

19. В аудитории стоит ряд из `N` столов. За некоторыми из них сидят студенты. Петя сидит за первым столом, Маша - за `N`-м. Петя хочет незаметно от преподавателя передавать и получать сообщения от Маши. Для незаметной передачи разница между номерами столов не должна превышать 2, т.е. записка может быть переброшена со стола `i` на стол `j` только если `|i-j| <= 2` и за обоими столами сидят студенты. Для успешной передачи сообщений Петя может пригласить на помощь еще несколько студентов, чтобы они сели за пустующие столы. Нужно определить минимальное количество студентов, которых нужно посадить за пустующие столы для незаметной передачи сообщений. Заданы номера столов, за которыми сидят студенты. Укажите жадный алгоритм, который указывает за какие столы нужно посадить еще студентов. Докажите, что алгоритм дает минимальное количество дополнительных студентов.

19. Два игрока по очереди берут по одной карточке из общей кучи. На каждой карточке написано некоторое целое число, которое может быть как положительным, так и отрицательным. Карточки лежат числом вверх. Игрок, взявший карточку, может либо забрать её себе, либо отдать сопернику. В начале игры карточек на руках ни у кого нет. Когда игроки разберут все карточки, игра заканчивается и игроки считают сумму чисел на своих карточках. Игроки стараются максимизировать разность между количеством своих очков и количеством очков соперника. Укажите жадный алгоритм, который обеспечивает максимально возможную разность между очками первого игрока и его соперника (второй игрок будет действовать оптимальным образом).

Определение того, является список из `n` целых чисел перестановкой (содержит все числа от 1 до `n` ровно один раз).

Проверка связности графа, представленного матрицей смежности.

Генерация всех перестановок из `n` элементов.

Поиск моды (наиболее частого элемента) массива.

21. Укажите пример P и NP задачи для графов.

21. Укажите пример P и NP задачи в теории чисел. (Примеры из области обычной арифметики не указывать!)

21. Укажите пример P и NP задачи для систем неравенств (или уравнений).

21. Укажите пример P и NP задачи для булевых формул.

22. Нарисуйте дерево пространства состояний для задачи о пяти ферзях на доске `5 xx 5` для получения одного полного решения.

22. Нарисуйте дерево пространства состояний для задачи о подмножестве с заданной суммой для получения одного полного решения. `S = {2,4,7,9,10,15}` и `d = 21`.

22. Нарисуйте дерево пространства состояний для задачи о назначениях с матрицей стоимости
`C=((6,5,7,10),(9,12,9,6),(15,5,8,11),(8,11,14,8))`

22. Нарисуйте дерево пространства состояний для задачи о рюкзаке.
`W=14`

Предмет	Вес	Стоимость
1	4	30
2	7	28
3	9	54
4	5	15
5	2	5

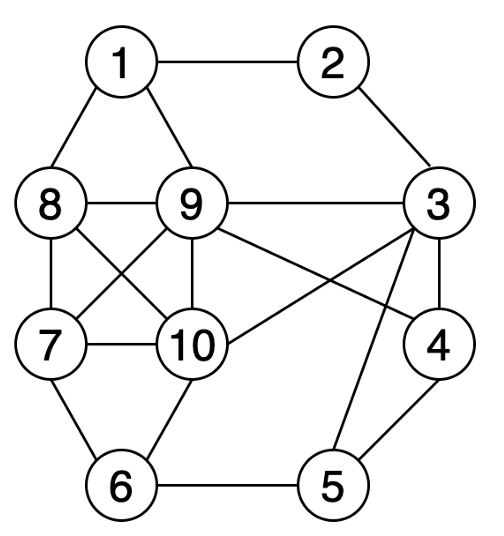
23. Раскрасьте граф, показанный ниже, с помощью следующего алгоритма. Назовем "степенью насыщенности" вершины количество различных цветов, используемых ее соседями.
1. Найдем неокрашенную вершина в графе с наибольшей степенью насыщения. В случае равенства выбираем среди них вершину, у которой наибольшее количество неокрашенных соседей.
2. Окрасим её в наименьший доступный цвет, не использовавшийся для окраски соседей.
3. Если остались неокрашенные вершины, перейдем к шагу 1.
Сравните результат работы этого алгоритма с результатами алгоритма, который выполняет обход графа в ширину, начиная с вершины 1, и раскрашивает вершину в наименьший доступный цвет, не использовавшийся для окраски соседей.

23. В алгоритме первого подходящего для задачи об упаковке корзин каждый предмет в порядке поступления помещаем в первую корзину, в которую он может поместиться; если таких корзин нет - помещаем его в новую корзину и добавляем ее в список корзин. Алгоритм первого подходящего с убыванием начинается с сортировки предметов в невозрастающем порядке по их размерам, после чего работает так же, как и алгоритм первого подходящего. Примените оба алгоритма к экземпляру задачи `S={0.4, 0.7, 0.2, 0.1, 0.5, 0.6, 0.25, 0.45, 0.8, 0.15}`, объем корзины считается равным 1. Результаты какого алгоритма лучше?

23. В алгоритме первого подходящего для задачи об упаковке корзин каждый предмет в порядке поступления помещаем в первую корзину, в которую он может поместиться; если таких корзин нет - помещаем его в новую корзину и добавляем ее в список корзин. Алгоритм наилучшего подходящего по убыванию начинается с сортировки предметов в невозрастающем порядке по их размерам, а среди корзин выбираем корзину в которой после упаковки остался наименьший свободный объём, достаточный для размещения предмета; если таких корзин нет - помещаем его в новую корзину и добавляем ее в список корзин. Примените оба алгоритма к экземпляру задачи `S={0.4, 0.7, 0.2, 0.1, 0.5, 0.6, 0.25, 0.45, 0.8, 0.15}`, объем корзины считается равным 1. Результаты какого алгоритма лучше?

23. Раскрасьте граф, показанный ниже, с помощью следующего алгоритма.
1. Отсортируйте вершины графа в порядке уменьшения их степени (при совпадении степени по возрастанию номеров).
2. При обходе вершин в этом порядке раскрашивайте вершину в наименьший доступный цвет, не использовавшийся для окраски соседей.
Сравните результат работы этого алгоритма с результатами алгоритма, который выполняет обход графа в глубину, начиная с вершины 1, и раскрашивает вершину в наименьший доступный цвет, не использовавшийся для окраски соседей.

24. Воспользуйтесь формулой трапеций при `n = 4` для приближенного вычисления указанного ниже определенного интеграла. Найдите ошибку усечения для каждого интервала, сравнивая с точным значением, вычисляемым по формуле.
`int_0^1 x^2 dx`

24. Воспользуйтесь формулой прямоугольников при `n = 4` для приближенного вычисления указанного ниже определенного интеграла. Найдите ошибку усечения для каждого интервала, сравнивая с точным значением, вычисляемым по формуле.
`int_1^3 1/x dx`

24. Примените метод деления пополам для поиска корня уравнения `x^3+x-3=0` с абсолютной ошибкой меньшей `10^{-2}`.

24. Примените метод тернарного поиска для нахождения значения минимума функции `f(x)=х^3-cos(х-1)` на интервале `[0,1]` с абсолютной ошибкой меньшей `10^{-2}`.

25. Для решения системы из `n` линейных уравнений методом исключения Гаусса требуется выполнить `2*n^3//3` операций умножения или вычитания. Вычисления для double выполняются с ошибкой округления `epsilon=10^{-15}`. Оцените точность решения для системы из `n=100` уравнений.

25. Студент проверяет алгоритм тернарного поиска, выполняя поиск минимума для функции `"cosl"(x)` на интервале [3, 4]. С какой точностью может быть найдена точка минимума `x` (приближенно равная `pi`), если ошибка при вычислении функции `"cosl"(x)` равна `epsilon=10^{-18}`.

25. Студент проверяет алгоритм тернарного поиска, выполняя поиск минимума для функции `f(x)=(x-C)^2+1`, где `C` - некоторая константа. С какой точностью может быть найдена точка минимума `x` (приближенно равная `C`), если ошибка при вычислении функции `f(x)` равна `epsilon=10^{-15}`.

25. Интеграл функции `f(x)` на интервале `[a,b]` методом прямоугольников вычисляется через сумму значений функции `f(x)` в `n` точках. При этом ошибка приближения для одного прямоугольника примерно равна `1/n^2`, то есть при увеличении `n` точность результата возрастает. С другой стороны при большом `n` начинают влиять ошибки округления при вычислении функции и сложении. Вычисления для double выполняются с ошибкой округления `epsilon=10^{-15}`. Для какого `n` точность результата будет максимальна?