7866.png
ЧЕЛЯБИНСК,ЮУРГУ,ИЕТН

Назад

images/home.png Начало
images/balloon.gif Соревнования
2008
Задачи командного чемпионата

Подразделы

Другие разделы

Дата и время

21/12/2024 23:28:10

Авторизация

Имя:
Пароль:
Зарегистрироваться
Восстановить пароль
 

printВсе задачи

printЗадачи

A. Краски

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Фирма "All Colors Mixing" предлагает большой ассортимент красок по каталогу. Чтобы не хранить много красок в каждом магазине, большинство красок изготавливается на месте при поступлении заказа путем смешивания из нескольких базовых красок. Пропорция красок, необходимая для получения нужного оттенка, указывается в каталоге. Например, для получения сиреневой краски нужно смешать красную, синюю и белую краски в пропорции 1:2:3. Аппарат для смешивания красок может отмерять только выражаемые целыми числами объемы базовых красок. Поэтому, если покупателю необходимо 10 мл сиреневой краски, необходимо изготовить 12 мл краски, смешав 2 мл красной, 4 мл синей и 6 мл белой краски.
Напишите программу, вычисляющую минимальное количество краски, которое необходимо изготовить для выполнения заказа.
Первая строка ввода содержит одно целое число `N` (`1\ ≤\ N\ ≤\ 5`) – количество базовых красок для получения нужного цвета. Вторая строка ввода содержит `N` целых чисел в диапазоне от 1 до 1000, разделенных пробелами – пропорция смешивания базовых красок. Третья строка содержит одно целое число `V` (`10\ ≤\ V\ <\ 10^9`) – количество краски, необходимое покупателю.
Вывести одно целое число – минимальное количество краски, которое нужно изготовить для выполнения заказа покупателя.

Пример ввода

3
1 2 3
10

Пример вывода

12

B. Машины на полке

Ограничения: время – 2s/4s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Сэм хочет расставить свою коллекцию моделей машин на полке в несколько рядов таким образом, чтобы все ряды имели одинаковую длину. Машины разделяются на нескольких типов. Машины одного типа имеют одинаковую длину.
Напишите программу, определяющую, как нужно расставить машины.
В первой строке ввода содержатся два целых числа – количество различных типов машин `N` (`1\ ≤\ N\ ≤\ 5`) и число рядов `M` (`1\ ≤\ M\ ≤\ 20`). Во второй строке содержатся `N` целых положительных чисел, разделенных пробелами – количества машин каждого типа. Общее количество машин не превышает 100. В третьей строке содержатся `N` целых чисел, разделенных пробелами – длины машин каждого типа в диапазоне от 1 до `10^5`.
Вывести `M` строк, содержащих по `N` чисел – для каждого ряда указывается число машин каждого типа, поставленных в соответствующий ряд. Можно вывести любое из решений, удовлетворяющее условиям. Если размещение коллекции в `M` рядов одинаковой длины невозможно, вывести сообщение "IMPOSSIBLE".

Пример ввода

3 2
2 3 2
15 10 7

Пример вывода

2 0 1
0 3 1

C. Строительство дорог

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Король Флатландии решил направить свою страну по пути научно-технического прогресса и повелел построить `K` железных дорог таким образом, чтобы из любого города страны можно было проехать до любого другого по железной дороге прямо или с пересадками через другие города. Железнодорожные компании, заинтересованные в финансировании, предложили министру транспорта откат в случае принятия их предложений. Хитрый министр решил построить дороги таким образом, чтобы не только обеспечить выполнение приказа короля, но и получить максимальный доход.
В первой строке ввода содержатся три целых числа, разделенных пробелами – количество городов в стране `N` (`1\ <\ N\ ≤\ 30000`), число предложений от компаний `M` (`N-1\ ≤\ M\ ≤\ 10^5`) и количество дорог `K` (`N-1\ ≤\ K\ ≤\ M`). Далее следует `M` строк, содержащих по три целых числа – номера городов `a_i` и `b_i` (`1\ ≤\ a_i\ <\ b_i\ ≤\ N`), между которыми предлагается построить дорогу, и величина отката `c_i` (`0\ ≤\ c_i\ ≤\ 10^9`). Пары городов в списке предложений не повторяются.
Вывести одно целое число – максимальный доход министра. Если выполнить приказ короля невозможно, вывести число `-1`.

Пример ввода

4 6 5
1 2 200
1 3 100
1 4 150
2 3 90
2 4 180
3 4 120

Пример вывода

750

D. Прокладка кабеля

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

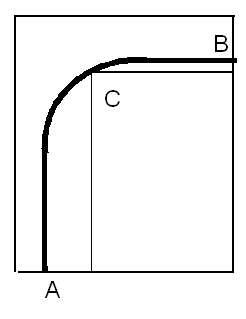
Необходимо проложить кабель для скоростной передачи данных из лаборатории к компьютерам. Кабель выходит из стены лаборатории, затем идет прямо по коридору, на углу поворачивает по кругу на 90 градусов и затем идет прямо к стене компьютерной комнаты (см. рис). Для уменьшения потерь информации радиус поворота кабеля должен быть как можно больше, насколько позволяет форма коридора. Напишите программу, вычисляющую максимальный радиус поворота при прокладке кабеля.
Ввод содержит в первой строке 6 целых чисел `x_A`, `y_A`, `x_B`, `y_B`, `x_C`, `y_C` (`0\ ≤\ x_A\ ≤\ x_C\ ≤\ x_B\ ≤\ 10000`, `0\ ≤\ y_A\ ≤\ y_C\ ≤\ y_B\ ≤\ 10000`), разделенных пробелами – координаты точки A, в которой кабель выходит из стены лаборатории, координаты точки B, в которой кабель входит в стену компьютерной комнаты, и координаты угла коридора С. В точках A и B кабель должен быть перпендикулярен стене.
Вывести одно число с точностью `10^{-5}` – максимальный радиус поворота.

Пример ввода

10 0 90 110 30 100

Пример вывода

50.00000

E. Игра

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Сэм и Макс играют в следующую игру. Игра ведется с помощью листа бумаги, разделенного на `N`x`M` клеток. Некоторые клетки окрашены в черный цвет. В процессе игры лист разрезается на части. Игроки ходят по очереди. Ход заключается в следующем. Игрок берет одну из образовавшихся в процессе игры частей и вырезает из нее столбец или строку (т.е. полоску клеток `n`x1 или 1x`m`), содержащую хотя бы одну черную клетку. Вырезанный столбец или строка уничтожается и больше в игре не используется. При выполнении хода выбранная игроком часть может разделиться на две или может быть уничтожена, если она состояла из одной строки или столбца. Проигрывает тот, кто не может сделать очередной ход.
Напишите программу, которая вычисляет, кто из игроков побеждает на заданном начальном листе при безошибочной игре обоих участников.
В первой строке ввода содержатся два целых числа `N` и `M` (`1\ ≤\ N,\ M\ ≤\ 20`) – размеры листа. Далее следует `N` строк, в каждой строке `M` символов – раскраска клеток листа. Черная клетка обозначается символом '#', белая – символом '.'.
Вывести одно целое число – номер игрока, который выиграет на заданном начальном листе.

Пример ввода

3 2
##
..
#.

Пример вывода

2

F. Аппроксимация

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

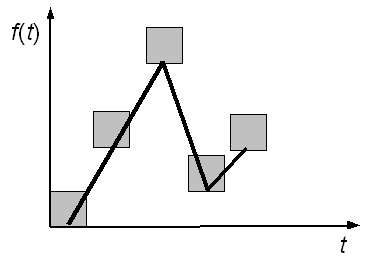
В результате измерений была получена зависимость некоторого параметра от времени. Значение параметра измерялось каждую единицу времени, при измерении выполнялось преобразование аналогового значения в цифровую форму и дробная часть результата измерений отбрасывалась. Например, если в момент времени `i` было получено цифровое значение `y_i` для параметра, это означает, что реальное значение `f_i` измеряемого параметра было `y_i\ ≤\ f_i\ <\ y_i\ +\ 1`.
Необходимо описать зависимость параметра от времени с помощью кусочно-линейной аппроксимации, разбив интервал времени измерений на наименьшее число участков. Границы участков должны быть целыми числами. В пределах каждого участка для аппроксимирующей прямой `F(t)\ =\ a*t\ +\ b` должно выполняться условие `y_i\ ≤\ F(i)\ <\ y_i\ +\ 1`.
В первой строке ввода содержится одно целое число `N` (`2\ ≤\ N\ ≤\ 100`) – число измерений. Во второй строке содержится `N` целых чисел, разделенных пробелами, в диапазоне от 0 до 255 – результаты измерений.
В первой строке вывести одно число `K` – минимальное число участков. Далее следует `K` строк, в каждой строке должно быть по четыре числа – начало и конец участка `s_i`, `t_i` (целые, `t_{i-1}\ =\ s_i\ <\ t_i`, `t_K\ =\ N`, `s_1\ =\ 1`), и коэффициенты `i`-й прямой `a_i`, `b_i` с точностью `10^{-6}`.

Пример ввода

5
1 3 5 2 3

Пример вывода

3
1 3 2.000000 -1.000000
3 4 -3.000000 14.000000
4 5 1.000000 -2.000000

G. Play with Cubes

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (1)

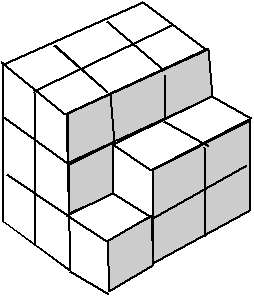
The first line of the input file contains a single integer `N` (`1\ ≤\ N\ <\ 10^9`) representing the number of unit cubes.
Write to the output file minimal number of unit cubes which need adding to `N` cubes so it must be possible to assemble a entire cube from all unit cubes.

Sample Input

23

Sample Output

4

H. Another Cipher Method

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Sam and Max are passing messages with each other at school hours. In order to the teacher can't read the intercepted message, Sam proposed to write all words in reverse order but keep the right order of letter cases. A word is defined as a consecutive sequence of letters (upper and/or lower case). Other symbols are written as usual.
This cipher method is too complex, and so Max requested for deciphering program.
The input file contains the encoded message (up to 100 lines with length up to 50 symbols).
Write to the output file the decoded message.

Sample Input

Tel em wonk tuoba eht 22dn fo Rebmevon
sa ylkciuq sa uoy NAC.

Sample Output

Let me know about the 22nd of November
as quickly as you CAN.

I. Цифры

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Сэм составляет число, записывая слева направо последовательность ненулевых цифр. При добавлении каждой цифры он проверяет, чтобы у получившегося числа не было простых делителей больших некоторого числа `K`. Сэм получал разные последовательности в зависимости выбора цифры на очередном шаге, но всегда после нескольких шагов получалось число, к которому он не мог добавить новой цифры. Например, для `K\ =\ 7` у Сэма получались числа 81, 256 или 324. Сэма интересует, какое наибольшее число он может получить для заданного `K`.
В первой строке ввода содержится одно целое число `K` (`2\ ≤\ K\ ≤\ 250`).
Вывести наибольшее число, которое может получиться у Сэма для заданного `K`.

Пример ввода

250

Пример вывода

1449777425

J. Машины в коробке

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

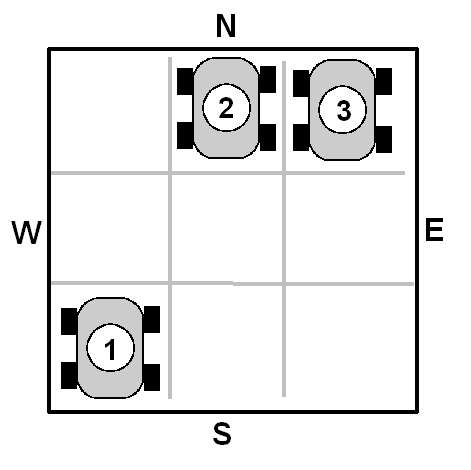
Макс хранит свои радиоуправляемые машины в большой коробке размером 3x3, в которой может поместиться вплотную 3 ряда по 3 машины. Начальное расположение машин в коробке неизвестно. С помощью пульта управления Макс может двигать машины в коробке в 4-х направлениях в соседнюю позицию. Если на пути движения машины находится стенка или другая машина, машина не выполняет команду и сообщает звуковым сигналом об ошибке.
Напишите программу, которая определяет расположение машин в коробке после выполнения серии команд.
В первой строке ввода содержатся два целых число – количество машин в коробке `N` (`1\ ≤\ N\ ≤\ 8`) и количество команд `K` (`1\ ≤\ K\ ≤\ 100`). Далее следует `K` строк, каждая строка содержит одну команду в формате `"idf"`, где `i` (`1\ ≤\ i\ ≤\ N`) – номер машины, `d` – направление движения машины с номером `i`, задается символами 'N' (север), 'S' (юг), 'E' (восток), 'W' (запад), `f` – результат выполнения команды, символ '+' (машина выполнила команду) или '-' (машина наткнулась на препятствие).
Вывести 3 строки, содержащих по 3 символа – предполагаемое конечное расположение машин в коробке. Клетка с машиной содержит номер машины, а пустая – символ '.'. Если входным данных соответствует несколько возможных расположений, вывести одно из них (любое).

Пример ввода

3 4
1N+
2S+
3N-
1N+

Пример вывода

1.3
.2.
...
Примечание: Предполагаемое начальное расположение показано на рисунке.

K. Гонка преследования

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

В гонке преследования участники стартуют в таком порядке и с такими интервалами, с какими они пришли на финиш в спринте. Участник, пришедший первым к финишу по результатам спринта, стартует первым. Участник, показавший время в спринте на `t` секунд больше победителя, стартует на `t` секунд позже первого участника. Чтобы во время старта спортсмены не мешали друг другу, участники с близким временем должны стартовать по разным дорожкам. Дорожка становится доступной для старта очередного участника через `D` секунд.
Напишите программу, вычисляющую по результатам спринта минимальное количество стартовых дорожек в гонке преследования.
В первой строке ввода содержатся два целых числа – число участников `N` (`1\ ≤\ N\ ≤\ 1000`) и интервал времени в секундах между стартами участников по одной дорожке `D` (`1\ ≤\ D\ ≤\ 100`). Далее следует `N` строк, `i`-я строка содержит время финиша `i`-го участника в спринте в формате `h`:`"mm"`:`"ss"`, где `h` (`0\ ≤\ h\ <\ 20`) – часы, `"mm"` (`00\ ≤\ "mm"\ ≤\ 59`) – минуты, а `"ss"` (`00\ ≤\ "ss"\ ≤\ 59`) – секунды. В спринте используется раздельный старт участников с интервалом в 1 минуту, т.е. `i`-й участник стартует в момент времени (`i-1`):00, результат участника вычисляется как разница между временем старта и временем финиша. Время финиша у всех участников больше времени старта.
Вывести одно число – минимальное число стартовых дорожек в гонке преследования.

Пример ввода

3 10
0:09:15
0:10:00
0:11:05

Пример вывода

2
loading