Кроссворд

Крисс-кросс, или… ЭВРИСТИЧЕСКОЕ СОСТАВЛЕНИЕ ГОЛОВОЛОМКИ

Многие считают кроссворды слишком трудной головоломкой, потому что отгадать слово им не под силу. Но вписывать буквы в клетки нравится. Для подобных людей существует более простая головоломка — крисс-кросс.

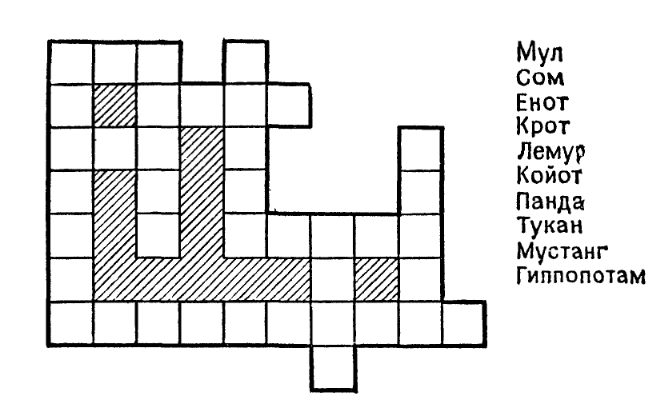
Каждый крисс-кросс состоит из списка слов, разбитых для удобства на группы в соответствии с длиной и упорядоченных по алфавиту внутри каждой группы, а также из схемы, в которую нужно вписать слова. Схема подчиняется тому же правилу, что и в кроссворде, — в местах пересечения слова имеют общую букву, однако номера отсутствуют, поскольку слова известны заранее, требуется лишь вписать их в нужные места. Обычно в схемах крисс-кросса гораздо меньше пересечений по сравнению с кроссвордами, а незаполняемые клетки не заштриховываются, если это не приводит к путанице. Крисс-кросс всегда имеет единственное решение, в котором используются все перечисленные слова. Пример головоломки, правда очень маленький, приведен на рис. Заметьте, что длина слова служит важным ключом к разгадке.

Тема. Напишите программу, читающую список слов и строящую для этого списка правильную схему крисс-кросса. Представьте заполненную схему как доказательство того, что она правильная. Возможно, хотя и маловероятно, что для данного списка слов не существует решения (как и в кроссворде, схема должна быть связной). Ваша программа должна сообщать о всех неудачах при построении схемы и о всех ситуациях, нарушающих однозначность (таких, например, как наличие повторяющихся слов). Попутно решите еще одну задачу — получите красивый графический вывод.

Указания исполнителю. Качество схем крисс-кросса пропорционально их «связанности», т. е., чем теснее в среднем слова переплетены с соседями, тем интереснее головоломка. Связанность можно измерять по-разному: как отношение площади схемы к площади наименьшего объемлющего прямоугольника; как среднее число пересечений на слово; как среднее число пересечений на букву; как минимальное число пересечений на слово. При генерации головоломок крисс-кросс для массовых изданий использовалась коммерческая программа, но головоломки получались неинтересные — слишком длинные и извилистые. Когда ваша программа заработает, позаботьтесь об увеличении связанности. Предложенная задача — классическая для метода перебора с возвратами. Начните с вписывания слов в фиксированную схему, пока в списке есть подходящие слова. Когда они кончатся, вернитесь на шаг назад, удалив последнее вписанное слово, и попытайтесь вписать другое слово. Необходимо разработать эвристику для выбора очередного кандидата из списка неиспользованных слов. Контроль однозначности должен включать проверку того, что в схеме нельзя поменять местами никакие два слова равной длины. Достаточна ли такая проверка? Нет ли более изящной? Полное алгоритмическое решение, максимизирующее связанность, несомненно, представит значительный теоретический интерес.