НачалоПодразделы
Другие разделы
| 790. Word Ladder |
| 791. Bonus Word |
| 792. Contest |
| 794. Escape |
| 795. Settling Salesman Problem |
| 796. Space |
| 797. Herbert |
Дата и время
17/11/2024 01:16:04
793. Cycling
Задача
Олимпиадные задачи на английском языке| 08/02/2008 | Тренировка (задачи Benelux APC preliminary 2007) (D) |
| 11/07/2013 | Лето 2013-8 (D) |
Ограничения: время – 5s/10s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
You want to cycle to a programming contest. The shortest route to the contest might
be over the tops of some mountains and through some valleys. From past experience you
know that you perform badly in programming contests after experiencing large differences
in altitude. Therefore you decide to take the route that minimizes the altitude difference,
where the altitude difference of a route is the difference between the maximum and the
minimum height on the route. Your job is to write a program that finds this route.
You are given:
- the number of crossings and their altitudes, and
- the roads by which these crossings are connected.
Your program must find the route that minimizes the altitude difference between the
highest and the lowest point on the route. If there are multiple possibilities, choose the
shortest one.
For example:
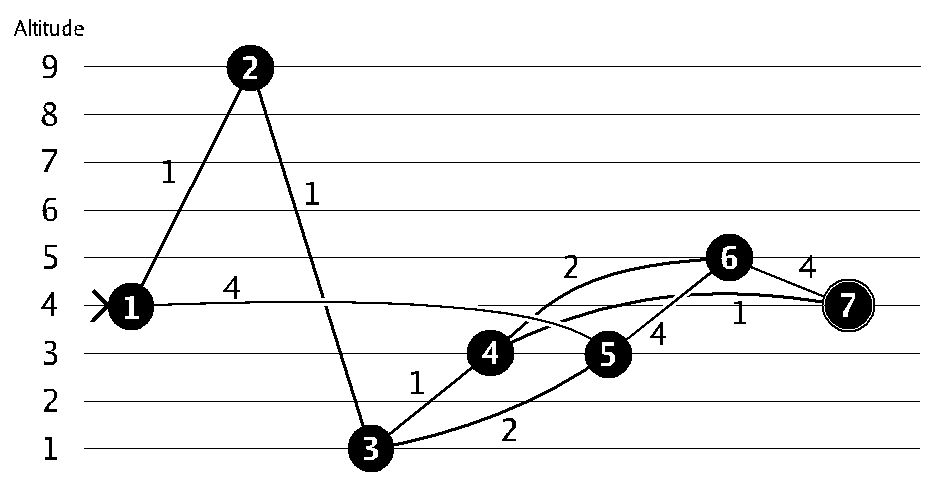
In this case the shortest path from 1 to 7 would be through 2, 3 and 4, but the altitude
difference of that path is 8. So, you prefer to go through 5, 6 and 4 for an altitude difference
of 2. (Note that going from 6 directly to 7 directly would have the same difference in
altitude, but the path would be longer!)
Input
On the first line an integer `t` (`1\ ≤\ t\ ≤\ 100`): the number of test cases. Then for each test
case:
- One line with two integers `n` (`1\ ≤\ n\ ≤\ 100`) and `m` (`0\ ≤\ m\ ≤\ 5\ 000`): the number of crossings and the number of roads. The crossings are numbered `1…n`.
- `n` lines with one integer `h_i` (`0\ ≤\ h_i\ ≤\ 1\ 000\ 000\ 000`): the altitude of the `i`-th crossing.
- `m` lines with three integers `a_j` , `b_j` (`1\ ≤\ a_j\ ,\ b_j\ ≤\ n`) and `c_j` (`1\ ≤\ c_j\ ≤\ 1\ 000\ 000`): this indicates that there is a two-way road between crossings `a_j` and `b_j` of length `c_j`. You may assume that the altitude on a road between two crossings changes linearly.
You start at crossing 1 and the contest is at crossing `n`. It is guaranteed that it is possible to reach the programming contest from your home.
Output
For each testcase, output one line with two integers separated by a single space:
- the minimum altitude difference, and
- the length of shortest path with this altitude difference.
Sample input
1 7 9 4 9 1 3 3 5 4 1 2 1 2 3 1 3 4 1 4 7 1 1 5 4 5 6 4 6 7 4 5 3 2 6 4 2
Sample output
2 11
